가장 큰 정사각형 : https://school.programmers.co.kr/learn/courses/30/lessons/12905#
Problems

Solve
첫번째 풀이에서는 특정 지점인 (i,j)에서 정사각형을 이루는 길이를 하나씩 늘려가며 해당 길이가 정사각형을 이루는지 확인하는 과정을 반복하여 최대의 길이를 찾아 반환하는 풀이를 생각했지만, 효율성에서 시간초과가 되어 다른 방법을 찾아보게 되었습니다.
위에 풀었던 방법이 맞긴 한데, 효율성에서 시간 초과를 하는것을 보고 각 좌표에서 해당 정사각형에 대한 정보를 가지는 DP로 접근해보기로 했습니다.
온전히 제 힘으로는 해결하지는 못했고 중간에 다른 분의 풀이법을 참고하였습니다.
먼저 특정 위치 (i,j)에서 정사각형 여부를 확인하기 위해, (i-1,j), (i,j-1), (i-1, j-1)의 값을 비교합니다. 만약 비교하는 세 값 중 가장 작은 값이 0이 있다면 해당 위치의 값은 정사각형이 될 수 없습니다. 즉, 이 경우는 (i,j)는 1
비교하는 세 값이 0이 아닌 값을 가진다면, 일단은 정사각형을 만족하는 조건을 가지기 때문에 세 값중 가장 작은 값에 +1을 해줍니다.
직접 예시를 들어보도록 하죠.
int[][] board = {{1,0,1,1,1},{0,1,1,1,1},{1,1,1,1,1},{0,0,0,1,0}} 이 주어졌다고 하겠습니다.
그렇다면
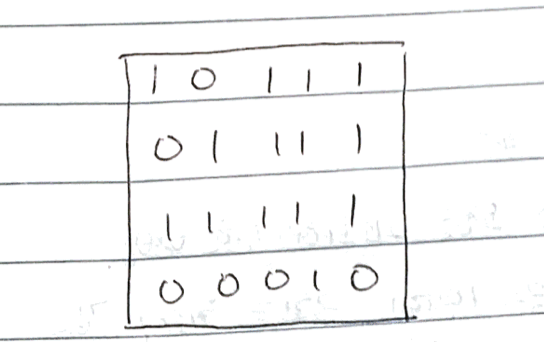
이러한 board가 생깁니다.
이를 (i-1,j-1), (i-1,j), (i,j-1) 3값을 비교해서 가장 작은 값에 +1을 해준게 (i,j)의 값이라 하였습니다.
그러기 위해서는 DP를 사용해야하는데, 만약 (0,0)이라면..? 해당 값도 비교해 주기 위해 int[][] dp = new int[H+1][W+1]로 놓고 구현하겠습니다.
dp를 만든다면 아래와 같습니다.
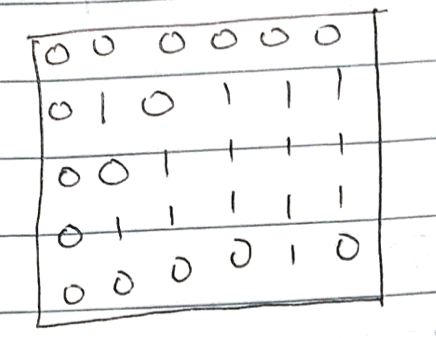
그리고 (0,0)의 dp를 알기 위해 dp에서는 각각 +1씩 해주어서 저장해주어야합니다. 그렇다면 dp[1][1]의 값을 구하기 위해 (0,0)은 0, (0,1)은 0, (1,0)은 0으로, 세 값 중 0을 포함하기 때문에 dp[1][1]의 값은 1을 가지게 됩니다. (가장 작은 값 + 1이기 때문에 1이기도 합니다.)
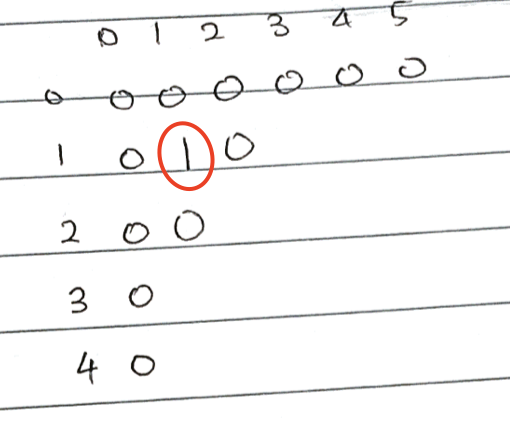
다음으로 (1,3)인 경우를 보겠습니다.
board[1][3]의 dp를 구하기 위해 dp[2][4]의 값을 구해야합니다. 그렇다면 (1,3), (1,4), (2,3)의 값을 비교해야하고 그 중 최소값은 1이므로 dp[2][4]는 2를 가지게 됩니다.

그렇다면 마지막으로 (2,4)의 경우를 보겠습니다.
board[2][4]의 dp를 구하기 위해서 (2,4), (2,5), (3,4)를 비교하고 최소값이 2이므로 dp[3][5]는 3의 값을 가지게 됩니다.
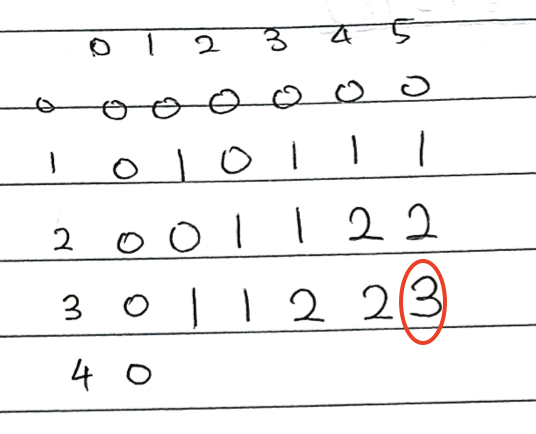
이 과정을 반복한 후, dp에서 가장 큰 값이 board에서 가지는 가장 큰 정사각형의 길이가 됩니다.
이렇게 하면 (i,j)에서 정사각형을 확인하기 위해 모든 (i,j)부터 끝까지 좌표를 확인하지 않아도 되어, O(N^2)으로 문제를 풀 수 있었습니다.
Code
class Solution
{
int W; //board 가로 길이
int H; //board 세로 길이
int[] dy = {-1,-1,0}; //위, 대각선, 왼쪽
int[] dx = {0,-1,-1}; //위, 대각선, 왼쪽
public int solution(int[][] board){
H = board.length;
W = board[0].length;
int[][] dp = new int[H+1][W+1];
//board에서 1을 가지는 좌표에 대해서만 dp를 설정합니다.
//0인 값은 어차피 0을 가집니다.
for(int i=0;i<H;i++){
for(int j=0;j<W;j++){
if(board[i][j]==1){
setDp(board, dp, i,j);
}
}
}
//dp에서 가장 큰 값 구하기
int answer = 0;
for(int i=1;i<H+1;i++){
for(int j=1;j<W+1;j++){
answer = Math.max(answer, dp[i][j]);
}
}
return (int)(Math.pow(answer,2));
}
public void setDp(int[][] board, int[][]dp, int y, int x){
int min = Integer.MAX_VALUE;
/*
위, 좌측 대각선, 왼쪽 좌표의 값을 비교하여 가장 작은 값을 찾는다.
그리고 dp[y+1][x+1]에 가장 작은 값에 +1을 하여 갱신한다.
*/
for(int d=0;d<3;d++){
int ny = y+dy[d];
int nx = x+dx[d];
min = Math.min(min, dp[ny+1][nx+1]);
}
dp[y+1][x+1] = min+1;
}
}Result
DP로 접근하긴 했지만, dp값을 구하는 식을 찾는게 어려웠다. 접근법은 빠르게 다가갔지만 풀이가 조금 오래걸린 문제
