경주로 건설 : https://programmers.co.kr/learn/courses/30/lessons/67259
Problem


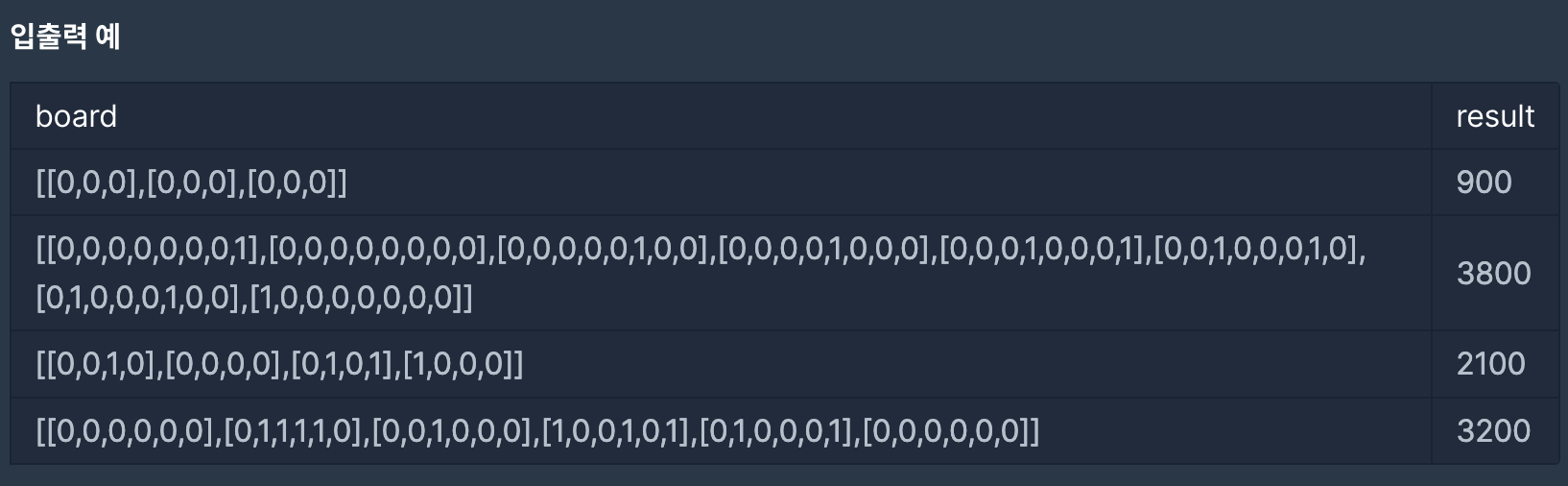
Solve
2차원 배열로 해결하려다 안되서 다른 분들의 코드를 보고 해결했다.
3차원 배열을 사용하는걸 보고 전에 백준에서 풀어봤던 유형이라 바로 풀수 있었다.
3차원 배열을 distanceBoard[y좌표][x좌표][방향] 으로 생각하고 푸는것이 문제의 핵심이다.
그리고 다른 BFS문제와 다르게 방문했던 좌표에 다시 방문할 수 있는데, 방문하려는 좌표가 이전에 방문했던 좌표이면 기존의 최소 비용보다 방문하려는 도로의 비용이 같거나 저렴할때 다시 방문할수 있다.
예를 들어보자
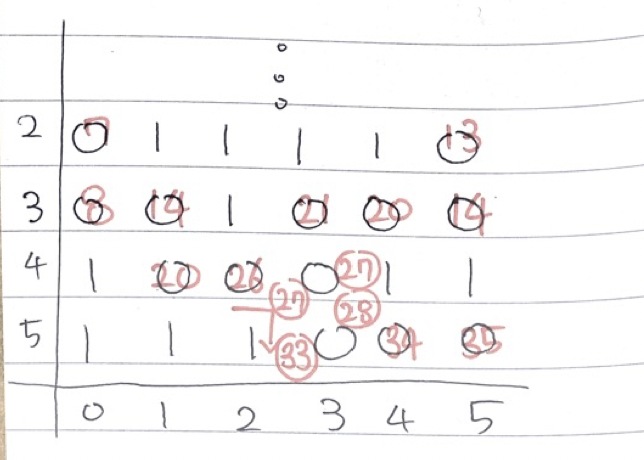
위의 그림과 같이 26(100)의 비용을 가지고 동쪽으로 직진 이동하는 도로(4,2)와 21(100)의 비용을 가지고 코너 이동하는 도로(3,3)가 같은 지점(4,3)에서 만났을 때 동쪽에서 직진 이동해온 결과(4,2)가 먼저 저장되어있다고 해보자.
그렇다면 이후에 접근하는 21의 비용을 가진 코너 이동하는 도로(3, 3)는 (4,2)도로가 이미 방문 해있기 때문에 접근 할수 없다.
하지만 결과론적으로 21의 비용을 가진 코너 이동하는 도로(3,3)로 계산한 비용이 최소비용이다.(21->27->28->34->35)
그렇기 때문에 방문은 했지만 기존 비용과 접근하는 비용을 비교하는 조건이 필요한것이다.
2차원 배열에서 방향과 위의 조건을 가지고 구현했을때 해결하지 못한 케이스이다.
이때 3차원 배열을 사용하게 된다면 distanceBoard[4][2][동쪽]=26, distanceBoard[3][3][서쪽]=21이 저장되어 있고 두 도로가 만나는 지점인 (4,3)은 distanceBoard[4][3][동쪽] = 27, distanceBoard[4][3][남쪽] = 27이 저장되어 따로따로 저장되게 된다.
그 후 남쪽으로 이동할때 distanceBoard[5][3][남쪽]에 distanceBoard[4][3][동쪽]값과 distanceBoard[4][3][남쪽]값을 비교해주고 더 작은 값을 갱신해준다.(앞으로 동선이 겹치기 때문에 최소 거리를 가지는 값을 저장해주는것)
비용 계산을 모두 마쳤다면 distanceBoard[N-1][N-1][동,서,남,북] 4가지를 모두 비교해서 가장 작은 값을 가지는 비용을 반환하면 된다.
Code
import java.util.Queue;
import java.util.LinkedList;
class Solution {
int N;
int cost;
//방향을 포함하는 3차원 배열
int[][][] distanceBoard;
//좌표 방문여부
boolean[][][] visit;
//위, 왼쪽, 아래, 오른쪽
int[] dy = {-1, 0, 1, 0};
int[] dx = {0, -1, 0, 1};
public int solution(int[][] board) {
N = board.length;
distanceBoard = new int[N][N][4];
visit = new boolean[N][N][4];
cost = Integer.MAX_VALUE;
//BFS
build(board);
//distanceBoard에서 맨 끝에 있는 좌표의 상하좌우 값을 모두 비교
for(int i=0;i<4;i++){
//특정 방향으로 마지막 좌표에 도달하지 못했을 경우 무시해준다(0값이기 때문)
if(distanceBoard[N-1][N-1][i] == 0) continue;
cost = Math.min(cost,distanceBoard[N-1][N-1][i]);
}
return cost;
}
void build(int[][] board){
Queue<Road> queue = new LinkedList<>();
queue.offer(new Road(0,0,0,-1));
//출발점 방문 갱신
visit[0][0][0] = true;
visit[0][0][1] = true;
visit[0][0][2] = true;
visit[0][0][3] = true;
while(!queue.isEmpty()){
Road r = queue.poll();
//마지막 좌표에 도달했다면 종료
if(r.y == N-1 && r.x == N-1){
continue;
}
//상하좌우 이동
for(int i=0;i<4;i++){
int ny = r.y+dy[i];
int nx = r.x+dx[i];
//이동할 좌표가 배열 범위를 벗어나지 않고 1이 아닌 값
if(ny>=0 && nx>=0 && ny<N && nx<N && board[ny][nx] != 1){
int newCost = r.cost;
//직진
if(r.distance == -1 || r.distance == i){
newCost += 100;
}
//코너
else{
newCost += 600;
}
//방문하려는 좌표가 방문한적이 없거나
//방문은 했지만 해당 방향으로 방문한 기존 비용보다 방문하는 도로의 비용이 같거나 저렴하다면 방문
if(!visit[ny][nx][i] || distanceBoard[ny][nx][i]>=newCost){
distanceBoard[ny][nx][i] = newCost;
visit[ny][nx][i] = true;
queue.offer(new Road(ny,nx,newCost,i));
}
}
}
}
}
class Road{
int y;
int x;
int cost;
int distance;
public Road(int y, int x, int cost, int distance){
this.y = y;
this.x = x;
this.cost = cost;
this.distance = distance;
}
}
}Result
(1트) 백트래킹을 이용해서 도면(board), y축, x축, 방향을 재귀함수의 argument로 주고 구현을 했었는데 시간초과가 발생했다.
(2트) BFS를 이용해 위와 유사하게 구현, 시간초과
(3트) 다른 분의 코드를 참고하여 BFS를 이용해 방문여부(visit)와 접근하려는 위치의 최소 비용과 접근하는 비용 비교를 통해 구현했다. 2021년 8월30일에 추가된 테스트케이스(25번)에서 막혔다.
(4트) 이전에는 기존에 2차원 배열(board)를 그대로 사용했다면, 이번에는 3차원배열(board[y축][x축][방향])을 이용해 3트에 구현했던 방식을 토대로 구현하였다.
4트째 문제를 해결하고보니 이전 백준에서 풀어봤던 유형인것같다. 3차원배열을 사용한 유형과 4차원배열을 사용한 유형까지 풀었던것같은데 몇달이 지나서 기억이 안났던것같다.. 그 문제 찾아서 다시 리마인드 해볼 필요가 있을것 같다.
Reference
https://moonsbeen.tistory.com/11
https://programmers.co.kr/questions/21325
(위의 참고자료는 3트때 참고했던 자료)
