프로그래머스 - 합승 택시 요금

합승 택시 요금 : https://programmers.co.kr/learn/courses/30/lessons/72413

---

Problems

---

Solves

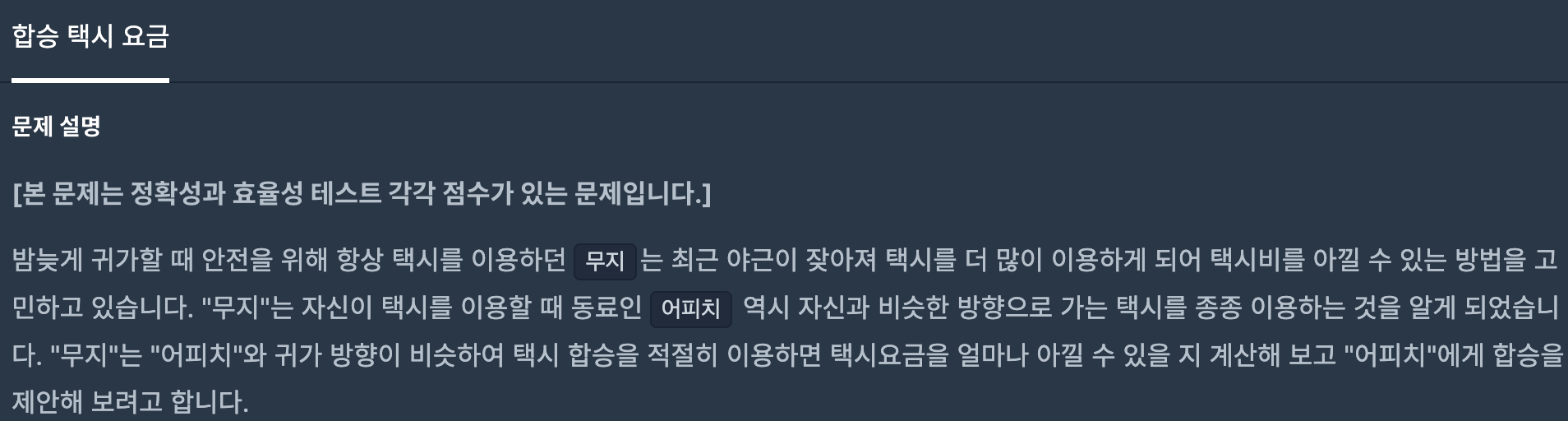
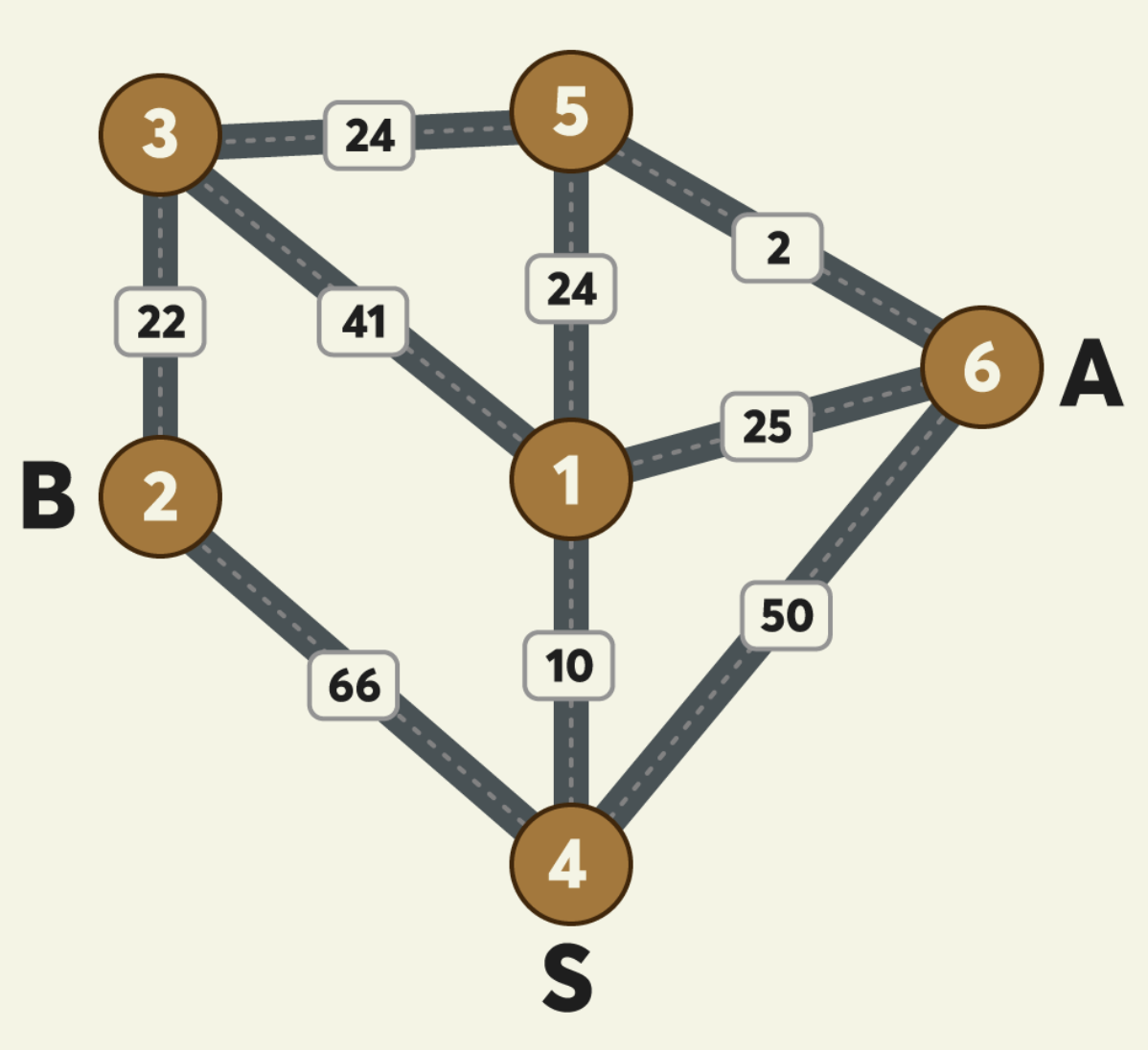
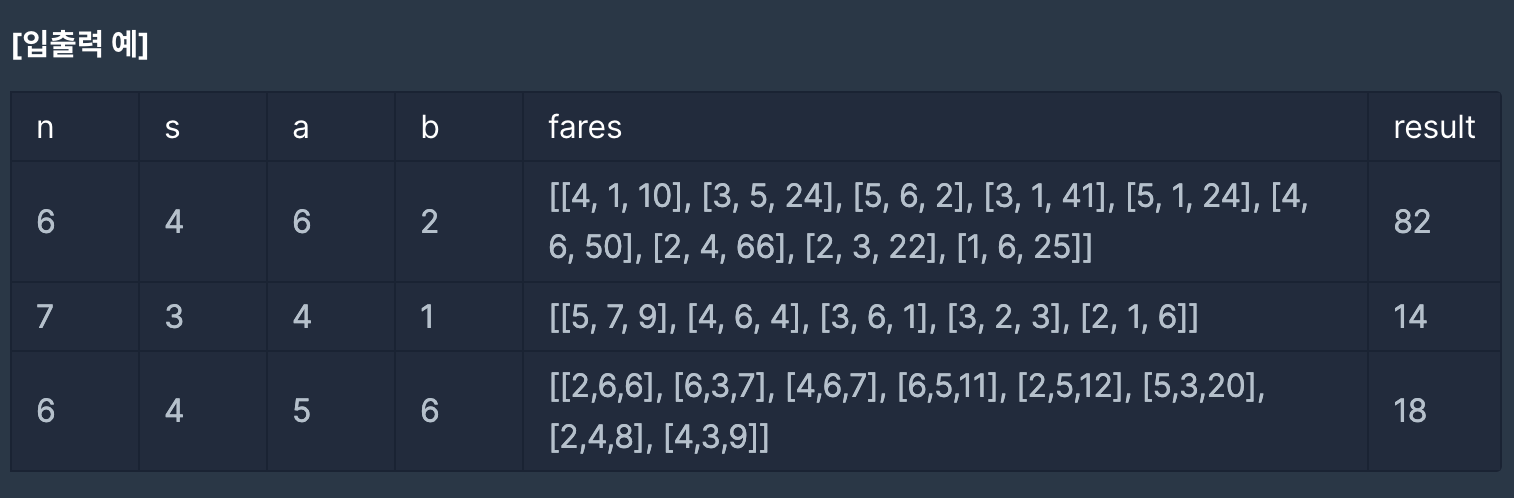
시작점 S에서 각각 A와 B로 가는 최소 비용을 구하는 문제.
그래프의 최소 거리(비용)을 구하는 문제이고 시작점이 있어서 다익스트라 알고리즘을 활용해서 풀수 있겠지만, 특정 지점까지 함께 갔다가 나눠서 각자의 목적지까지 가는 예시와 그래프의 크기가 최대 25인것을 보고 플로이드 와샬로 풀면 되겠구나 생각을 했다.
(플로이드 와샬 풀이 : https://velog.io/@hyunjong96/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-%EC%88%9C%EC%9C%84)

문제 풀이 순서는 아래와 같다.

1. 플로이드 와샬 알고리즘을 이용해 모든 정점에서 모든 정점까지의 그래프의 가중치를 갱신해준다.
2. 시작점 S부터 특정지점 K를 거쳐 목적지 A,B를 가는 최소 비용을 구한다.

---

Code

import java.util.Arrays;
class Solution {
    public int solution(int n, int s, int a, int b, int[][] fares) {
        int INF = 100000000;
        int[][] map = new int[n+1][n+1];
        //그래프 무한대 값을 나타내는 INF로 초기화
        for(int i=0;i<=n;i++){
            for(int j=0;j<=n;j++){
                map[i][j] = INF;
            }
            map[i][i] = 0;
        }
        
        for(int[] fare : fares){
            int c = fare[0];
            int d = fare[1];
            int f = fare[2];
            
            map[c][d] = f;
            map[d][c] = f;
        }
        
        //거쳐가는 정점
        for(int k = 1;k<=n;k++){
            for(int i = 1;i<=n;i++){
                for(int j=1;j<=n;j++){
                	//플로이드 와샬의 핵심
                    //기존의 가중치보다 k정점을 거친 가중치가 작다면 갱신
                    if(map[i][j]>map[i][k]+map[k][j]){
                        map[i][j] = map[i][k]+map[k][j];
                    }
                }
            }
        }
        
        int answer = Integer.MAX_VALUE;
        //시작점 S부터 K정점을 거쳐 A와 B까지 가는 최소거리 비교
        for(int k=1;k<=n;k++){
            answer = Math.min(answer, map[s][k]+map[k][a]+map[k][b]);
        }
        return answer;
    }
}

---

Result