기둥과 보 설치 : https://programmers.co.kr/learn/courses/30/lessons/60061
Problem



Solve
기둥과 보를 삭제할때 너무 어렵게 생각해서 어렵게 느껴졌던 문제. 삭제 방법만 알고나니 구현은 어렵지 않았다.
구조물이 만들어지는 배열을 [y][x][구조물]인 3차원 Boolean 배열로 구현해서 map[y][x][0]은 기둥 구조물 저장, map[y][x][1]은 보 구조물 저장을 따로따로 하도록 했다.
기둥과 보를 설치할때 문제에서 주어진 조건에 만족하면 map에 저장하고 만족하지 못하면 무시.
특히 구조물 설치 조건 만족여부를 판단하는 함수를 따로 분리했는데, 삭제할때도 사용하기 때문이다.
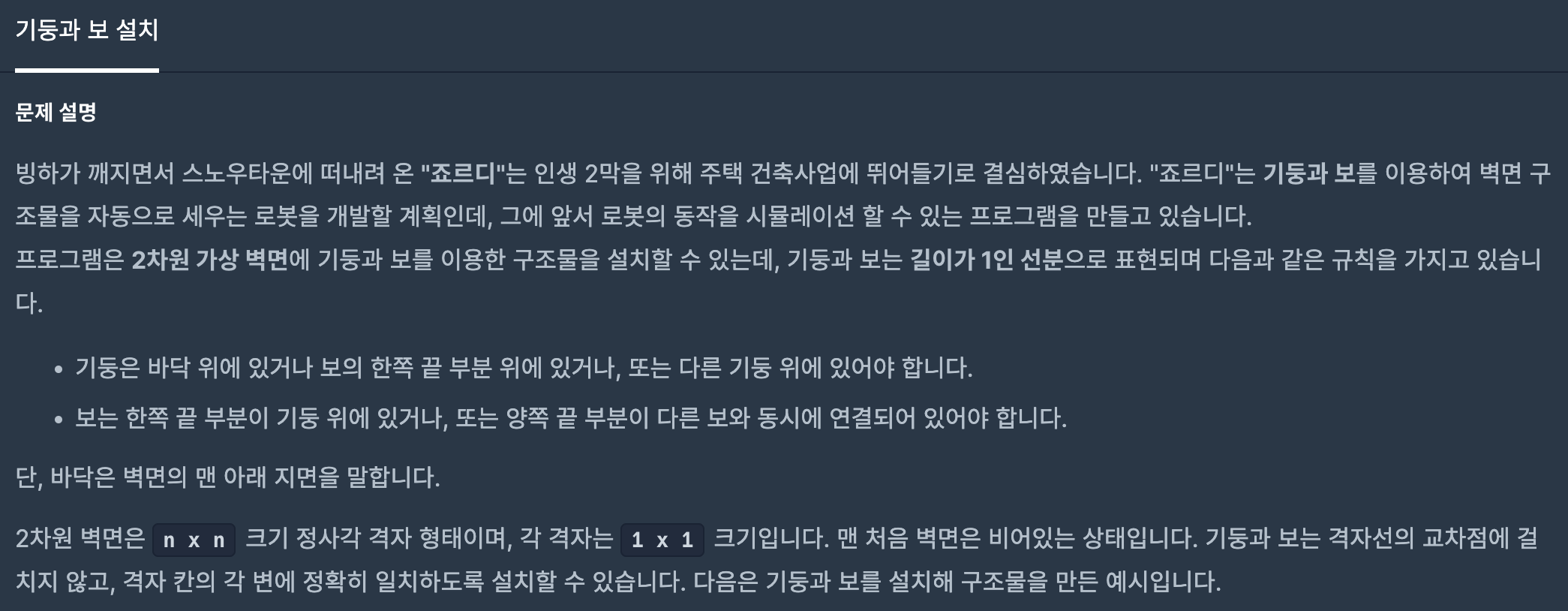
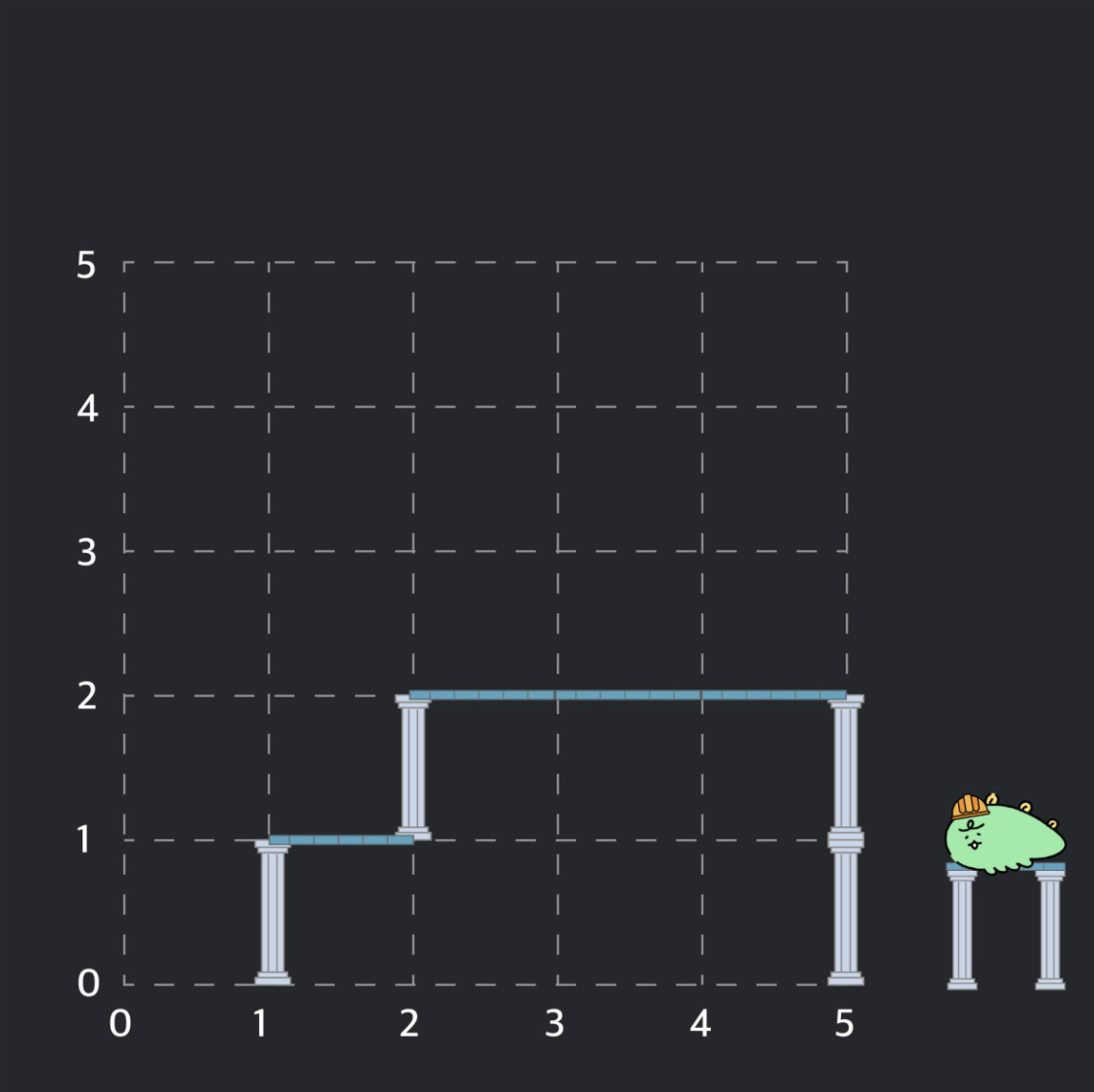
기둥 설치 조건은 기둥은 바닥 위에 있거나 보의 한쪽 끝 부분 위에 있거나, 또는 다른 기동 위에 있어야한다.
보 설치 조건은 보는 한쪽 끝 부분이 기둥 위에 있거나, 또는 양쪽 끝 부분이 다른 보와 동시에 연결되어 있어야 한다.
코드로 보면 아래의 checkPolliar와 checkBoard가 된다.
boolean checkPolliar(int x,int y){
//기둥이 바닥에 있는경우
if(y==0) return true;
//기둥의 왼쪽좌표에 보가있는경우(보는 (x-1,y)에 설치가 된다면 (x,y)까지 설치된것으로 판단)
//또는 현재 좌표에 보가 있는경우
else if(x-1>=0 && map[y][x-1][1] || map[y][x][1]) return true;
//기둥의 아래좌표에 기둥이있는경우(기둥은 (x,y-1)에 설치되면 (x,y)까지 설치된것으로 판단)
else if(y-1>=0 && map[y-1][x][0]) return true;
return false;
}
boolean checkBoard(int x,int y){
//보의 기준좌표(왼쪽)의 아래에 기둥이 존재하거나 오른쪽에 기둥이 존재하는 경우
if(map[y-1][x][0] || map[y-1][x+1][0]) return true;
//보의 기준좌표의 왼쪽에 보가 있고 오른쪽에도 보가 있는 경우
else if((x-1>=0 && map[y][x-1][1]) && map[y][x+1][1]) return true;
return false;
}삭제할때는 먼저 구조물을 삭제한다. 그런다음 map전체를 돌아다니면서 좌표에 기둥이 존재하면 기둥이 생성될수있는 조건인지, 보면 보가 생성될수 있는 조건인지 위에서 만든 만족여부를 판단하는 함수를 사용한다.
해당 조건을 만족하지 못한다면 구조물을 다시 복구 시킨다.
build_frame의 의 반복이 최대 O(1000), 반복 내부에서 생성은 O(1), 삭제는 최대 (100*100)이므로 해당 과정이 가지는 최악은 O(1000*10000)이므로 시간초과는 발생하지 않기 때문에 map을 전체 탐색하여 삭제 가능여부를 판단할수 있다.
구조물 상태는 위의 과정을 수행할때 생성될때 count++, 삭제될때 count--을 통해 구조물의 총 갯수를 구하여 answer[count][3]을 초기화한다.
그리고 x좌표 기준 오름차순, x가 같을땐 y기준 오름차순, x와 y둘가 같을땐 구조물 기준 오름차순으로 정렬해주어 배열을 반환해준다.
Code
import java.util.*;
class Solution {
boolean[][][] map;
int count;
int N;
public int[][] solution(int n, int[][] build_frame) {
map = new boolean[n+1][n+1][2];
count=0;
N = n;
//구조물 생성 or 삭제
for(int[] frame : build_frame){
build(frame);
}
int[][] answer = new int[count][3];
//map을 돌면서 true인 좌표, 구조물 저장
int idx = 0;
for(int i=0;i<=N;i++){
for(int j=0;j<=N;j++){
if(map[i][j][0]){
answer[idx][0]=j;
answer[idx][1]=i;
answer[idx++][2]=0;
}
if(map[i][j][1]){
answer[idx][0]=j;
answer[idx][1]=i;
answer[idx++][2]=1;
}
}
}
//x좌표기준 정렬, x가 같다면 y기준 정렬, 둘다 같다면 기둥기준 정렬
Arrays.sort(answer, new Comparator<int[]>(){
@Override
public int compare(int[] o1, int[] o2){
if(o1[0]>o2[0]) return 1;
else if(o1[0]==o2[0]){
if(o1[1]>o2[1]) return 1;
else if(o1[1]==o2[1]){
return o1[2]-o2[2];
}else return -1;
}else return -1;
}
});
return answer;
}
void build(int[] frame){
int x = frame[0];//x좌표
int y = frame[1];//y좌표
int a = frame[2];//0 : 기둥, 1 : 보
int b = frame[3];//0 : 삭제, 1 : 설치
if(b == 1){
if(a == 0){
//기둥 설치 조건 만족시 기둥설치
if(checkPolliar(x,y)){
map[y][x][0]=true;
count++;
}
}else{
//보 설치 조건 만족시 보 설치
if(checkBoard(x,y)){
map[y][x][1]=true;
count++;
}
}
}else{
if(a == 0){
//기둥 삭제
map[y][x][0] = false;
//map[][][0]과 map[][][1]을 돌면서 모든 구조물이 조건을 만족하지 않는다면 기둥 복구
if(!canDelete(y,x)) map[y][x][0] = true;
else count--;
}else{
//보 삭제
map[y][x][1] = false;
//map[][][0]과 map[][][1]을 돌면서 모든 구조물이 조건을 만족하지 않는다면 보 복구
if(!canDelete(y,x)) map[y][x][1] = true;
else count--;
}
}
}
//삭제 가능여부 판단
boolean canDelete(int y, int x){
//map 전체 탐색
for(int i=0;i<=N;i++){
for(int j=0;j<=N;j++){
//기둥이 있는 좌표에 기둥이 설치할 수 있는 조건인지 판단
if(map[i][j][0]){
if(!checkPolliar(j,i)) return false;;
}
//보가 있는 좌표에 좌표를 설치할 수 있는 조건인지 판단
if(map[i][j][1]){
if(!checkBoard(j,i)) return false;;
}
}
}
return true;
}
//기둥 설치 가능한 조건 판단
boolean checkPolliar(int x,int y){
if(y==0) return true;
else if(x-1>=0 && map[y][x-1][1] || map[y][x][1]) return true;
else if(y-1>=0 && map[y-1][x][0]) return true;
return false;
}
//보 설치 가능한 조건 판단
boolean checkBoard(int x,int y){
if(map[y-1][x][0] || map[y-1][x+1][0]) return true;
else if((x-1>=0 && map[y][x-1][1]) && map[y][x+1][1]) return true;
return false;
}
}