ShortGPT: Layers in Large Language Models are More Redundant Than You Expect

1. Background

최근 연구 동향

• LLM은 계속해서 모델 크기 확장으로 발전하고 있음
• 이에 비용 문제 해결을 위한 다양한 Compression 연구가 진행되고 있음.

Compression 방법과 한계

Quantization

• 모델 저장, 추론 비용 대폭 감소
• 모델 가중치를 부동소수점 -> 정수로 변환
• 특정 하드웨어 의존, 정확도 회복을 위해 추가 학습 하는 경우도 있음.

Pruning

• 모델의 중복된 부분 제거
• Unstructed Pruning : 모델이 Sparse 해짐
• Sturcted Pruning : 모델의 패턴을 지키며 가지치기
• 최근 연구는 복잡한 알고리즘들을 이용해서 가지치기함

Knowledge Distillation

• 부모 모델의 지식을 자식 모델에 주입하며 학습
• 하지만 Pruning에 비해 높은 Computing power 요구

Low Rank Factorization

• 가중치 행렬을 저순위 행렬로 근사하여 모델을 압축
• 마찬가지로 복잡한 알고리즘을 이용

간단한 Layer Pruning 방법 제안

1. Layer 중요도(BI) 확인
2. 중요하지 않은 Layer들에 Pruning 수행

2. Method

• Layer 중복성을 확인한 후, Layer 중요도를 평가하여 중요도가 낮은 Layer들에 대해 Pruning 수행

Layer Redundancy

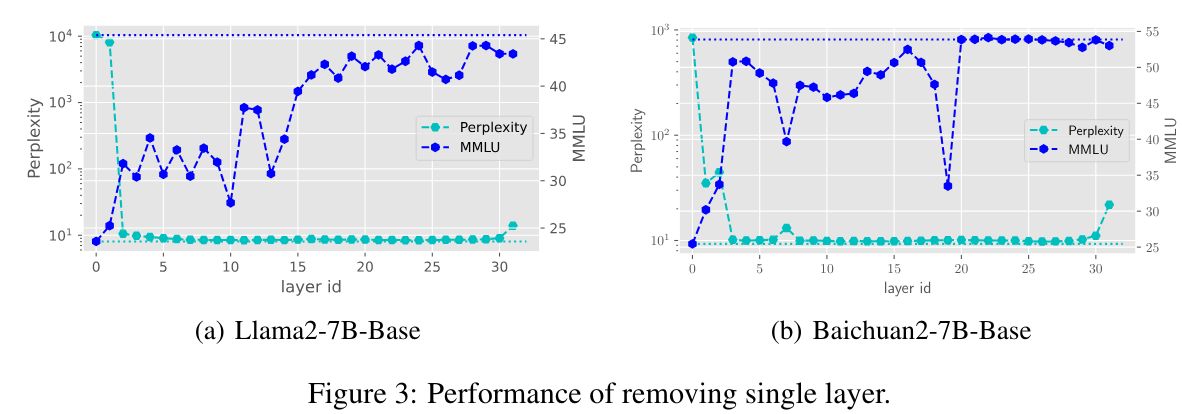
• Layer를 1개씩 제거하였을 때, 성능이 유지되는 부분이 존재함
• 주로 중후반부 Layer들을 제거하였을 때 성능변화가 작았음
• 중후반부 Layer들에 대해 Reduncancy가 존재한다는 것을 의미

Layer Importance

• Layer의 중복성을 학인하였으므로, 중복된 Layer를 Pruning할 예정.
• 중복된 Layer를 Pruning하기 위해 Layer 중요도 Metirc을 Block Influence (BI) 로 설정함.
  
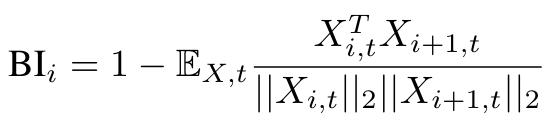
• BI는 각 layer가 모델의 hidden state에 얼마나 영향을 미치는지를 정량화하는 지표임.

수식 해석 및 중요도 계산 과정

1. Collect Hidden State:

• X_i,t 는 t시점에 i번째 layer의 hidden state를 의미
• 모델이 주어진 입력 데이터셋을 통해 추론할 때 각 layer의 hidden state X_i,t를 수집.

2. Calculate Cosine Similarity:

• i번째 layer와 다음 layer(i+1) 의 hidden state X_i,t와 X_i+1,t 사이의 cosine similarity 계산
• cos sim = 두 벡터 내적 / 두 벡터 크기의 곱

3. Block Influence:

• 해당 과정을 모든 t에 대해서 수행하여 cos sim을 계산하고, 이들을 평균냄.
• BI는 1-cos sim을 t시점에 평균 낸값으로 정의함
• 이는 각 layer가 hidden state를 얼마나 변화시키는지를 나타내며, 값이 클수록 해당 layer가 큰 변화를 일으킨다는 것을 의미.
• e.g) 인접한 두 layer가 연관이 높다? => cos sim이 1에 가까워짐 => BI 작음 => layer가 연관이 높으므로 제거 대상

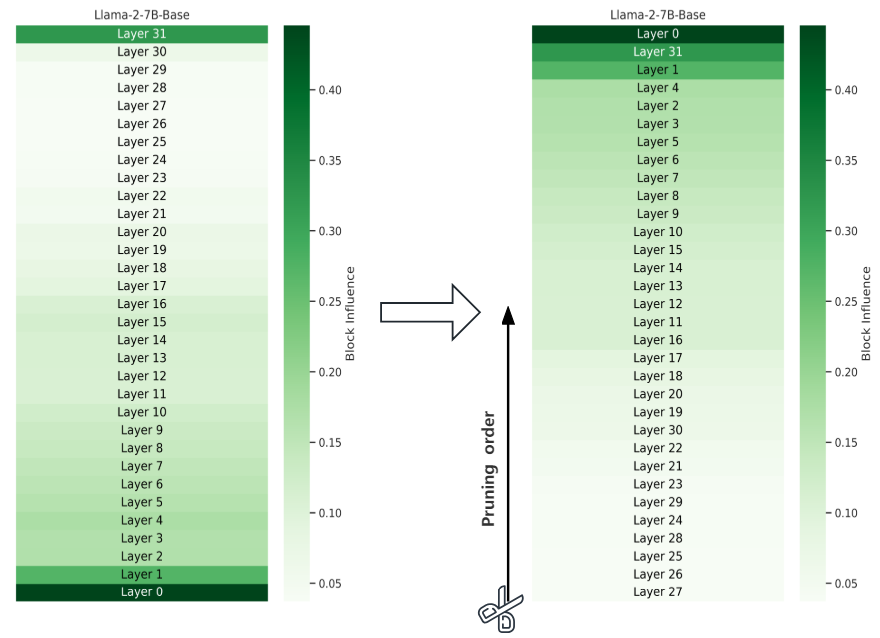
Layer Removal

• BI를 오름차순으로(작은 순) 정렬하고, BI가 낮은 Layer를 Pruning
• 해당 method를 ShortGPT라고 정의
  

3. Experimental Setup

Model

• 영어 - LLaMA2 7B, 13B
• 중국어 - Baichuan2 7B, 13B

Benchmark

MMLU

• 모델의 n-shot learning을 통해 학습된 모델을 측정하기 위한 벤치마크.
• 57개의 하위 task를 포함하며, task 난이도는 초급부터 고급 전문 수준까지 다양함.

CMMLU

• CMMLU는 중국어 추론 능력을 평가하기 위해 설계된 포괄적인 중국어 평가 데이터셋.
• 67개의 하위 task를 포함하며, task 난이도는 초등학교부터 전문가 수준까지 다양함.

Baseline

• ShortGPT는 Structed Pruning임.
• Structed Pruning Method로 LLMPrun, SliceGPT, LaCo 로 비교 수행
• ShortGPT/LaCo 는 Layer Pruning => Depth Pruning
• LLMPrun/SliceGPT는 Dimension Pruning => Width Pruning

4. Result

• 일반적으로 Structed Pruning은 파라미터를 30% 이하로 줄임.
• 해당 결과는 대략 25% Pruning Ratio로 실험 수행
  
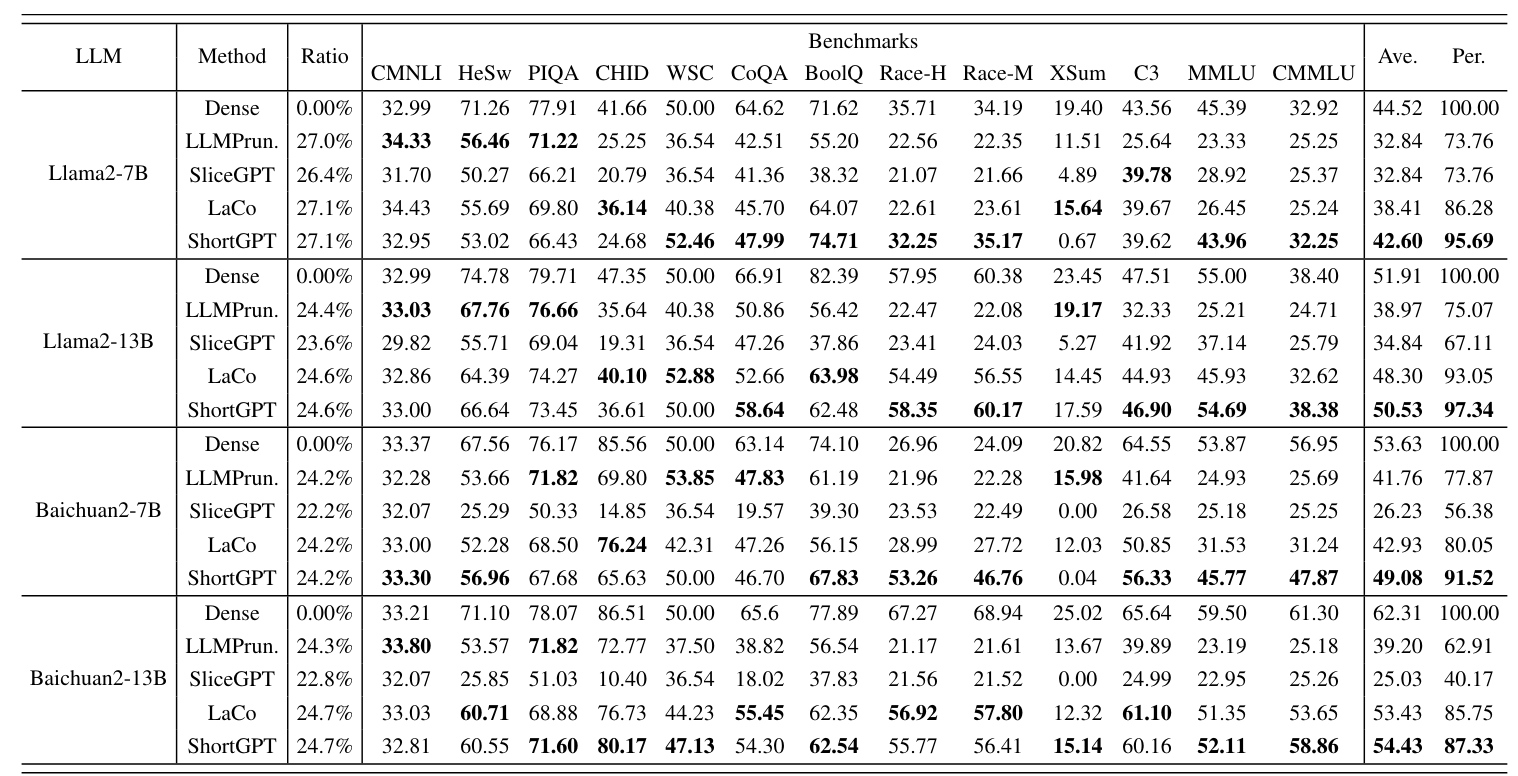
• Baseline method들과 비교하였을때 sota 달성
• benchmark에서 원본 성능을 최대한 유지하였음
• ShortGPT에서 사용한 Depth Pruning 방법이 Width Prunig 방법보다 좋은 성능을 보여줌
• 즉, 너비보다 폭에서 더 많은 중복성을 가지고 있다는 의미.

5. Analysis

Depth Redundancy vs Width Redundancy

• 깊이 기준 중복성과 너비 기준 중복성 비교
• 깊이는 Layer를 기준으로, 너비는 attention head를 기준으로 사용

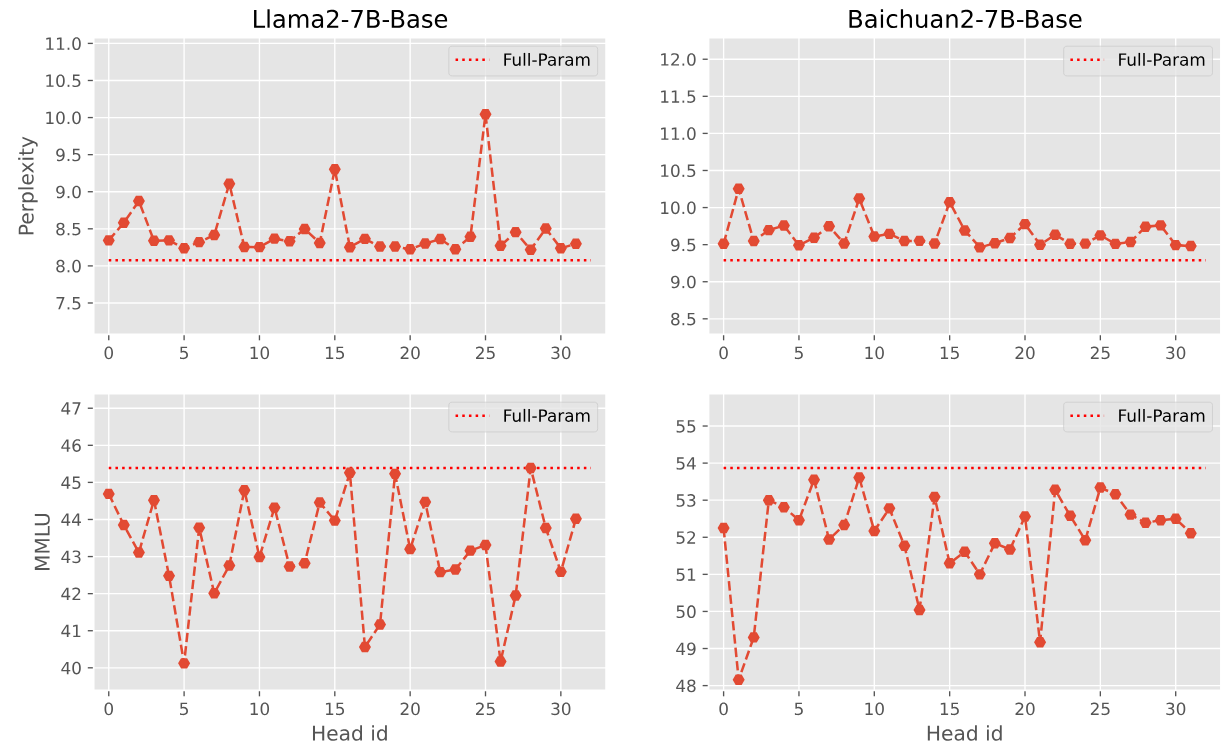
• 위에서 조사했던 Layer(Depth) Redundancy에서는 각자 다른 모델에서 특정 부분에서 Redundacny가 존재하는 것을 발견하였음.
• 동일한 방법으로 Attention Head(Width) Redundancy 조사 결과, Depth Redundancy에서의 패턴이 보이지 않음.
• 즉, Width Rudundancy보다 Depth Rudundacny가 크다는 것을 의미함.

Layer Importance Metirc

• Layer Importance를 측정하는 지표로 4가지 방법을 실험
• Sequential : 얕은 layer부터 중요하다고 가정하는 경우
• Reverse-order : sequential 의 역순으로, 깊은 layer부터 중요하다고 가정하는 경우
• Relative Magnitude : layer가 input에 변화를 주는 정도로 layer의 중요성 판단. 변화량이 클수록 중요도가 크다는 가정.
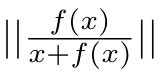
  x는 input, f는 layer 통과를 의미
  e.g) layer를 통과했을 때 어떤 layer는 1, 어떤 layer는 3배만큼 변화시킨다고 가정
  input으로 3이 들어온다면, 1배만큼 변화시키는 layer의 중요도는 1/2.
  input으로 3이 들어온다면, 3배만큼 변화시키는 layer의 중요도는 3/4.
  결과적으로 layer를 통과했을 때 변화량이 클수록 중요도가 높다는 가정
• BI : 위에서 설명하였음

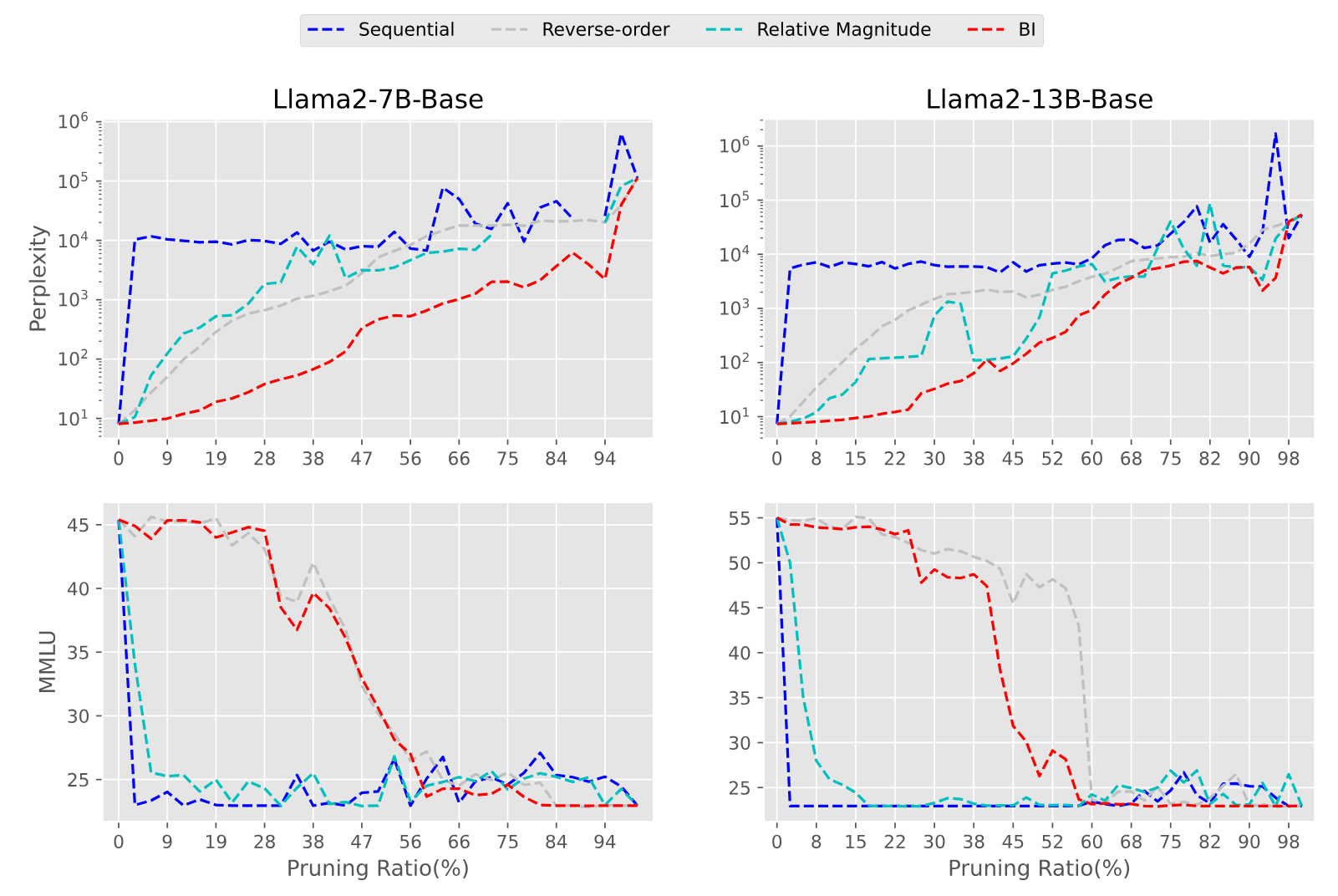
• Perplexity(PPL) 가 BI로 측정하였을 때 가장 낮게 나옴
• MMLU 지표는 BI로 측정하였을 때 가장 높게 나옴
• 즉, 다른 지표를 사용하였을 때보다 BI를 중요도 지표로 채택할 때 가장 좋은 성능을 끌어냄

Quantization 과 함께 사용

• Quantized Model에 ShortGPT 방법 적용
  
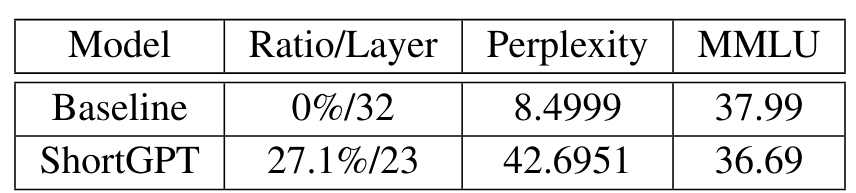
• MMLU 지표가 거의 유사한 수준임.
• Quantization과의 연계가 가능함.

Conclusion

Summary

• Layer Redundacny 발견
• BI 라는 새로운 Layer Importance Metric 정의하여 Layer Pruning 수행
• Structed Prunig 에서 sota를 달성.
• Quantization과 연계하여 추가적인 비용 감소가 가능.

Limitation

• Post Training에 대한 결과는 없으며 현재 연구 중이라고 함.