[Paper Review] GPTQ: ACCURATE POST-TRAINING QUANTIZATION FOR GENERATIVE PRE-TRAINED TRANSFORMERS
Paper Review
목록 보기
9/20
GPTQ: ACCURATE POST-TRAINING QUANTIZATION FOR GENERATIVE PRE-TRAINED TRANSFORMERS
1. Background
최근 연구 동향
- LLM은 뛰어난 언어 모델링 능력을 갖추고 있지만 추론 시 과도한 비용이 들어감
- e.g) GPT3-175B 는 16bit일때 326GB 메모리가 필요함
- 비용 문제 해결하기 위해 Compression 기법 중 Quantization 연구가 활발히 진행중
Quantization 연구의 한계
- 크게 학습 중 양자화(QAT), 학습 후 양자화(PTQ) 로 나누어짐.
- 수십억 개의 파라미터를 갖는 모델을 양자화하면서 학습(QAT)하기에는 너무 비쌈.
- 3,4bit 로의 PTQ 양자화는 양자화 오류를 해결하는 것이 복잡해져 매우 어려움.
- 모델 규모가 커질수록 PTQ에서 복잡한 양자화 기법이 필요하고, 이는 연산량과 메모리 사용량이 증가한다는 의미
GPTQ 제안
- PTQ 방법론
- 3, 4 비트로 양자화하여도 손실 거의 없음 (low bit Quantization 성능)
- 2 비트에서도 안정적인 성능을 보임 (lower bit Quantization 성능)
- 수백억개의 초대규모 모델도 4시간 내에 PPL 증가 없이 양자화 가능 (학습 효율성)
2. Based Algorithms
Layer-Wise Quantization
- 각 layer 별로 독립적으로 양자화 수행 -> layer 기준으로 양자화
- 하단의 목적함수를 가지고 양자화를 수행
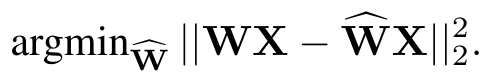
- input으로 X가 들어갈 때, 원본 결과 WX와 양자화된 결과 W^X 의 차이가 작아지게끔 양자화 수행
Optimal Brain Quantization (OBQ)
- 양자화 중 발생하는 오차를 보상하기 위해 상단의 목적함수를 이용하여 잔여 Weight를 조정하는 방법
- Weight 값 1개씩 Sequential 하게 이루어지는 Quantization -> Greedy Algorithm
- 다음의 순서대로 OBQ 진행됨
- Hessian Matrix 계산
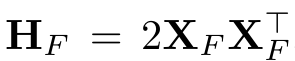
- 목적함수를 2차 미분한 결과 행렬
- Hessian Matrix의 의미는 input에 대해 목적함수의 기울기가 어떻게 변하는가를 나타낸 것.
- Hessian Matrix의 성질은 이계도함수가 연속일 때, Symmetric Matrix 임.
- H는 헤세 행렬, X는 input, F는 아직 양자화하지 않은 Weight
- 양자화 수행할 Weight 선택
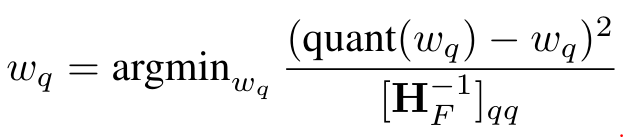
- 아직 양자화하지 않은 행렬(F) 에서 양자화를 수행할 값(wq) 선택하는 과정
- F의 전체 값들을 하나씩 해당 공식에 적용하면서 가장 작은 값을 양자화 수행할 Weight로 최종 선택
- quant(wq) 는 wq를 RTN으로 calibrate(=quantize) 수행한 값
- (quant(wq) - wq)^2 의 argmin을 구함으로써 양자화 오차를 최소화함
- [H^-1F]qq 는 헤세 행렬의 q인덱스에서의 대각성분을 의미이며, q번째 weight가 목적 함수에 미치는 영향을 의미하게 되고, 이는 곧 weight의 중요성을 의미하게 됨.
- 양자화 수행 및 양자화 수행 안한 Weight들은 Update
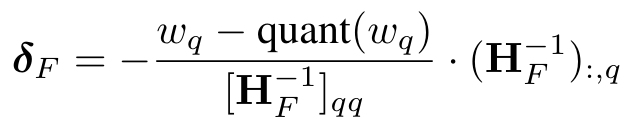
- 선택된 가중치 (wq) 를 양자화 진행
- 나머지 weight들 (F) 는 해당 공식에 의해 Update됨.
- δf : 남은 가중치 F 를 Update한 값
- H^-1q : 헤세행렬의 역행렬에서 q번째 열 값
- 헤세 행렬 Update
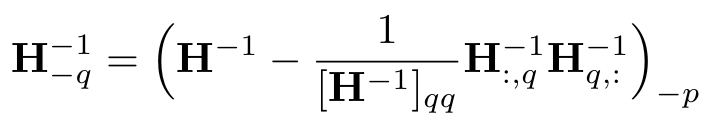
- 헤세 행렬의 역행렬을 update하여 다음 가중치 양자화 스텝에 대비함.
- q번째 index의 값을 양자화하였을때, 해당 값을 제거하여 update
- 반복하여 모든 가중치에 적용
- 1~4 과정을 반복하여 모든 weight 값들을 Quantize 수행
Summary
- 오차가 가장 작은 가중치를 선택
- 선택된 가중치를 양자화
- 양자화로 인한 오차를 계산하고, 남은 가중치를 Update하여 오차를 보상
- 모든 가중치가 양자화될 때까지 과정 반복
3. Method
- GPTQ 알고리즘은 Layer-Wise Quantization 도중 OBQ를 base로 한 GPTQ 과정을 따름.
Suggested Algorithm: GPTQ
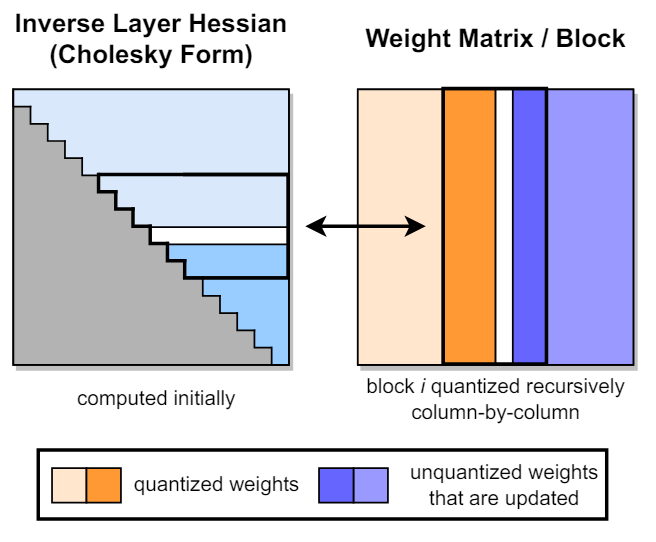
- 초기 Inverse Hessian Matrix를 Cholesky Decomposition 하여 상삼각행렬 획득
- Weight 내부에서 일부 Block을 지정하고, Block 내부의 열을 계산하며 Block 내부의 나머지 Weight를 Update를 수행함.
- Block 내 모든 columns에 대해 양자화가 완료되면, 전체 잔여 Weight를 Update하고, 전체 잔여 Inverse Hessian Matrix 도 Update 수행.
1. Row-Wise Quantization
- OBQ에서의 오차가 작은 순서가 아닌 랜덤 순서로 양자화해도 LLM 양자화 성능은 비슷하므로, OBQ 방법처럼 greedy하게 update하는 방법은 비효율적임.
- OBQ는 1개 update 시마다 잔여 weight와 Hessian Matrix를 모두 Update 수행하는데, weight의 모든 행에서 내부값들을 동일한 순서로 양자화하면, H^-1F는 항상 동일하게 유지되어 OBQ에서처럼 Hessian Matrix를 Update할 필요가 없음.
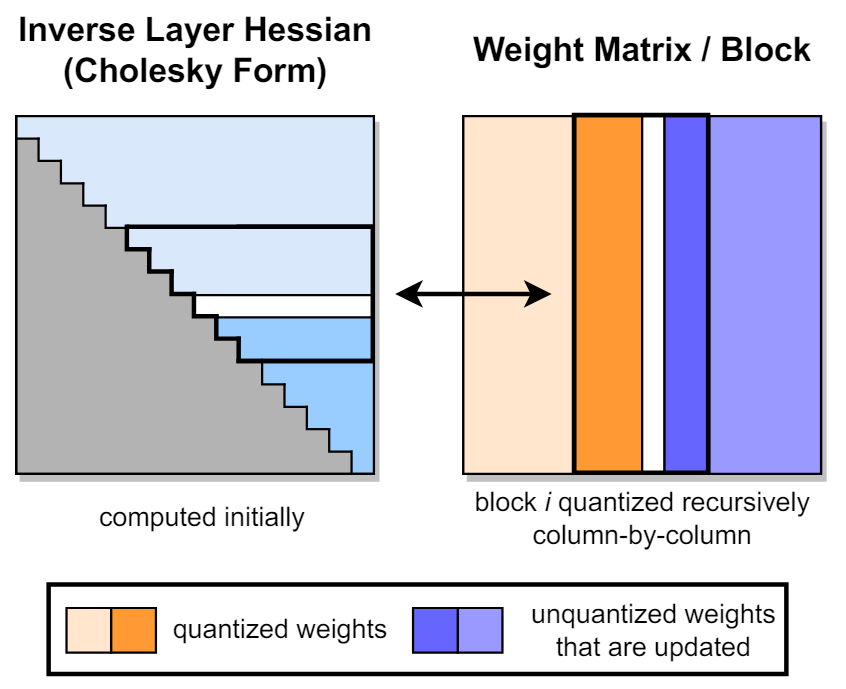
- Inverse Hessian 의 row 와 Weight의 Column 이 같은 영역을 차지함. 따라서 Hessian을 업데이트할 필요가 없음
- Weight 양자화를 모든 row에 대해 동일한 순서대로 column 단위로 양자화하는 방법을 제안
2. Block-Wise Update
- OBQ 방식은 Weight의 모든 요소를 Update 하기 위해 메모리에 접근을 자주해야함.
- 열을 한 번에 B개씩 처리하는 Block을 생성하고, 각 Block이 완전히 양자화된 후 전체 잔여 Weight와 H^-1의 해당 Block을 update 하는 방법 제안
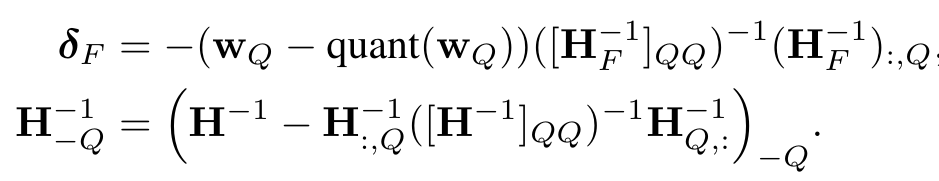
- 잔여 Weight 수정 방법과 H^-1 을 update하는 과정은 위에서 설명하였던 OBQ 방법과 동일하되, update과정에서 Block 단위를 고려한 결과.
3. Cholesky Reformulation
- Block 단위로 update를 수행하는 경우, lazy 한 update 과정이므로, Inverse Hessian Matrix가 Indefinite(부정부호) Matrix가 되어 가중치 업데이트가 잘못될 수 있음.
- Hessian Matrix = 2XXT 이므로, cholesky decomposition 이 가능하여, H를 Cholesky form 으로 변환이 가능함.
- Cholesky form은 삼각행렬이라서 Hessian Matrix를 그대로 사용하는 것보다 훨씬 안정적임
- Hessian Matrix를 Cholesky form 으로 변환하는 방법 제안
Summary
- Inverse Hessian Matrix를 Cholesky Form으로 변환
- 각 Block에서 Column-Wise 양자화 수행하며 Block 내 나머지 Weight Update
- Block 양자화가 끝나면 나머지 전체 Weight와 Inverse Hessian Matrix Update
- 1~3과정을 반복하여 모든 Weight 양자화
4. Result
Modality Expandation
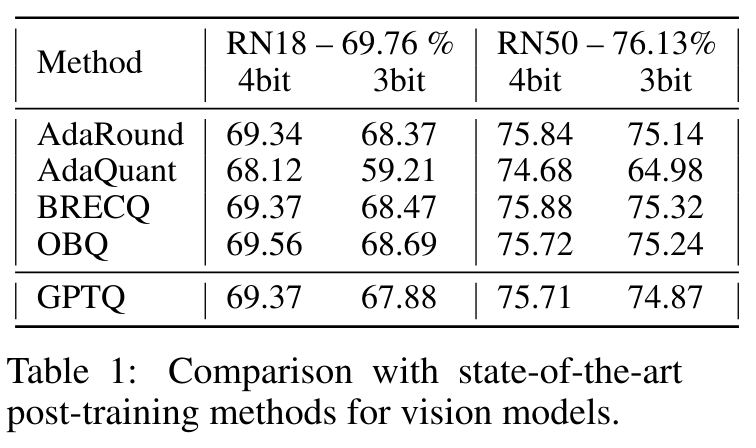
- 비전 모델(ResNet) 에서도 좋은 양자화 성능을 보임
Runtime

- 30B 모델은 몇 분만에, 초대형 175B 모델은 몇 시간만에 양자화 가능
Perplexity 로 성능평가
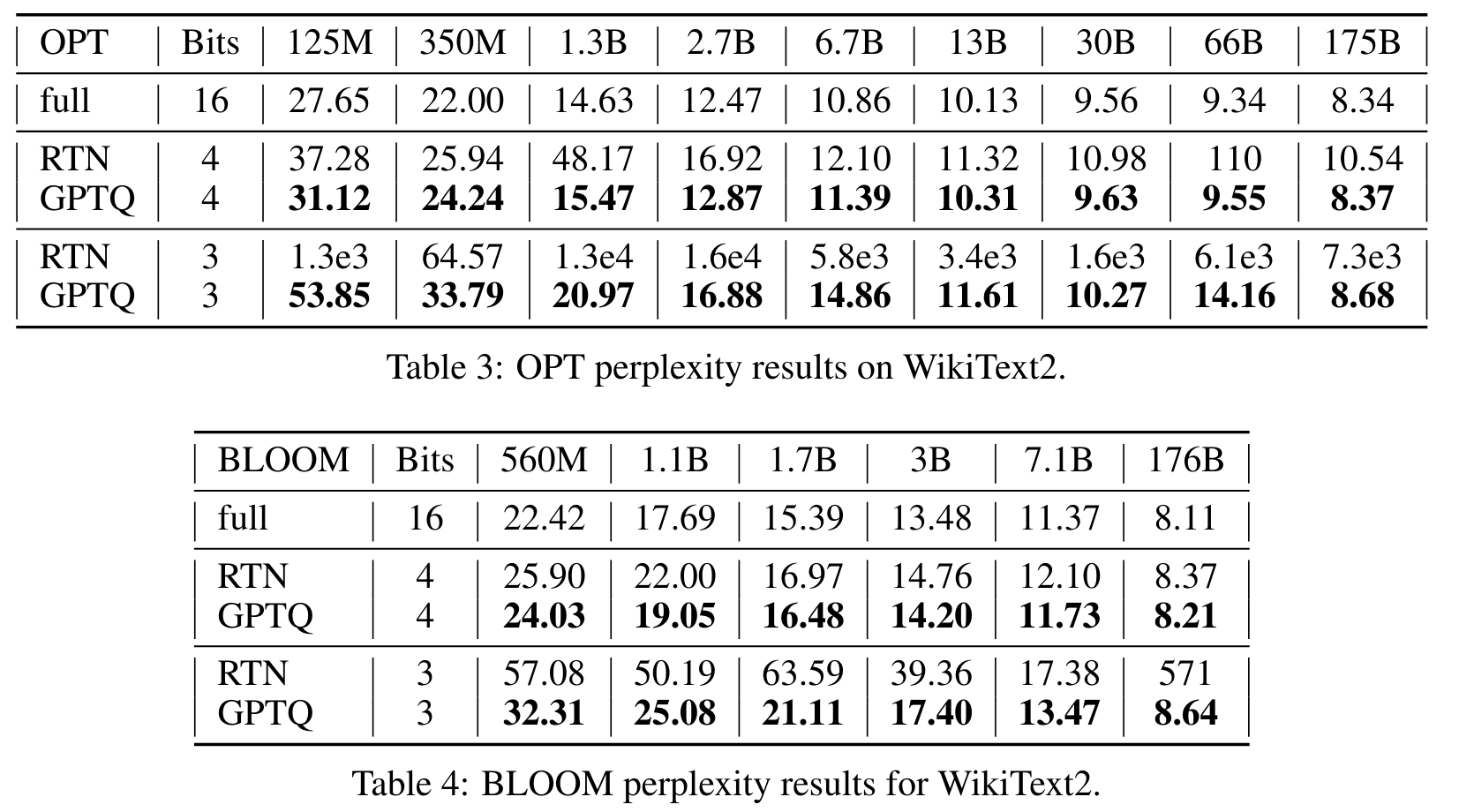
- 모델 규모가 커질수록 안정적으로 양자화가 잘됨
- 3bit에서는 RTN은 붕괴되지만, GPTQ는 성능을 유지함
Zero-Shot
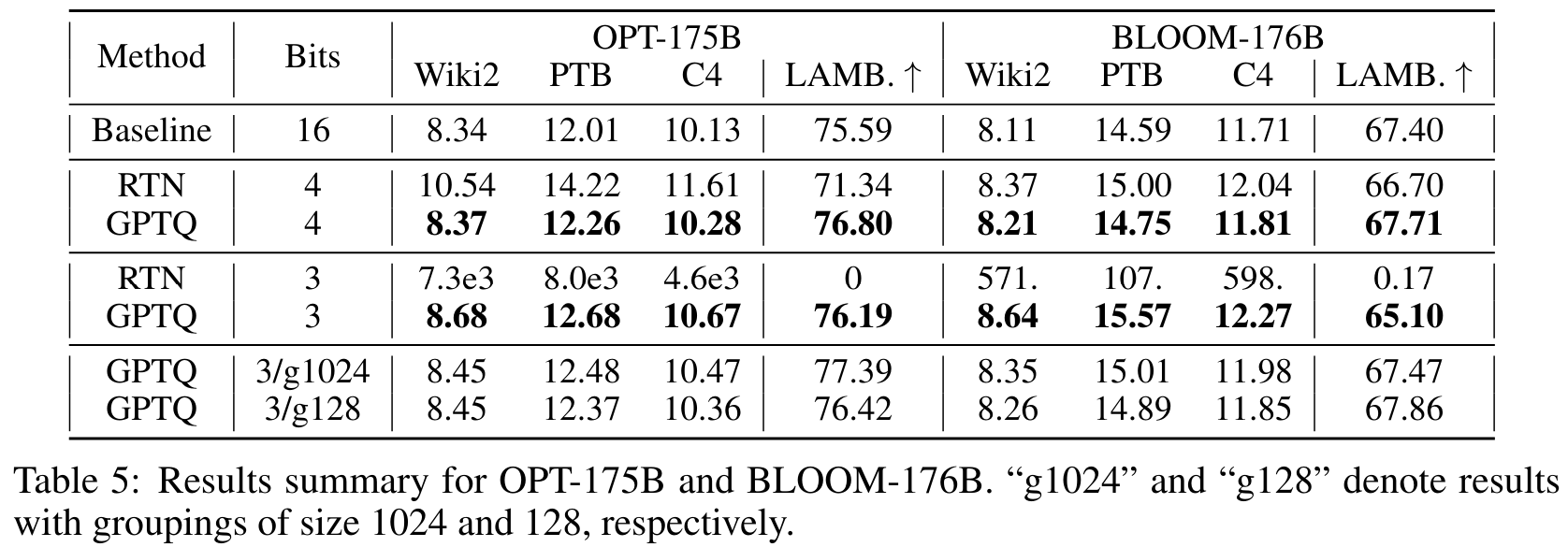
- 여러 zero shot task에서도 평균적으로 좋은 성능 보여줌
5. Conclusion
Summary
- 다양한 zero-shot task에서 좋은 성능 기록
- 극단적인 양자화 설정에서도 모델의 성능을 유지하여, 높은 압축 비율과 효율성을 동시에 달성할 수 있음.
Limitation
- Weight만 양자화하고, Activation은 양자화하지 않았음.

