[백준] 10844 쉬운 계단 수

문제

45656이란 수를 보자.

이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.

N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

입력

첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

출력

첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.

예제 입력

1

예제 출력

9

풀이

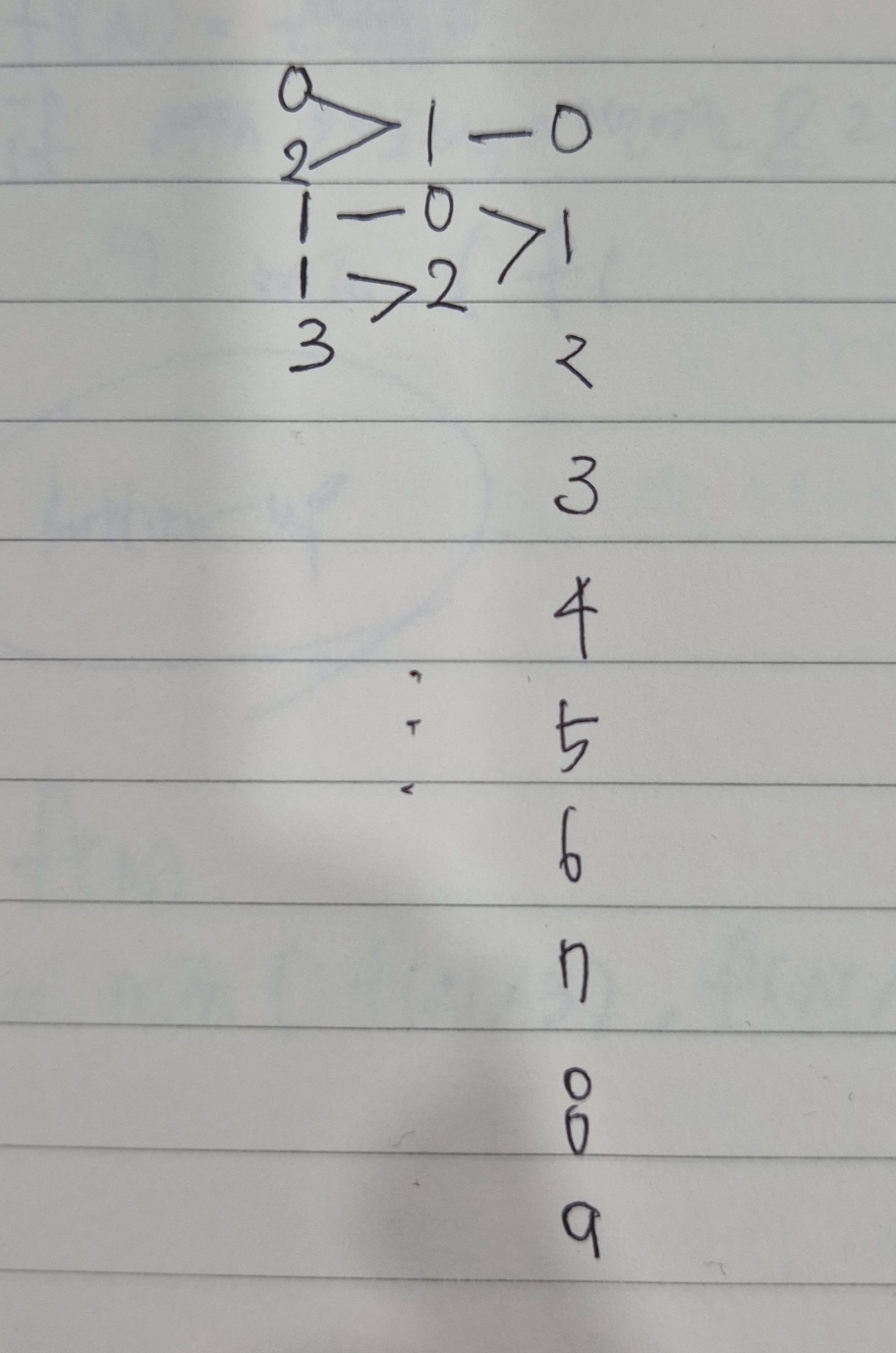풀이는 위와 같다. 1번째를 제외한 k번째 자릿수에 오는 경우는 0~9이다. 그러면 해당 숫자는 k-1번째 계단의 해당 숫자와 연결될 수 있는 숫자가 있을때 올 수 있는 경우의 수들의 합이다. 이걸 반복해서 앞으로 가면 결국 1번째 계단의 숫자들이 가질 수 있는 경우의 수들을 이용하게 된다.

따라서 우리는 1번째 계단의 각각의 숫자들이 가지는 경우의 수들의 합을 알면 되는데, 1번째가 시작이므로 모두 1을 가진다.

m번째 계단의 숫자 n이 가질 수 있는 계단 수를 점화식으로 나타내면 다음과 같다.

f(m,n) (m > 0)
1) m = 1 일때
f(m,n) = 1
2) m != 1 이고 n = 0 일때
f(m,n) = f(m,n) + f(m-1,1)
2) m != 1 이고 n = 9 일때
f(m,n) = f(m,n) + f(m-1,8)
3) m != 1 이고 n != 0 이고 n != 9 일때
f(m,n) = f(m,n) + f(m-1, n-1) + f(m-1,n+1)

주의 사항
1번째 계단에 0이 올 수 없으므로 dp[1][0] = 0으로 설정한다.

n = int(input())
dp = [[0 for _ in range(10)] for _ in range(n+1)] # 0번째 배열은 무시
for i in range(10): # 1번째 자리의 숫자가 해당 자리에 오기까지 가지는 경우의 수
    if i == 0: dp[1][i] = 0
    else: dp[1][i] = 1

for i in range(2,n+1):
    for j in range(10):
        if j == 0: dp[i][j] = dp[i][j] + dp[i-1][1]
        elif j == 9: dp[i][j] = dp[i][j] + dp[i-1][8] 
        else: dp[i][j] = dp[i][j] + dp[i-1][j-1] + dp[i-1][j+1]
print(sum(dp[n]) % 10**9)