[백준] (실패)

문제

안양에 사는 상혁이는 4년간의 통학에 지쳐 서울에 집을 구하려고 한다. 상혁이가 원하는 집은 세가지 조건이 있다.

맥세권 : 맥세권인 집은 맥도날드와 집 사이의 최단거리가 x이하인 집이다.
스세권 : 스세권인 집은 스타벅스와 집 사이의 최단거리가 y이하인 집이다.
맥세권과 스세권을 만족하는 집 중 최단거리의 합이 최소인 집
통학 때문에 스트레스를 많이 받은 상혁이는 집을 선택하는 데 어려움을 겪고 있다. 똑똑한 여러분이 상혁이 대신 이 문제를 해결해 주자. 이사 갈 지역의 지도가 그래프로 주어지고 맥도날드와 스타벅스의 위치가 정점 번호로 주어질 때 상혁이가 원하는 집의 최단거리의 합을 출력하는 프로그램을 작성하시오. (맥도날드와 스타벅스가 아닌 정점에는 모두 집이 있다.)

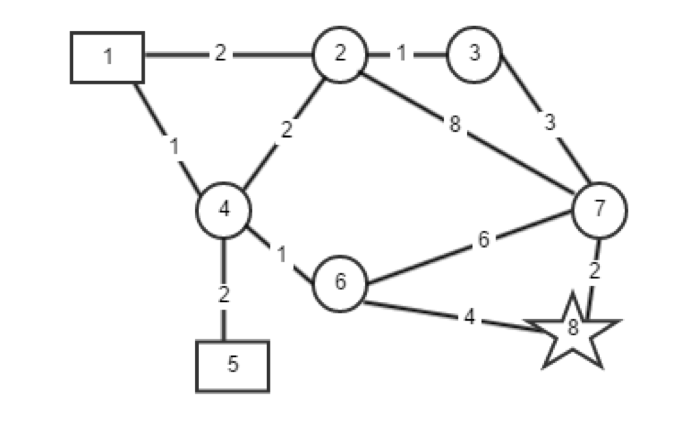
위의 예제 지도에서 사각형은 맥도날드를, 별은 스타벅스가 위치한 정점을 나타낸다. 각 원은 집이 있는 정점을 낸다. x가 6이고 y가 4일 때 가능한 집의 정점은 6이다. 맥도날드까지의 최단거리가 2, 스타벅스까지의 최단거리가 4로 총 합이 6이 되기 때문이다. 정점 7은 맥세권이면서 스세권이지만 맥도날드까지의 최단거리가 6, 스타벅스까지의 최단거리가 2로 총 합이 8로써 정점 6의 값보다 크므로 답이 아니다. 그 외의 정점 2, 3, 4는 맥세권이면서 스세권인 조건을 충족하지 못하므로 답이 될 수 없다.

입력

첫줄에는 정점의 개수 V(3 ≤ V ≤ 10,000)와 도로의 개수 E(0 ≤ E ≤ 300,000)가 주어진다. 그 다음 E줄에 걸쳐 각 도로를 나타내는 세 개의 정수 (u,v,w)가 순서대로 주어진다. 이는 u와 v(1 ≤ u,v ≤ V)사이에 가중치가 w(1 ≤ w < 10,000)인 도로가 존재한다는 뜻이다. u와 v는 서로 다르며 다른 두 정점 사이에는 여러 개의 간선이 존재할 수도 있음에 유의한다. E+2번째 줄에는 맥도날드의 수 M(1 ≤ M ≤ V-2) 맥세권일 조건 x(1 ≤ x ≤ 100,000,000)가 주어지고 그 다음 줄에 M개의 맥도날드 정점 번호가 주어진다. E+4번째 줄에는 스타벅스의 수 S(1 ≤ S ≤ V-2)와 스세권일 조건 y(1 ≤ y ≤ 100,000,000)가 주어지고 그 다음 줄에 S개의 스타벅스 정점 번호가 주어진다.

맥도날드나 스타벅스가 위치한 정점에는 집이 없다.
한 정점에 맥도날드와 스타벅스가 같이 위치할 수 있다.
집이 있는(= 맥도날드나 스타벅스가 위치하지 않은) 정점이 하나 이상 존재한다.

출력

상혁이가 원하는 집의 맥도날드까지의 최단거리와 스타벅스까지의 최단거리 합을 출력한다. 만일 원하는 집이 존재하지 않으면 -1을 출력한다.

예제 입력 1

8 11
1 2 2
1 4 1
2 4 2
2 3 1
2 7 8
3 7 3
4 5 2
4 6 1
6 7 6
6 8 4
7 8 2
2 6
1 5
1 4
8

예제 출력 1

6

풀이

맥도날드 지점들을 모두 우선순위큐에 다 넣고 다익스트라 수행, 스타벅스 지점들을 모두 우선순위 큐에 넣고 다익스트라 수행한다.
이후 맥세권 거리 + 스세권 거리의 합이 최소인 값을 구하면 된다.

(주의사항)
1.메모리 사용량 고려(그래프 정보 저장 시 인접 행렬 X, 인접 리스트 O)
정점 간 연결정보를 2차원 배열(=인접 행렬)로 저장하려 했는데, 그렇게 되면 (V+1) * (V+1) 크기의 배열이 된다. 문제에서 주어진 V의 최댓값이 10,000 이므로 1억칸, int 한 칸을 4바이트만 잡아도 400MB 이상이다. 따라서 정말 연결된 정점 정보들만 저장할 수 있는 인접 리스트를 사용해야 한다.

2.시간복잡도 차이
인접 행렬의 다익스트라를 돌리면 1억 번 연산이 발생한다. 간선이 적은 희소 그래프인 경우 불필요한 낭비가 심하다. 따라서 인접 리스트를 사용하여 갈 수 있는 간선만 순회토록 한다.

import sys
from queue import PriorityQueue
input = sys.stdin.readline

# 정점 개수 V, 도로 개수 E
V, E = map(int, input().split())
# 그래프 저장할 배열(-1 이면 연결안되어 있는걸로), 가중치 저장 위해 2차원!
g = [[] for _ in range(V+1)]
# 그래프 정보 입력 받음
for _ in range(E):
    u, v, w = map(int, input().split())
    # 양방향이므로 넣어줌
    g[u].append((v,w))
    g[v].append((u,w))
# 맥세권 정점 수, 조건, 정점 정보 입력 받음
M, x = map(int, input().split())
mArr = list(map(int, input().split()))
# 스세권 정점 수, 조건, 정점 정보 입력 받음
S, y = map(int, input().split())
sArr = list(map(int, input().split()))

# 풀이
# 다익스트라 돌리는데, 
# 맥세권 좌표 다 넣어서 한번에 다익 돌리고 
# 스세권 좌표 다 넣어서 한번에 다익 돌려서
# 각각의 dist 의 합이 조건 만족하면서 최소되는거 고르기
distM = [1e9 for _ in range(V+1)]
distS = [1e9 for _ in range(V+1)]

def dijkstra(type):
    # 우선순위 큐 생성
    pq = PriorityQueue()
    # 타입에 따라 관련 정점 정보 다 넣음
    if type == 'mac':
        for m in mArr:
            pq.put((0, m)) 
            distM[m] = 0 # 거리 갱신(현재는 등록)
    elif type == 'star':
        for s in sArr:
            pq.put((0, s))
            distS[s] = 0 # 거리 갱신(현재는 등록)

    # 다익돌리기
    while not pq.empty():
        w, n = pq.get()
        # mac 인 경우
        if type == 'mac' and distM[n] != w:
            continue
        # star 인 경우
        elif type == 'star' and distS[n] != w:
            continue
        # 인접 노드 갱신 nn 는 인접 정점 번호, w 는 거리, -1이 초기값
        for nn, ww in g[n]: 
            # idx 가 0 이 아니고 w 가 -1 이 아닌 경우에만
            if nn == 0 or ww == -1: continue
            # mac 인 경우 (star 거쳐가도 됌)
            if type == 'mac':
                caledDist = ww + w
                if distM[nn] <= caledDist: continue
                distM[nn] = caledDist
                pq.put((caledDist, nn))
            # star 인 경우 (mac 거쳐가도 됌)
            if type == 'star':
                caledDist = ww + w
                if distS[nn] <= caledDist: continue
                distS[nn] = caledDist
                pq.put((caledDist, nn))

dijkstra('mac')
dijkstra('star')

min_val = 1e9
for i in range(1, V+1):
    if i in mArr or i in sArr:
        continue
    if distM[i] <= x and distS[i] <= y:
        min_val = min(min_val, distM[i] + distS[i])

if min_val == 1e9:
    print(-1)
else:
    print(min_val)