문제

이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.

노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.

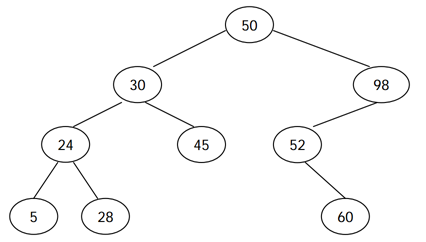
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.

이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.

입력

트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.

출력

입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.

예제 입력 1

50
30
24
5
28
45
98
52
60

예제 출력 1

5
28
24
45
30
60
52
98
50

풀이

트리 문제를 접한 적이 없어서 트리 관련 기초 문제를 2개 풀어본 후, 다시 들여다 보았다.

그래도 안풀려서 타 블로그의 풀이를 보니, 두 가지 방법으로 풀 수 있다는 것을 알았다.

1. Node 클래스를 생성하여 전위 순회 결과를 사용하여 직접 BST 트리를 구현
2. 전위 순회 방식에 대한 이해를 바탕으로 전위 순회 배열을 사용해 후위 순회 배열을 생성

풀이1 - Node 클래스를 생성하여 전위 순회 결과를 사용하여 직접 BST 트리를 구현

Node 클래스를 생성하여 전위 순회 결과를 사용하여 직접 BST 트리를 구현하는 방법
전위 순회 결과의 제일 첫 번째 원소가 해당 트리의 루트이기 때문에, 해당 값을 루트로 두고, 나머지 원소들로 완전 이진 트리를 만들어나가는 방법이다.

이를 위해 Node 클래스와 BST 를 만드는 함수를 구현하여 BST 를 그린 후에, 후위 순회 함수를 통하여 BST 를 순회하면 된다.

BUT, 이렇게 하면 사실상 전위 순회 배열을 효과적으로 사용하는게 아니라, 루트 값만을 사용하고 나머지 값들은 위치에 상관없이 그냥 집어넣어서 BST 를 만드는 것이기 때문에 문제가 의도한 바는 아니라고 생각한다.

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

arr = []
while True:
    try:
        arr.append(int(input().strip()))
    except:
        break
print(arr)

# 이진 탐색 트리 노드 정의
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

# BST 삽입 함수
def insert(root, val):
    if val < root.val:
        if root.left is None:
            root.left = Node(val)
        else:
            insert(root.left, val)
    elif val > root.val:
        if root.right is None:
            root.right = Node(val)
        else:
            insert(root.right, val)

# 후위 순위 L -> R -> ROOT
def post_order(node):
    if node is None:
        return 
    post_order(node.left)
    post_order(node.right)
    print(node.val)

root = Node(arr[0])
for v in arr[1:]:
    insert(root, v)

post_order(root)

그러나 위와 같이 구현하면 백준에서 시간 초과가 발생한다. 이를 해결하기 위해 트리를 생성하는 재귀 형태의 insert 함수를 반복문 형태의 insert 함수로 바꿔준다. 이 과정에서, 각 함수의 root 매개변수가 의미하는 바가 다르다.

재귀 형태의 insert 함수

• root: 현재 내가 위치한 노드 객체
• val: 삽입하고자 하는 값

반복문 형태의 insert 함수

• root: 해당 트리의 루트 노드 객체
• val: 삽입하고자 하는 값

# 재귀 형태의 insert 함수
def insert(root, val): # (현재 위치의 노드 객체, 삽입할 값)
    if val < root.val:
        if root.left is None:
            root.left = Node(val)
        else:
            insert(root.left, val)
    elif val > root.val:
        if root.right is None:
            root.right = Node(val)
        else:
            insert(root.right, val)
            
# 반복문 형태의 insert 함수          
def insert(root, val): # (트리의 루트 노드 객체, 삽입할 값)
    cur = root
    while True:    
        if cur.val > val:
            if cur.left is None:
                cur.left = Node(val)
                return
            else:
                cur = cur.left
        elif cur.val < val:
            if cur.right is None:
                cur.right = Node(val)
                return
            else:
                cur = cur.right

풀이2 - 전위 순회 방식에 대한 이해를 바탕으로 전위 순회 배열을 사용해 후위 순회 배열을 생성

전위 순회 방식은 ROOT -> LEFT -> RIGHT 이고, 후위 순회 방식은 LEFT -> RIGHT -> ROOT 이다.
따라서 전위 순회 배열을 사용해 후위 순회 배열을 생성하기 위해 전위 순회 배열에서 LEFT -> RIGHT -> RIGHT 순으로 탐색을 행하면 된다.

방법은 다음과 같다.

ROOT 를 제외한 LEFT, RIGHT 서브트리에 대해 LEFT -> RIGHT 순서로 재귀 순회를 하고, 두 재귀가 끝나면 현재 위치의 ROOT 를 출력해주면 된다. 이렇게 함으로서 전위 순회 배열을 이용해 후위 순회 순서를 구할 수 있게 된다.

이 방법이 문제가 의도한 풀이법인 것 같다.

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

arr = []
while True:
    try:
        arr.append(int(input().strip()))
    except:
        break

def pre_order_to_post_order(start, end):
    if start > end:
         return 
    
    root = arr[start]
    idx = start+1
    # while idx < end and arr[idx] < arr[start]: 이렇게 하면 맨 마지막 값에 대해 검사를 안하게 됨
    while idx <= end and arr[idx] < arr[start]:
        idx+=1

    pre_order_to_post_order(start+1, idx-1) # LEFT
    pre_order_to_post_order(idx, end) # RIGHT
    print(root) # ROOT

pre_order_to_post_order(0, len(arr)-1)

재귀를 사용했을 때 "파이썬"에서 특히 시간 초과가 발생하는 이유

파이선에서 깊은 재귀 호출로 인한 오버헤드가 크기 때문이다.

1. 재귀 호출 = 함수가 호출될 때마다 스택 프레임이 쌓임
파이썬에서 함수가 호출되면 함수 이름, 매개변수 값, 지역 변수, 리턴 주소 등의 정보가 담긴 "스택 프레임(stack frame)"이 생기고, 이게 콜 스택(call stack) 위에 쌓인다.

def f(n):
    if n == 0:
        return
    f(n-1)

이걸 f(10000) 하면, 10000개의 함수 호출 정보가 스택에 쌓인다. 이게 바로 재귀 호출 오버헤드의 핵심이다.

2. 파이썬의 인터프리터 구조 때문에 더 느림
파이썬은 C처럼 컴파일된 언어가 아니라, 인터프리터 언어라서 함수 호출할 때 내부적으로 많은 작업(오브젝트 생성, 스택 관리 등)이 일어난다.

따라서 각 호출마다 프레임 객체 생성 → 메모리 할당 → 프레임 연결 → 추적용 디버그 정보 관리 등의 과정을 수행하기 때문에 함수 하나 호출하는 데에도 부담이 크다.

3. Tail Call Optimization(꼬리 재귀 최적화) 없음

def tail_recursive(n, acc=0):
    if n == 0:
        return acc
    return tail_recursive(n-1, acc+n)

꼬리 재귀 최적화는 마지막 줄에서 자신을 리턴하는 형태인데, 일부 언어는 이걸 스택 쌓지 않고 재사용해서 최적화한다.
그러나 파이썬은 이 최적화를 하지 않는다. 따라서 함수를 호출할 때마다 무조건 스택이 쌓이므로 깊은 재귀는 무조건 성능 손해이다.