Norm

numpy.linalg.norm

a function in NumPy's linear algebra module that computes various types of vector and matrix norms. It is commonly used to measure the magnitude of vectors or matrices in different ways.

Syntax:

numpy.linalg.norm(x, ord=None, axis=None, keepdims=False)

Parameters:

x: the input array (vector or matrix).
ord: The order of the norm (default in None, which gives the Frobenius norm for matices of L2-norm for vectors
axis: specifies which axis to compute the norm along (useful for multi-dimensional arrays).
keepdims: If "True", the result keeps the same dimensions as the input

Common Uses and Norms

1. Eucliden (L2) Norm (Default)

The most commonly used norm is the L2-norm, which is the Euclidean distance:

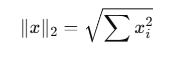
Example:

import numpy as np

x = np.array([3, 4])
norm = np.linalg.norm(x) #default is L2 norm
print(norm) # Output: 5.0 (since sqrt(3^2+4^2) = 5

2. L1 Norm (Manhattan Norm)

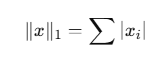
Example:

x = np. array([3, -4])
l1_norm = np.linalg.norm(x,ord=1)
print(l1_norm) # Output: 7 (|3| + |-4|)

3. L∞ Norm (Maximum Norm)

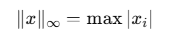
Example:

x = np.array([3, -4, 6])
linf_norm = np.linalg.norm(x, ord=np.inf)
print(linf_norm) # Output: 6 (maximum absolute value)

4. Frobenius Norm (For Matrices)

The Frobenius norm is equivalent to the Euclidean norm but for matrices:

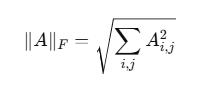
A = np.array([[1, 2], [3, 4]])
frobenius_norm = np.linalg.norm(A)
print(frobenius_norm) # Output: sqrt(1^2 + 2^2 + 3^2 + 4^2) = 5.477

5. Custum Norms (p-Norm)

For a general Lp-norm:

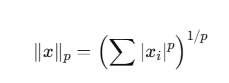
Example for p = 3:

x = np.array([1, -2, 3])
l3_norm = np.linalg.norm(x, ord=3)
print(l3_norm) #Output: (1^3 + 2^3 + 3^3)^(1/3)

Application in Machine Learning & Engineering

• Physics-Informed Machine Learning (PIML): To evaluate error metrcs like relative L2 error.
• **Optimiation: Used in cost functions (e.g., L1 and L2 regularization in machine learning).
• Computational Fluid Dynamics (CFD): To measure numerical solution accuracy.
• Image Processing: To compute differences between images.