테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
정사각형은 서로 겹치면 안 된다.
도형은 모두 연결되어 있어야 한다.
정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.
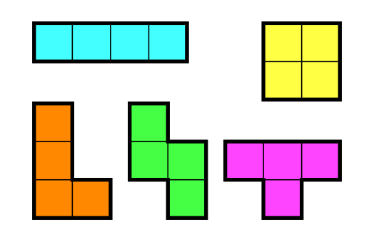
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.
import sys
import copy
sys.stdin = open("input.text", "rt")
n,m = map(int, input().split())
g = [list(map(int, input().split())) for _ in range(n)] #nxm
dx = [-1,0,1,0]
dy = [0,1,0,-1] #북 동 남 서
#ㅗ 제외 모두 탐색 가능
res = -2424242424
temp = []
def DFS(L, x, y, sum):
global res
if L == 3: #3개 선택 완료. 종료조건
# print(temp)
res = max(res, sum)
else:
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0<=nx<n and 0<=ny<m: #경계선 안에
if ch[nx][ny] == 0: #방문 안했다면
if L == 1: #2개 선택한 시점에 ㅗ자 고려
ch[nx][ny] = 1
DFS(L+1, x,y,sum + g[nx][ny])
ch[nx][ny] = 0
ch[nx][ny] = 1
DFS(L+1, nx,ny,sum + g[nx][ny])
ch[nx][ny] = 0 #백트랙킹 시 원상복구
ch = [[0] * m for _ in range(n)] #방문 체크를 위한 리스트
#이제 ㅗ자형 따로 구해야함
def cal(x,y):
global res
for i in range(4): #시작 방향설정.
sum_data = g[x][y] #초기값 설정
for k in range(3):
d = (i+k) % 4
nx = x + dx[d]
ny = y + dy[d]
if not (0<=nx<n and 0<=ny<m):
break
sum_data += g[nx][ny]
res = max(res, sum_data)
for i in range(n):
for j in range(m):
ch[i][j] = 1 #시작 지점 역시 방문처리하고 들어가야해
DFS(0, i,j,g[i][j])
ch[i][j] = 0
# cal(i,j)
print(res)👻 코멘트
해당 문제는 현재좌표 기준 DFS로 총 3번 들어가면 (상태트리 구현) 원하는 테트리스 4개짜리가 나온다. 하지만 ㅗ자 유형은 따로 예외처리?를 해줘야만 구현할 수 있다...
- DFS + 구현 유형을 문제를 읽으면서 파악했어야함
여튼 현 좌표 기준 DFS로 상하좌우 돌아가면서 4개의 블럭을 완성하면 거기의 sum값이 최대인지 확인. 그리고 ㅗ자 따로 확인. 이 아이디어만 잘 구현했다면 풀 수 있었던 문제...
😀 ㅗ자는 블럭의 크기가 2일 때 새로운 블럭으로 (좌표이동) 탐색하는 것이 아니라 기존 블럭에서 다시 탐색을 한다면 ㅗ자를 구현할 수 있다. (물론 따로 함수 구현해서 ㅗ자 유형만을 탐색해도 됨)
