Graph search
Graph search 에 대해 알아봅시다. 가 주어졌을때 목표는 모든 정점과 간선을 탐색하는 것 입니다.
궁극적으로는 그래프의 정점과 간선을 탐색하면서, 그래프에서 발견된 연결된 정점들로 트리를 구성합니다.
Graph search의 예시로는 BFS와 DFS가 있습니다.
BFS (Breadth-first Search)
BFS는 너비 우선 탐색으로 그래프 탐색에 이용됩니다.
큐의 FIFO(First In First Out) 성질을 이용하여 정점들을 차례로 탐색합니다.
기본적으로 가까운 노드부터 우선적으로 탐색하며, 두 노드사이의 최단 경로 를 찾고자 할때 주로 사용됩니다.
BFS 동작과정
동작과정은 아래와 같습니다.
-
시작 정점으로부터 가장 가까운 정점을 먼저 방문합니다.
-
시작 정점을 지나고 나면 깊이가 1인 모든 정점을 방문하고, 그 다음에는 깊이가 2인 모든 정점을 방문합니다.
-
이런식으로 한단계씩 깊이를 더해가며 해당 깊이에 있는 모든 정점들을 방문해 나가다가 더 이상 방문할 곳이 없을때 탐색을 종료합니다.
즉, 첫번째로 들어간 정점을 기준으로 그와 인접한 모든 정점을 탐색한 뒤, 인접정점들의 자식정점으로 탐색을 확장해나가며 더이상 방문할 곳이 없을때까지 반복합니다.
그래프 탐색을 할 때에는 노드 탐색의 효율성과 무한루프 방지를 위해 어떤 노드를 방문했었는지 여부를 반드시 검사해줘야 합니다.
알고리즘 관점에서는 이러한 탐색 과정을 나타내기 위해 세가지 색으로 표현하고, 코드로 구현할 때에는 방문 배열을 선언하여 T/F 혹은 0,1,2로 표현해줍니다.
Vertex Colors
- white : 아직 발견되지 않은 정점
- gray : 발견되었지만 아직 완전히 탐색되지 않은 정점
- black : 발견되고 완전히 탐색된 정점
위의 내용을 짧게 정리하면 아래와 같습니다.
BFS 특징
- 너비 우선 탐색
- 큐의 FIFO(First In First Out) 성질을 이용하여 정점들을 차례로 탐색합니다.
- 그래프 탐색의 경우, 어떤 노드를 방문했는지 여부를 반드시 검사해야합니다.
- 재귀적으로 동작하지 않습니다.
pseudo code
BFS(G, s)
for each u ∈ V - {s} do
color[u] ← WHITE
Π[u] ← NIL
d[u] ← ∞
color[s] ← GRAY
Π[s] ← NIL
d[s] ← 0
Q ← {s}
while Q ≠ ∅ do
u ← head[Q]
for each v in Adj[u] do
if color[v] = WHITE then
color[v] ← GRAY
Π[v] ← u
d[v] ← d[u] + 1
ENQUEUE(Q, v)
DEQUEUE(Q)
color[u] ← BLACK
BFS Example(undirected)
그림을 통해 이해해봅시다.
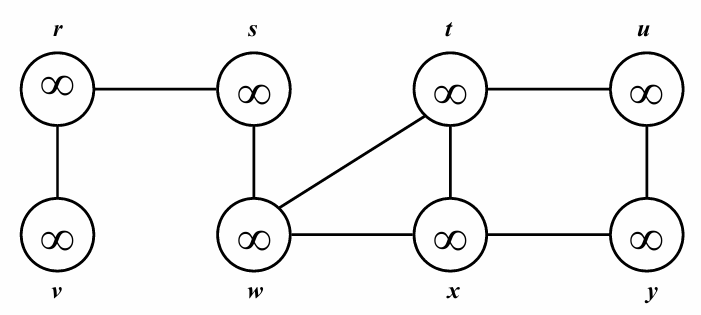
아래와 같이 모든 정점이 방문하기 전인 무방향 그래프가 있습니다.
모든 정점이 아직 방문하기 전이므로, 정점의 색이 모두 white임을 확인할 수 있습니다.
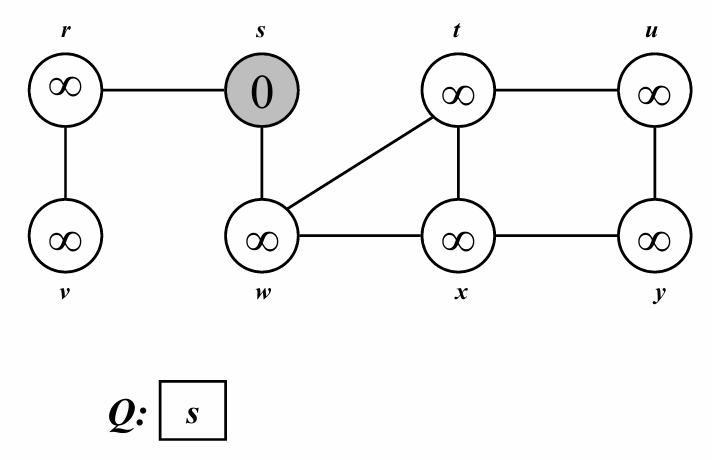
s를 시작정점으로 하기 위해 큐에 s를 넣어준 것을 확인할 수 있습니다.
아직 탐색 전이고 회색으로 색칠한것을 확인할 수 있습니다.
이때, 시작 정점 s의 depth = 0입니다.
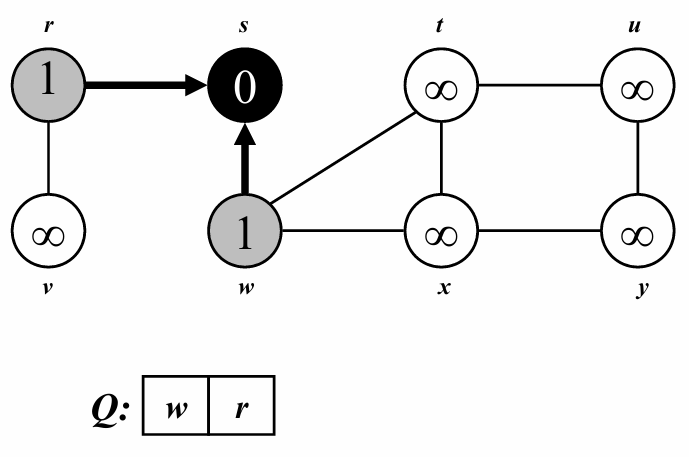
이후, 큐에서 정점 s를 꺼내어 탐색을 시작합니다.
s에 인접한 정점 r과 w 에 대해 아직 탐색하지 않은 상태이므로, gray(탐색 중) 상태로 변경해줍니다.
이후, r과 w의 부모를 s로 설정해주고, r과 w의 거리를 s보다 1 더한 값으로 변경해줍니다.
모든 준비가 완료되었으므로, 큐에 정점 r과 w를 넣어줍니다. 이는 다음에 탐색할 정점으로 등록한것과 동일합니다.
s의 모든 인접 정점 r과 w를 탐색 완료했으므로, 큐에서 s를 제거해주고, s의 색을 검정색으로 변경해줍니다.
위의 과정을 거친 이후 아래 그림과 같이, 정점 s는 검정색, 인접 정점 r와 w는 s를 부모로 가리키고 있고, r과 w은 탐색할 준비를 마쳤으므로 큐에 존재하고, 정점의 색은 따라서 회색인것을 확인할 수 있습니다.
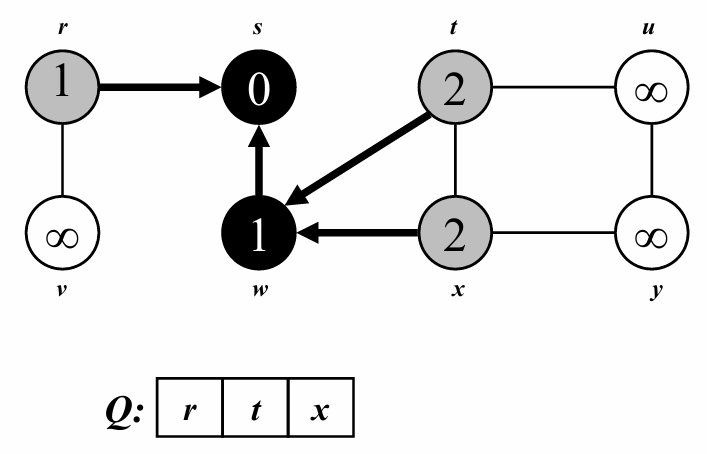
위의 과정을 반복해줍니다.
다음 정점은 r이 됩니다.
정점 r의 인접 정점인 t와 x는 아직 방문되지 않았으므로 회색(탐색 중)으로 바꾸고, 부모를 r로 설정한 뒤 큐에 추가합니다.
이후 w의 모든 인접 정점을 탐색했으므로, 큐에서 w를 제거해준 이후에 black으로 바꾸어줍니다.
depth는 아까보다 1증가해 2로 변경된것을 확인할 수 있습니다.
위의 과정을 큐에 아무것도 남아있지 않을 때 까지 반복해줍니다.
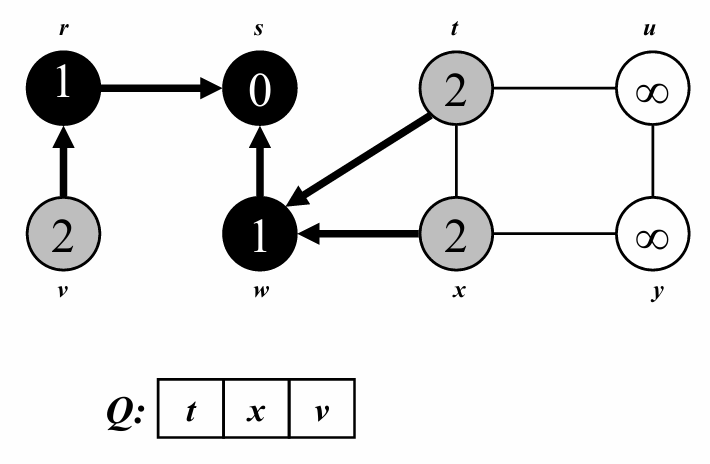
depth=2 인 모든 정점을 큐의 순서대로 탐색해줍니다.
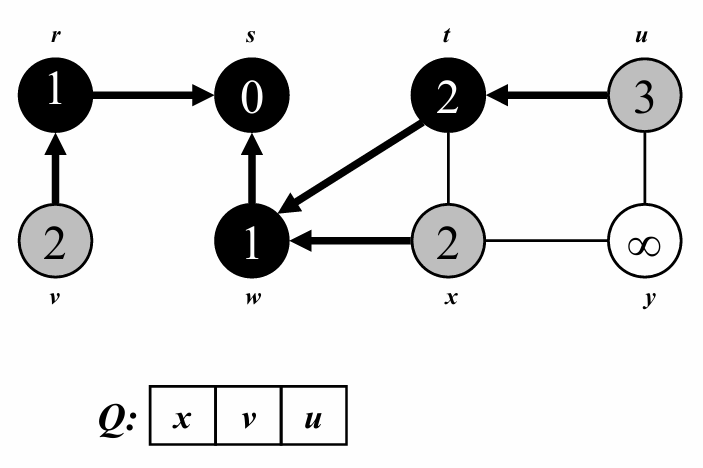
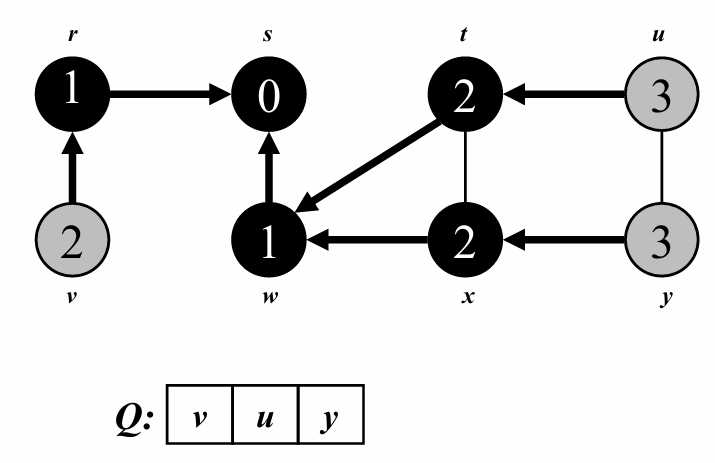
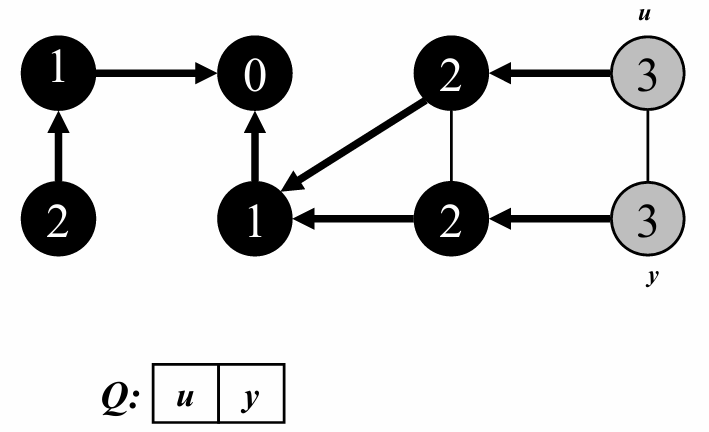
이제 depth = 3인 정점에 대해 탐색해줍니다.
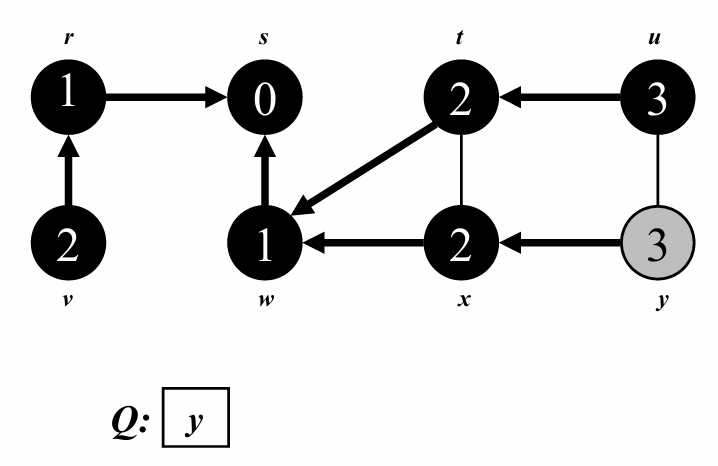
모든 정점이 탐색되었고, 큐가 비었으므로 탐색을 종료합니다.
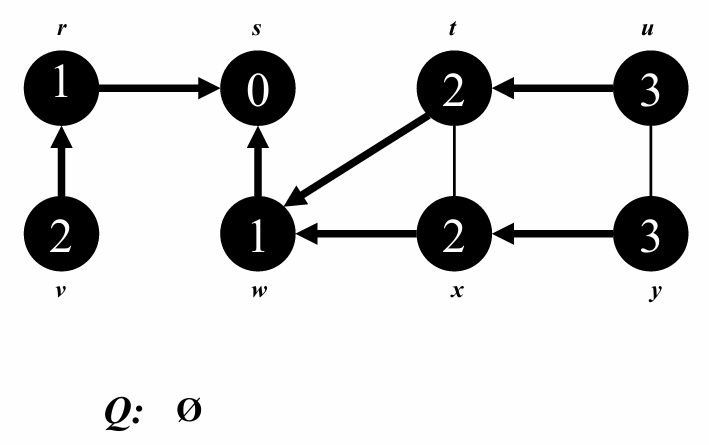
BFS Example(directed)
BFS는 방향그래프에서도 사용할 수 있습니다.
임의의 정점 s를 큐에서 꺼내어주고 a를 인접 정점으로 지정해줍니다.
a를 gray로 설정해주고 큐에 넣어준것을 확인할 수 있습니다.
a를 root으로 봤을때 정점 a의 depth = 0인 것을 확인할 수 있습니다.
a의 인접정점을 모두 탐색하여 부모를 설정하고 거리를 설정합니다.
다음과 같이 보라색이 된 것을 확인할 수 있습니다.
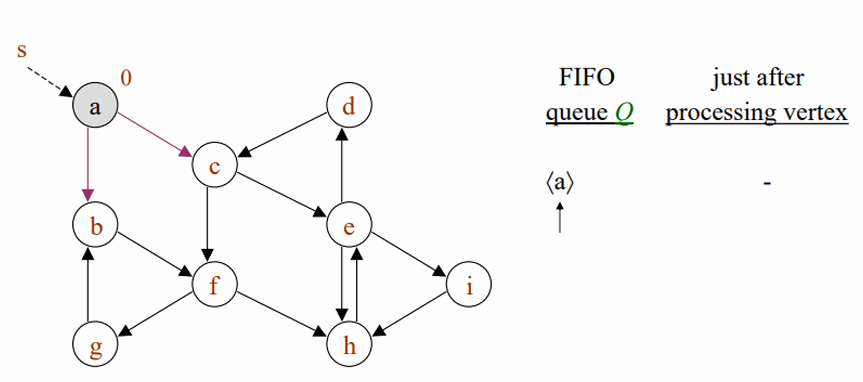
a의 인접정점을 모두 탐색해주었으므로, a를 black으로 설정하고, 인접정점들은 gray(탐색 중) 상태로 변경해줍니다. 부모를 a로 설정하고 depth=1로 설정해줍니다.
이후, 정점 b에 해당하는 인접정점은 f입니다.
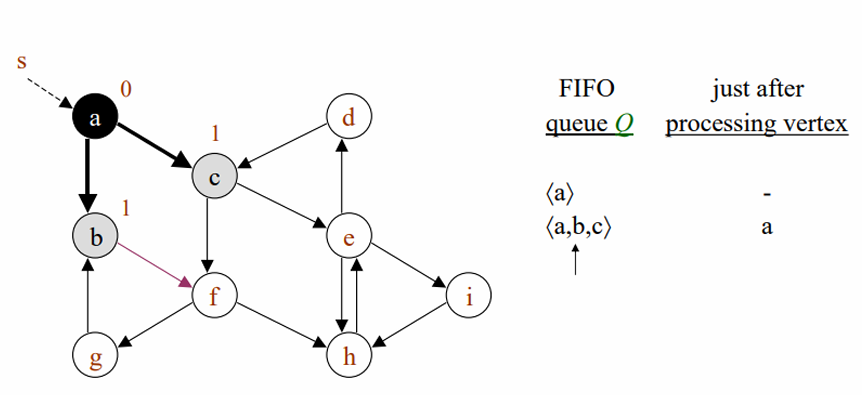
정점 f를 gray로 변경하고, 부모포인터를 b로 설정해주고, depth=2 로 설정해줍니다.
b의 모든 인접 정점에 대해 탐색을 완료해주었으므로, b를 큐에서 꺼낸 이후, black으로 변경해줍니다.
c의 인접정점은 f와 e입니다.
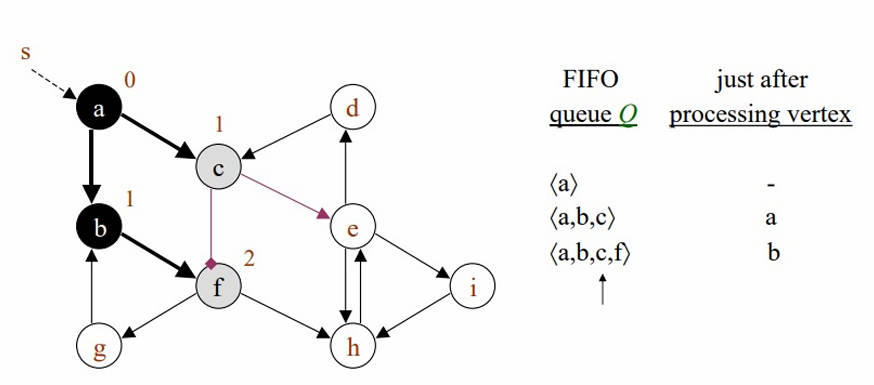
동일한 과정을 거쳐 부모포인터와 debth를 설정해주고 색을 gray로 변경해줍니다.
c의 모든 인접정점을 방문했으므로, c를 큐에서 꺼내어 black으로 변경해줍니다.
위의 과정을 계속해서 반복합니다.
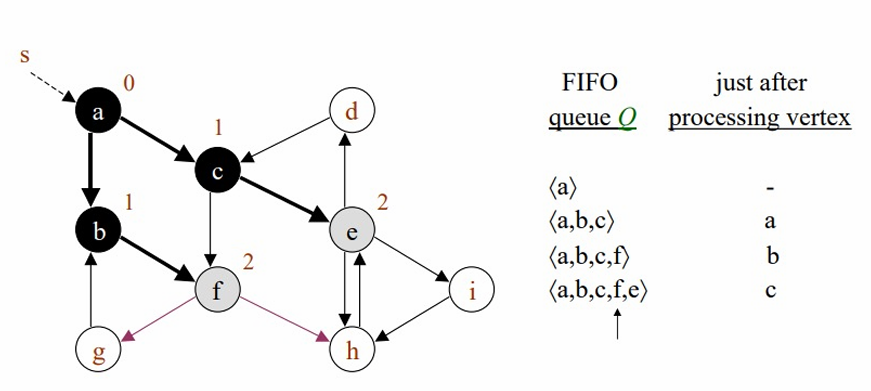
debth = 2
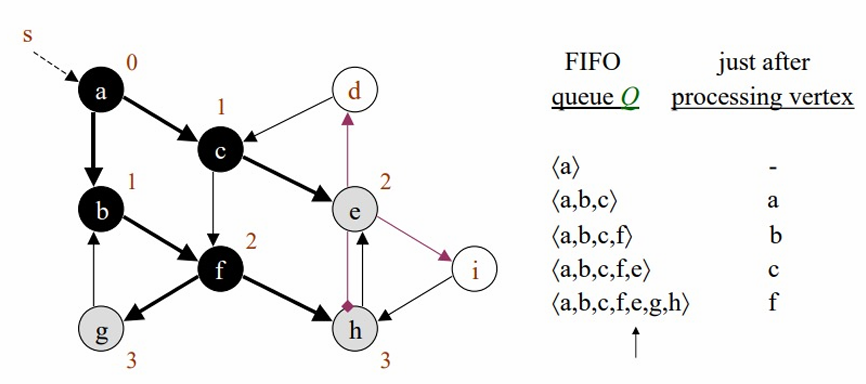
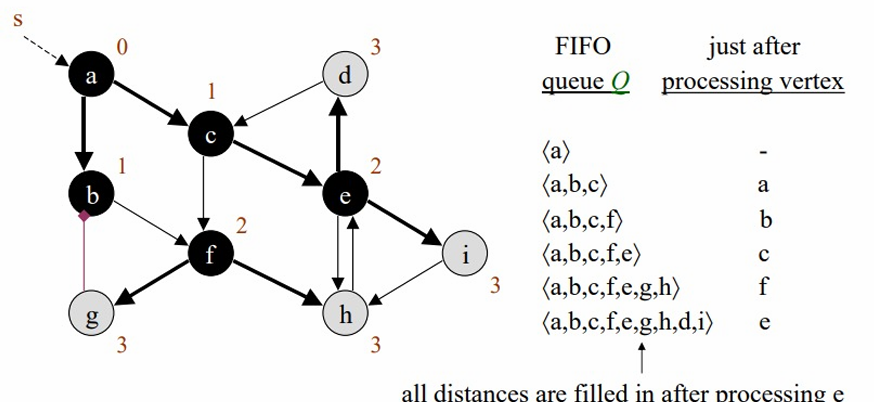
debth = 3
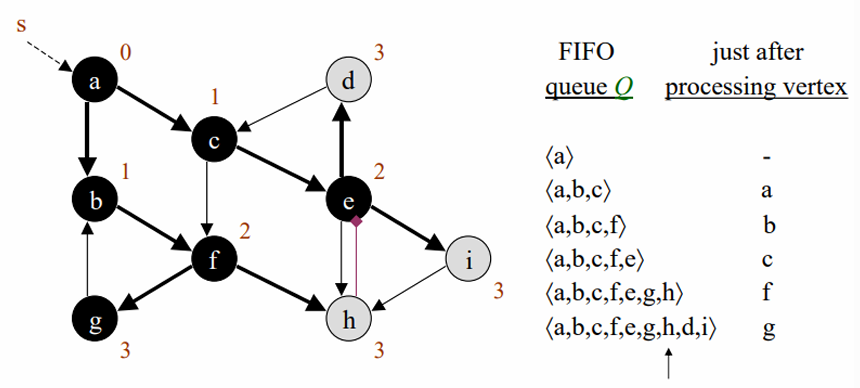
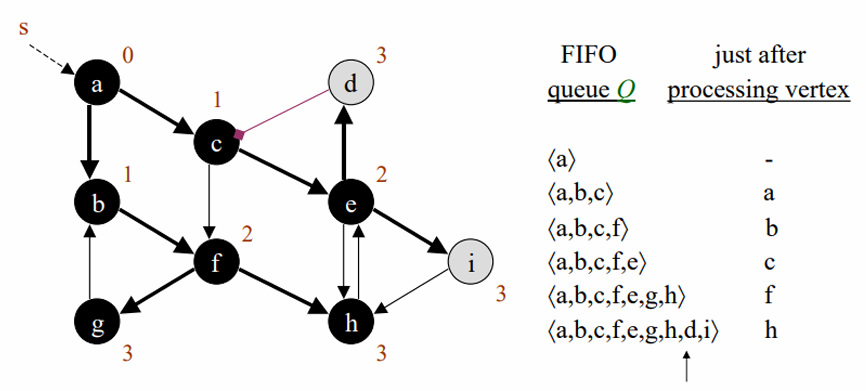
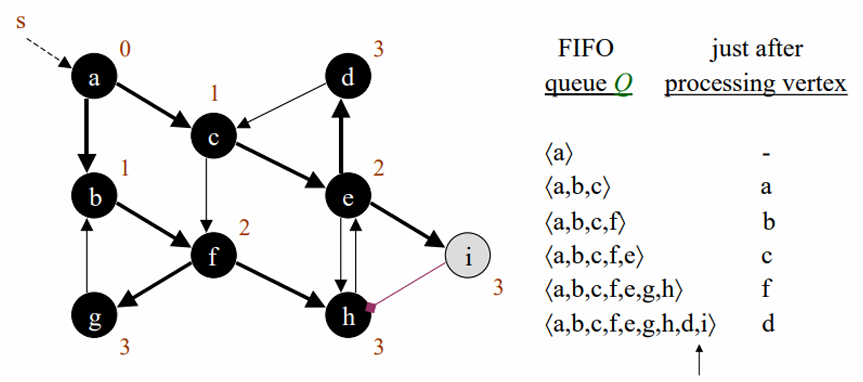
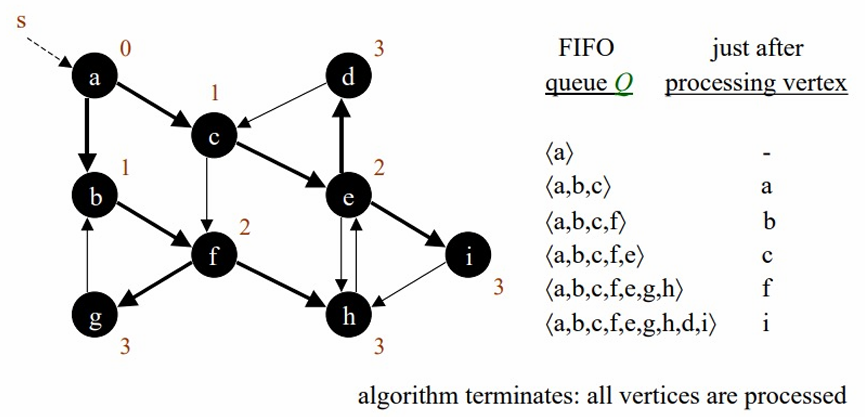
모든 노드를 방문할때까지 방문해줍니다.
BFS가 종료된 이후에는 tree가 생성됩니다.
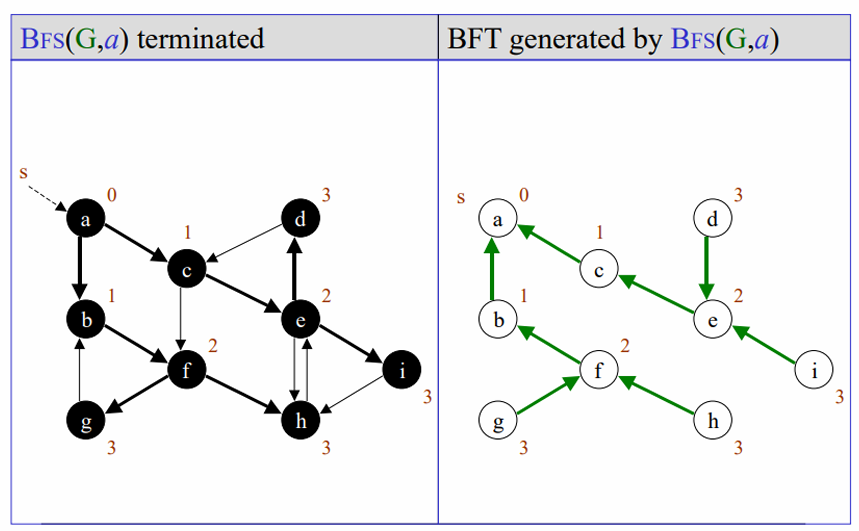
BFS 시간 복잡도
BFS의 시간복잡도는 그래프의 정점 수와 간선 수에 따라 결정됩니다.
-
초기화 작업: 모든 정점을 WHITE로 초기화하는 작업은 입니다. 모든 정점이 반드시 한 번씩 초기화되므로 정점의 수만큼 일정하게 소요됩니다.
-
큐 작업: 각 정점은 큐에 한 번 삽입(enqueue)되고, 한 번 제거(dequeue)되므로 큐 작업의 시간 복잡도는 입니다. 큐에서의 삽입과 제거는 모두 상수 시간인 O(1) 에 이루어지기 때문에 정점의 수에 비례하는 시간 복잡도를 갖습니다.
-
회색 정점 처리: 각 정점이 한 번 탐색될 때마다 인접한 정점을 모두 확인해야 하므로, 이 작업은 간선의 수 에 비례합니다. 모든 간선은 한 번만 처리되므로 의 시간 복잡도를 갖습니다.
최종 시간 복잡도
따라서 BFS의 전체 시간 복잡도는 입니다. 이 복잡도는 그래프를 선형적으로 탐색할 때 발생하는 전형적인 복잡도입니다.
