Graphs
Graph G = (V,E)
- 이때, V는 정점(Vertices)의 집합, E는 간선(Edges)의 집합을 의미하며, E는 V×V의 부분집합입니다.
- 간선의 크기는 의 점근적 상한을 공간 복잡도로 가집니다.
모든 정점에 간선이 연결되어 있는 밀집 그래프(dense graph) 일 수 있고, 적게 연결되어 있는 트리나 희소 그래프(sparse graph) 일 수도 있습니다.
간선의 방향성 유무에 따라 그래프는 다음과 같이 나눌 수 있습니다.
Directed Graphs
그래프에서 간선은 벡터처럼 방향성을 가지고 있을 수 있습니다.
예를들어, Edge(u,v) 과 Edge(v,u)는 방향이 반대이므로 서로 다른 간선이라고 생각하면 됩니다.
Undirected Graphs
스칼라처럼 방향성이 없을수도 있습니다. Edge(u,v)와 Edge(v,u)은 같은 간선이라고 볼 수 있습니다.
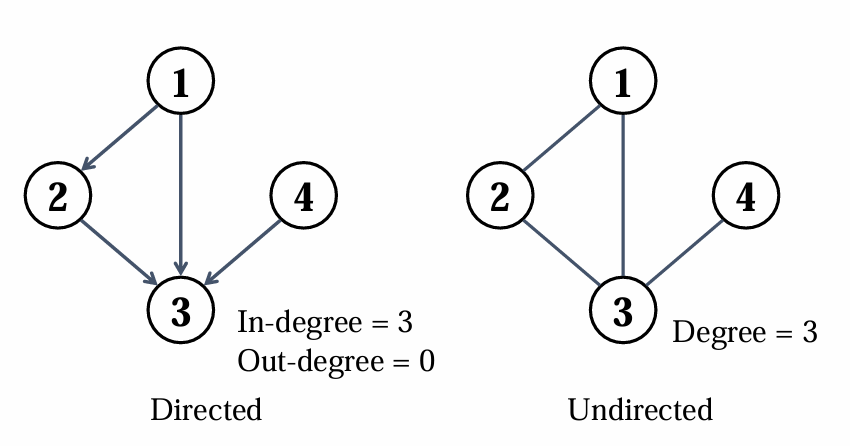
그래프에서 정점의 degree를 구할 수 있습니다.
degree는, 정점v에 인접한 간선의 갯수를 의미합니다.
- 방향성이 있는 directed graph 경우에, degree를 In-degree와 out-degree으로 나눌 수 있습니다.
- 방향성이 없는 undirected graph 경우엔 in과 out을 구분짓지 않습니다.

위의 사진을 에시로 들어봅시다.
-
Directed graph에서 정점3을 기준으로 차수를 구해봅시다.
정점 1,2,4가 정점 3을 향해있는것을 볼 수 있고, 정점3에서 나가는 간선은 없는것을 확인할 수 있습니다.
따라서, In-degree는 3, out-degree는 0입니다. -
undirected graph에서 정점3에 연결되어있는 정점은 1,2,4으로 세개입니다.
따라서, Degree는 3입니다.
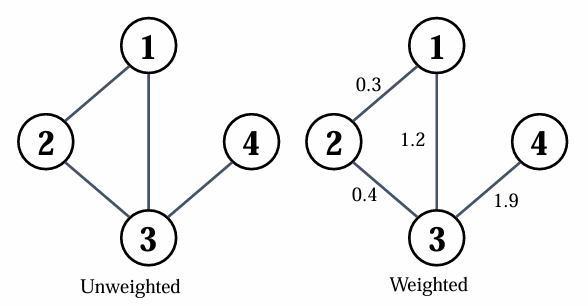
간선에는 가중치가 존재할 수 있습니다.
Weighted, Unweighted Graphs
Representing Graphs_Matrix
그래프를 행렬로 표현할 수 있습니다. 인접행렬은 그래프에서 정접간의 연결관계를 나타내는 방식으로, x 크기의 2차원 배열로 그래프를 표현합니다.
예시를 통해 알아보겠습니다.
Directed, unweighted graph
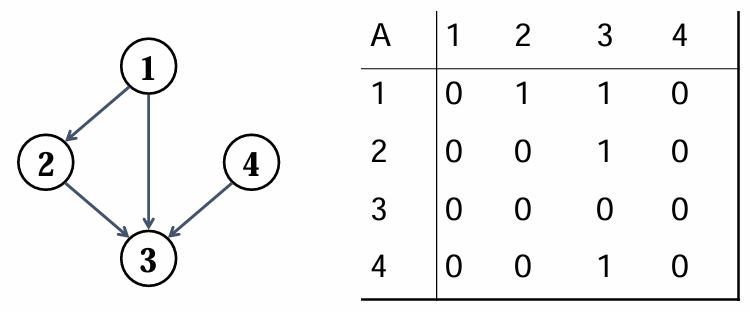
좌측의 그래프는 유향, 무가중치 그래프입니다.
정점은 1,2,3,4 간선은 (1,2), (2,3), (1,3), (4,3) 으로 주어져 있습니다.
이를 행렬로 표현하면 우측의 행렬과 같습니다.
각 간선에 대한 가중치가 없는 경우, 연결되어있으면 1, 연결되어있지 않으면 0으로 표현합니다.
undirected, unweighted graph
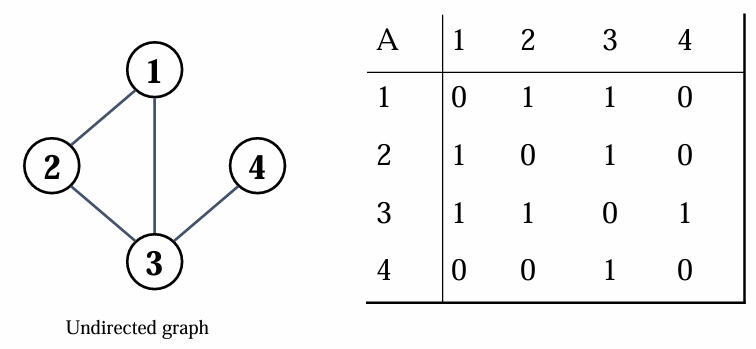
다음은 방향이 없고 간선에 대한 가중치도 없는 그래프의 경우입니다.
방향이 없는 그래프의 경우, (u,v) = (v,u) 이므로 행렬은 대칭행렬입니다.
또한, 가중치가 존재하지 않으므로 1과 0으로 표현된 이진행렬입니다.
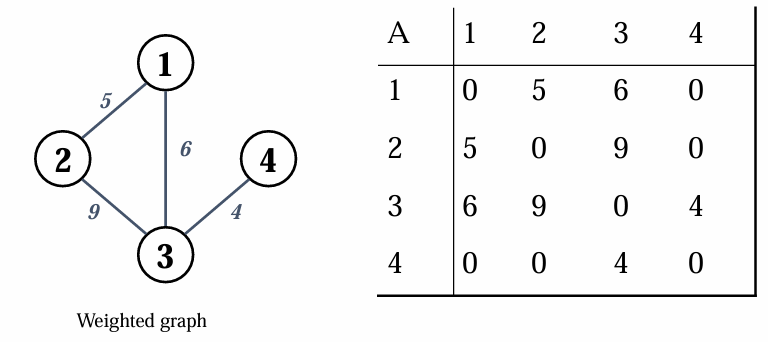
undirected, weighted graph
다음의 경우는 방향이 없고 가중치가 존재하는 그래프의 경우입니다.
간선의 가중치가 존재하면,각 간선의 가중치에 해당하는 값을 행렬에 써주면 됩니다.
이 경우에도, (u,v) = (v,u) 이므로 행렬은 대칭행렬입니다.
Representing Graphs_List
그래프를 리스트의 형태로 표현할 수도 있습니다. 그래프의 각 정점에 연결된 다른 정점들을 리스트 형식으로 저장한 자료구조입니다.
Directed, unweighted graph
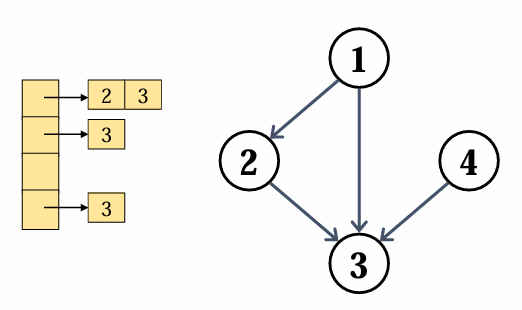
Adj[1] ={2,3}
Adj[2] ={3}
Adj[3] ={}
Adj[4] ={3}
인덱스에 정점이 들어가고, 각각에는 각 정점에 연결된 다른 정점들을 리스트 형식으로 저장하고 있습니다.
undirected, unweighted graph
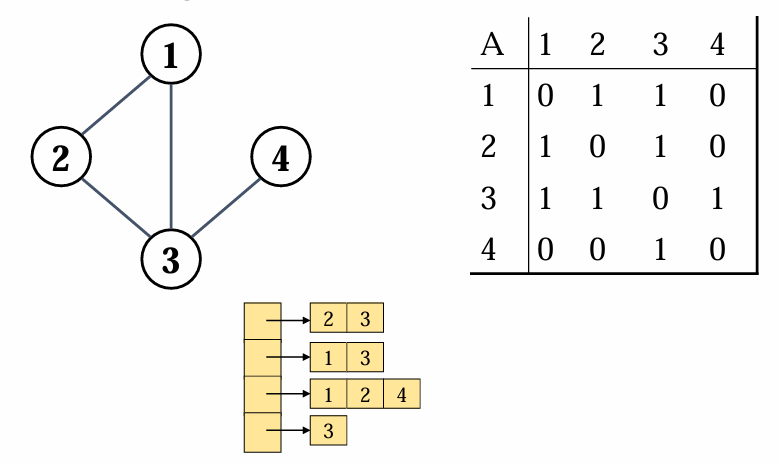
Adj[1] ={2,3}
Adj[2] ={1,3}
Adj[3] ={1,2,4}
Adj[4] ={3}
방향이 없는 경우에는, (u,v) = (v,u)이므로 간선이 중복되어 앞의 경우와 비교했을때 간선의 갯수가 두배인것을 확인할 수 있습니다.
undirected, weighted graph
가중치가 있는 경우, 정점과 간선의 가중치의 pair을 적어주면 됩니다.
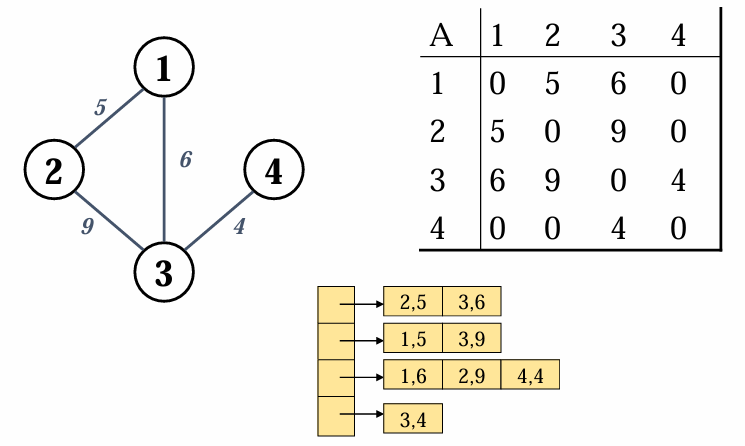
Adj[1] ={(2,5),(3,6)}
Adj[2] ={(1,5),(3,9)}
Adj[3] ={(1,6),(2,9),(4,4)}
Adj[4] ={3,4}
Storage?
리스트가 차지하는 공간은 어떻게 될까요 ?
directed graph
directed graph 같은 경우에는, 각 정점에 대해 만큼 차지합니다.
따라서, 리스트의 총 크기는 이고 와 동일합니다.
undirected graph
undirected graph의 경우에는 각 정점에 대해 만큼 차지합니다.
리스트의 총 크기는 이고, 이는 간선의 집합 크기의 두배인 와 동일합니다. (방향이 없으니 간선갯수에 두배해주면 됩니다)
(directed)리스트의 총 크기 = sum of out-degree(v) = |E|
(undirected)리스트의 총 크기 = sum of degree(v) = 2*|E|
따라서, 각 정점이 가지고 있는 리스트의 주소를 저장하는 V개의 공간과, 인접리스트 자체의 공간을 포함해서 공간복잡도를 가집니다.
Matrix vs List
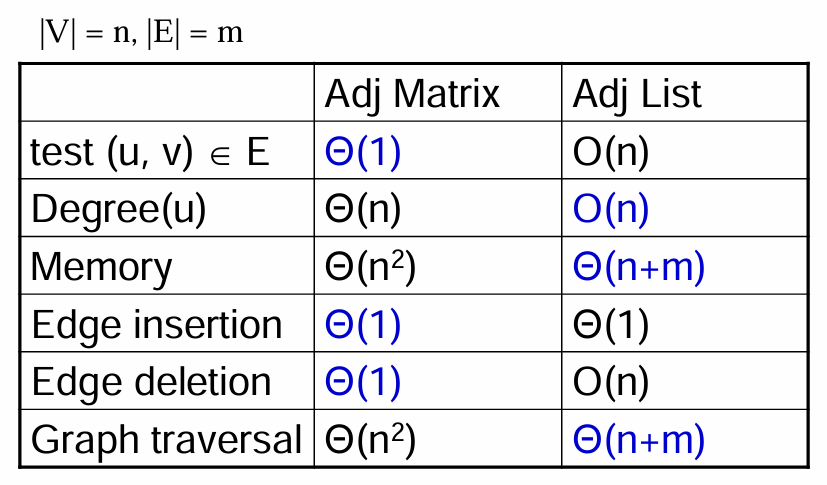
둘의 차이는 위의 표와 같습니다.
