[algorithm] Quicksort, partition(Hoare, Lomuto)

현굥·2024년 8월 4일

algorithm

목록 보기

9/17

Quicksort

Quicksort 분할 정복 알고리즘입니다.
'in place'정렬 알고리즘으로, 병합 정렬과 달리 추가적인 메모리 공간을 많이 사용하지 않습니다.

Quicksort 의 시간복잡도

평균적을 $O(nlogn)$ 의 시간복잡도를 가지며, 최악의 경우, $O(n^2)$ 의 시간복잡도를 가집니다.

Quicksort는 다음의 과정을 거칩니다.

Quicksort_ 분할정복기법

Divide : 배열을 Pivot $x$ 값을 중심으로 두개의 하위배열로 분할합니다. 하위 배열의 모든 요소는 피봇보다 작거나 같고, 다른 상위 배열의 모든 요소는 피봇보다 크거나 같습니다.
Conquer : 두 하위배열을 재귀적으로 정렬합니다.
- Quicksort의 Partition과정에서 이미 배열이 피봇을 기준으로 정렬되었고, 각 재귀 호출 이후에는 이미 요소들이 올바른 위치에 배치되므로, combine의 과정은 필요하지 않습니다.

Quicksort_Pseudo Code

QUICKSORT(A, p, r)
if p < r
    then q ← PARTITION(A, p, r)
    QUICKSORT(A, p, q-1)
    QUICKSORT(A, q+1, r)

Quicksort_Partition()

Quicksort의 핵심은 Partition 단계에 있습니다. Partition 함수는 배열을 피벗을 기준으로 두 부분 배열로 나누고, 각각의 부분 배열이 피벗을 기준으로 정렬되도록 합니다.

추가적인 메모리 공간을 사용하지 않고, 주어진 배열 내에서, 즉 제자리에서(in-place) 요소들의 위치를 변경하여 정렬을 수행합니다.
함수 호출 이후, 두개의 하위배열이 생성됩니다.
- 첫 번째 하위 배열은 피벗 값 이하의 값, 두 번째 하위 배열은 피벗 값 이상의 값들로 구성됩니다.
- 이때, Pivot의 인덱스를 반환하여 두 하위 배열을 구분합니다.
Partition 알고리즘에는 대표적으로 Hoare's 알고리즘과, Lumuto's알고리즘이 존재합니다.

Hoare's Partitioning Algorithm

Hoare의 파티셔닝 알고리즘은 피벗 주위로 배열을 두 부분으로 나누는 과정을 수행합니다.

피벗 요소 선택: $pivot = x = A[p]$
시간 복잡도: 배열의 모든 요소를 한 번씩 비교하고 교환하기 때문에 $O(n)$ 의 시간복잡도를 가집니다.

code

H-PARTITION(A, p, r)
    pivot ← A[p]
    i ← p
    j ← r + 1
    while true do
        repeat j ← j - 1 until A[j] ≤ pivot
        repeat i ← i + 1 until A[i] ≥ pivot
        if i < j then
            exchange A[i] ↔ A[j]
        else
            return j

그림을 통해 설명해보겠습니다.

파란색 구간 [p,i-1]: 피봇보다 작거나 같은 값들이 위치하는 구간
빨간색 구간 [j+1,r]: 피봇보다 크거나 같은 값들이 위치하는 구간
초록색 구간 [i,j]: 아직 정렬되지 않은 요소들이 위치하는 구간

i는 왼쪽에서 오른쪽으로 이동하며 피봇보다 큰 요소를 찾고, j는 오른쪽에서 왼쪽으로 이동하며 피봇보다 작은 요소를 찾습니다. 이 과정은 알고리즘이 진행됨에 따라 점차 작아집니다.

동작 원리

피벗 선택:
배열 $A[p...r]$ 에서 피벗 요소를 선택합니다.
$pivot = A[p]$
두 영역으로 분할:
A[p...i]는 왼쪽에서 오른쪽으로 확장됩니다.
$A[p...i]\ from\ left\ to\ right$
A[j...r]는 오른쪽에서 왼쪽으로 확장됩니다.
$A[j...r]\ from\ left\ to\ left$

영역 확장 조건:
왼쪽 영역의 모든 요소는 피벗보다 작거나 같아야 합니다.
$every\ element\ in\ A[p...i]\ is ≤ pivot$
오른쪽 영역의 모든 요소는 피벗보다 크거나 같아야 합니다.
$every\ element\ in\ A[j...r]\ is ≥ pivot$

두개의 포인터를 사용하여, i는 배열의 왼쪽에서 오른쪽으로 이동하며 피봇보다 큰 요소를 찾고, j는 배열의 오른쪽에서 왼쪽으로 이동하며 피봇보다 작은 요소를 찾습니다.

영역 확장

i < j 인 동안 포인터를 이동하며 요소를 교환합니다. 이 조건이 만족되는 동안에는 계속해서 교환합니다.
즉, 두 부분배열은 $A[i] ≥ pivot ≥ A[j]$ 가 될 때까지 확장됩니다.

교환
A[i]가 왼쪽 영역에 속하기에는 너무 큽니다.
A[j]가 오른쪽 영역에 속하기에는 너무 작습니다.
i와 j가 교차되는 순간, 반복을 종료하고 j의 위치를 새로운 피봇의 위치로 반환합니다.

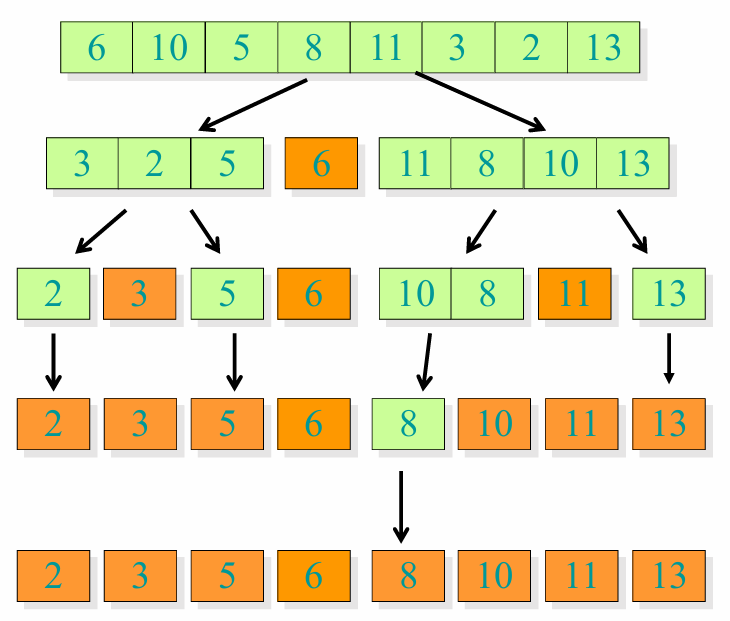
예시를 통해 이해해봅시다.

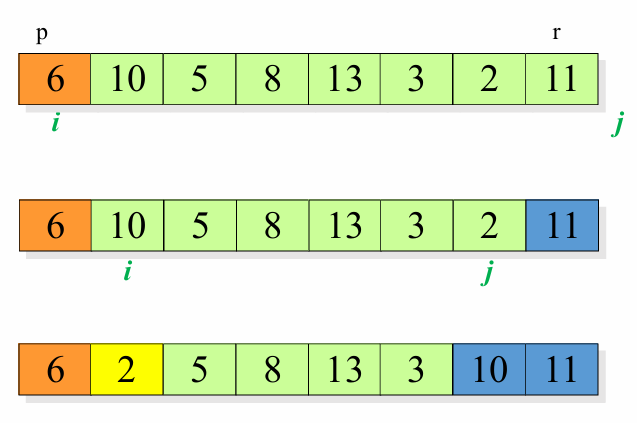
피봇의 값을 배열의 첫번째 원소인 6으로 설정했습니다.
i와 j를 좁혀오며, 값의 크기 비교 이후 값들을 서로 바꿉니다.
위의 과정을 두 값의 크기가 교차될 때 까지 반복합니다.

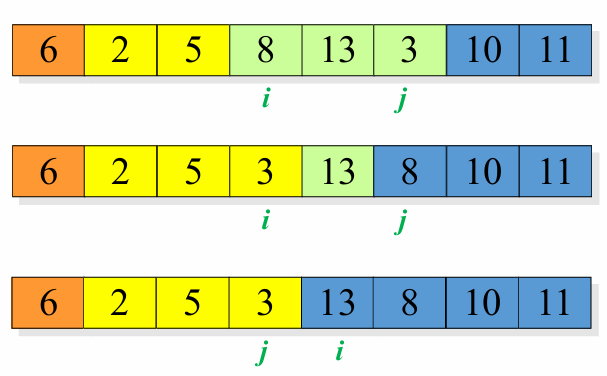
i와 j의 위치가 교차될 때의 j의 위치를 피봇의 위치와 바꿉니다.

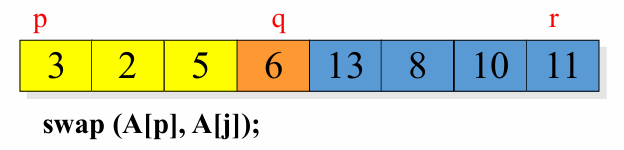
그 결과, 아래의 사진처럼 새로운 피봇과 두개의 부분배열이 생성되었습니다.

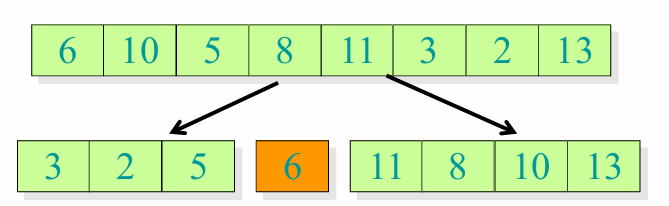
그 다음 부분배열마다 각각의 과정을 반복하면 아래와 같이 정렬된 배열의 모습을 확인할 수 있습니다.

Lomuto's Partitioning Algorithm

Lomuto의 파티셔닝 알고리즘은 피봇 주위로 배열을 두 부분으로 나누는 간단한 방법입니다.

Lomuto의 파티셔닝 알고리즘의 경우 일반적으로 배열의 마지막 요소를 피봇으로 선택합니다.
배열의 모든 요소를 한 번씩 비교하고 교환하기 때문에 $O(n)$ 의 시간복잡도를 가집니다.

code

L-PARTITION(A, p, r)
    pivot ← A[r]
    i ← p - 1
    for j ← p to r - 1 do
        if A[j] ≤ pivot then
            i ← i + 1
            exchange A[i] ↔ A[j]
    exchange A[i + 1] ↔ A[r]
    return i + 1

A: 정렬하려는 배열.
p: 배열의 시작 인덱스.
r: 배열의 끝 인덱스.

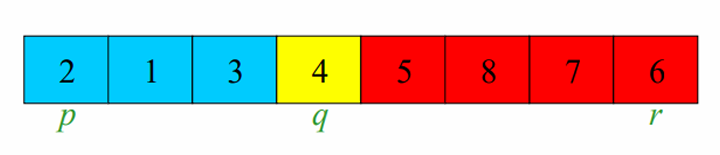
파란색 구간 [p,i]: 피봇보다 작거나 같은 값들이 위치하는 구간
빨간색 구간 [i+1,j-1]: 피봇보다 큰 값들이 위치하는 구간
초록색 구간 [j,r-1]: 아직 정렬되지 않은 요소들이 위치하는 구간
노란색 요소: 현재 피봇 요소

Lomuto 알고리즘은 배열의 끝 요소를 피봇으로 선택하고, 피봇보다 작은 요소들을 앞으로 이동시킵니다. 마지막으로 피봇을 올바른 위치로 이동시킵니다.

동작 원리

A: 정렬하려는 배열.
p: 배열의 시작 인덱스.
r: 배열의 끝 인덱스.

이 함수는 배열 $A[p...r]$ 을 피봇을 기준으로 두 부분으로 나눕니다.

1. 피봇 선택

배열 $A[p...r]$ 에서 피벗 요소를 선택합니다.
$pivot=A[r]$

2. 두 영역으로 분할

$A[p...i]$ 는 피봇보다 작거나 같은 값들이 위치하는 구간입니다.

$A[p...i] is ≤pivot$
$A[i+1...j-1]$ 는 피봇보다 큰 값들이 위치하는 구간입니다.

$A[i+1...j−1] is >pivot$

3. 영역 확장

j가 배열의 끝까지 이동하면서 A[j]가 피봇보다 작거나 같으면 i를 증가시키고 A[i]와 A[j]를 교환합니다.

4. 피봇 위치 조정

최종적으로 A[i+1]과 피봇 요소 A[r]를 교환하여 피봇을 올바른 위치로 이동시킵니다.

5. 반환

i+1 위치를 반환하여 피봇의 최종 위치를 알려줍니다.

예시를 통해 알아봅시다.

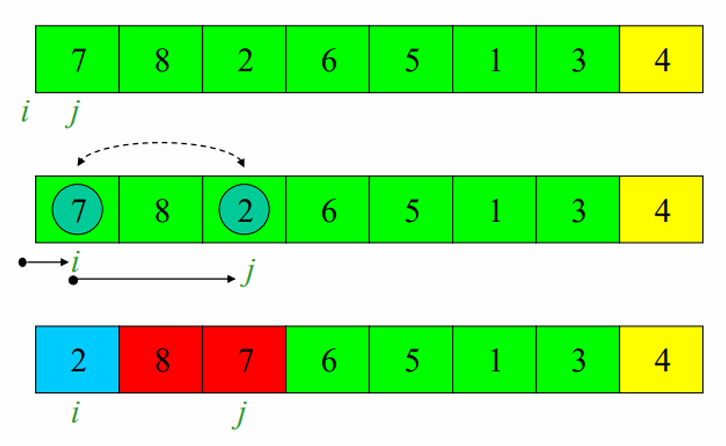
배열의 맨 마지막 원소 4를 피봇으로 설정합니다.
j를 늘려가면서, 피봇의 값과 비교합니다.
A[j] ≤ pivot 인 경우에, i의 값을 하나 늘리고, A[i] ↔ A[j] 해줍니다.
이후, 다시 j를 늘려가며 피봇의 값과 비교합니다.

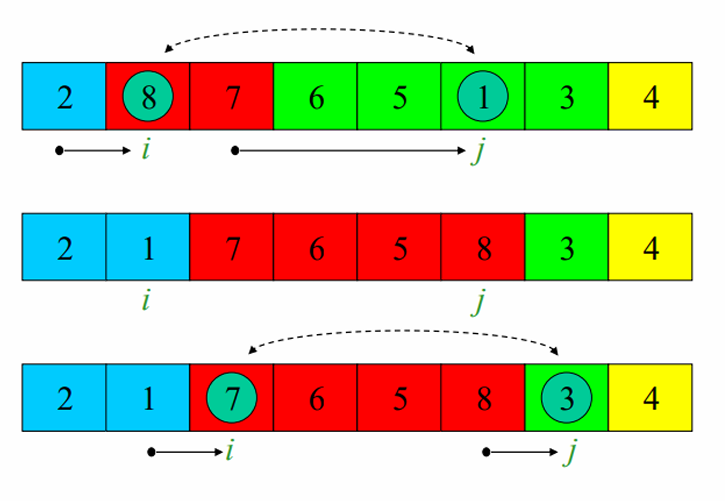
1 ≤ 4 이므로, i의 값을 하나 늘리고, A[i]와 A[j] 값을 바꿔줍니다.

위의 과정을 반복합니다.

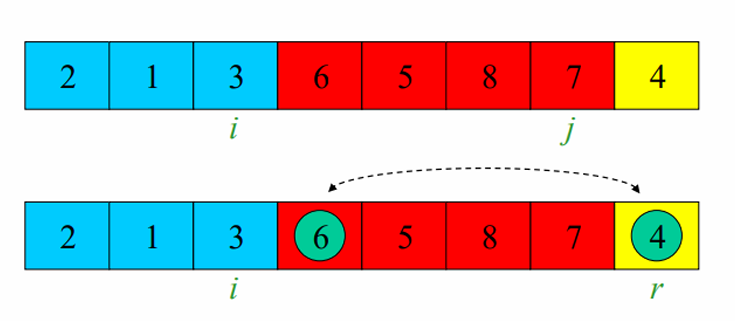
최종적으로, 피봇의 값을 원위치로 돌려줍니다.

Correctness of Partition

알고리즘이 올바르게 작동하는지 학인하기 위해 루프불변성을 이용해야합니다.

루프불변식은 다음과 같습니다.

$A[p .. i]$ 의 모든 항목은 피봇보다 작거나 같습니다.
$A[i+1 .. j-1]$ 의 모든 항목은 피봇보다 큽니다.
$A[r]$ 은 피봇입니다.

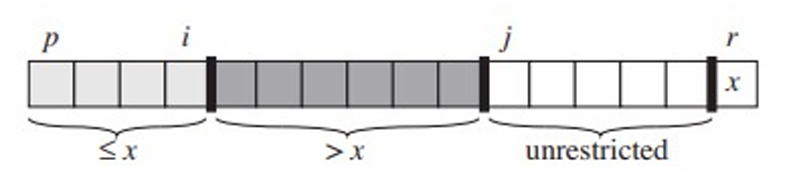
Initialization

초기화 단계에서는 루프가 시작되기 전에 불변식의 모든 조건이 만족되어야 합니다.
이 단계에서 r이 피봇이 되고, 부분 배열 A[p .. i]와 A[i+1 .. j-1]는 비어 있습니다.

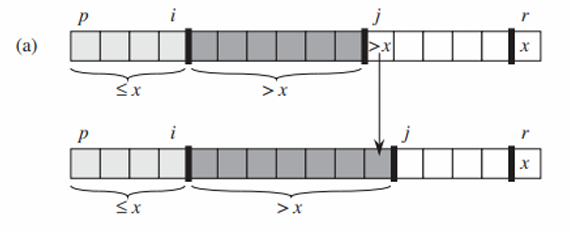
Maintenance

유지단계에서는 루프가 실행되는 동안 불변식은 다음과 같이 유지되어야 합니다.

$A[j]$ > 피봇인 경우, j만 증가합니다.
$A[j]$ <= 피봇인 경우, 인덱스 i가 증가하고, A[i]와 A[j]가 교환되며, 그 다음 j가 증가합니다.

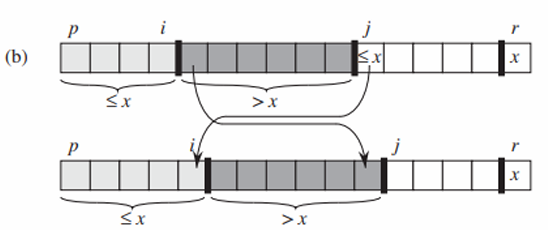
Termination

종료 단계에서는 루프가 종료될 때 불변식이 여전히 유지되어야 합니다.
j=r 이 되며, 배열 A의 모든 요소는 피봇을 기준으로 크기가 나누어진 부분배열으로 나누어집니다.
$A[p .. i] <= pivot$
$A[i+1 .. r-1] > pivot$
$A[r] = pivot$