Priority Queues
- HeapSort는 좋은 알고리즘이지만, 실제로는 우선순위 큐가 더 자주 쓰입니다.
- 힙 데이터구조는 우선순위 큐 구현에 매우 효율적입니다.
- 각 요소가 키값또는 키와 연관된 동적 집합 S를 유지하기 위한 데이터구조입니다.
- Insert(), Maximum(), ExtractMax(), changeKey() 연산을 지원합니다
Operations on Dynamic Sets
동적집합이란?
- 동적집합은 데이터요소를 저장하고 관리하는 데이터구조로, 요소의 추가, 삭제, 검색 등을 지원합니다. 동적집합은 특정연산을 지원하며, 이러한 연산들은 집합의 요소를 변경하거나, 집합에 대한 정보를 제공하는데 사용됩니다.
동적집합의 주요 연산
- INSERT(S, x): 집합 S에 요소 x를 추가합니다.
- DELETE(S, x): 집합 S에 요소 x를 제거합니다.
- SEARCH(S, k): 집합 S에서 키가 k인 요소를 검색합니다.
- 예를 들어, 현재 집합 S={(1',a'),(2',b'),(3',c')} 에서 k=2를 검색하면 결과는 (2',b')가 됩니다. - MAX(S):집합 S에서 가장 큰 값을 가진 요소를 반환합니다.
예시: 예를 들어, 현재 집합 - MIN(S):집합 S에서 가장 작은 값을 가진 요소를 반환합니다.
- EXTRACT-MAX(S): 집합 S에서 가장 큰 값을 가진 요소를 반환하고 제거합니다.
- EXTRACT-MIN(S): 집합 S에서 가장 작은 값을 가진 요소를 반환하고 제거합니다.
- SUCCESSOR(S, x): 집합 S에서 요소 x의 다음 큰 값을 가진 요소를 반환합니다.
- 예를 들어, 현재 집합 S={1,3,4,5}에서 x=3의 SUCCESSOR는 4입니다. - PREDECESSOR(S, x): 집합 S에서 요소 x의 이전 작은 값을 가진 요소를 반환합니다.
- 예를 들어, 현재 집합 S={1,3,4,5}에서 x=3의 PREDECESSOR는 1입니다.
동적 집합에서 힙의 역할
힙 데이터구조는 우선순위 큐를 구현하는데 유용합니다. 우선순위 큐는 다음과 같은 연산을 효율적으로 지원합니다.
-
Insert()
- 새로운 요소 x를 우선순위 큐에 추가합니다.
- 최대 힙 또는 최소 힙을 사용하여 O(log n) 시간에 삽입이 가능합니다.
-
Maximum() / Minimum():
- 최대 힙의 경우, 최대값을 O(1) 시간에 반환합니다.
- 최소 힙의 경우, 최소값을 O(1) 시간에 반환합니다.
-
Extract-Max() / Extract-Min():
- 최대 힙의 경우, 최대값을 반환하고 제거한 후, 힙 속성을 유지합니다.
- 최소 힙의 경우, 최소값을 반환하고 제거한 후, 힙 속성을 유지합니다.
- 두 경우 모두 시간 복잡도는 O(log n)입니다.
-
ChangeKey(x, new_key):
-요소 x의 키 값을 새로운 값 new_key의 값으로 변경합니다.
- 키값을 변경함에 따라 힙의 크기나 순서가 바뀔 수 있기때문에, 힙 속성을 유지하기 위해 재정렬이 필요할 수 있습니다.
Priority Queues의 구현
Priority Queues_Sorted linked list
정렬된 연결리스트를 사용한 우선순위 큐에 대해 알아보겠습니다.
-
Insert
- 리스트를 스캔하여 새 항복을 삽입할 위치를 찾고, 그 위치에 항목을 삽입하면 됩니다.
- 시간복잡도는 이 됩니다.
-
Extract Max
-
리스트가 정렬되어 있으므로, 가장 첫번째 원소를 가져오면 됩니다.
-
시간복잡도는 이 됩니다.
-
리스트가 정렬되어있다면, 추출할 때 시간이 적게걸리고, insert할때는 시간이 오래걸립니다.
Priority Queues_UnSorted linked list
정렬되지 않은 연결리스트를 사용한 우선순위 큐에 대해 알아보겠습니다.
-
Insert
- 새로운 요소를 리스트의 앞에 추가합니다.
- 시간복잡도는 이 됩니다.
-
Extract Max
-
리스트 전체를 탐색하여 최댓값을 찾아야 합니다.
-
시간복잡도는 이 됩니다.
-
리스트가 정렬되어있지 않다면, 추출할 때 시간이 오래걸리고, insert할때는 시간이 적게걸립니다.
많은 추출연산이 필요한 경우 정렬된 리스트가 더 나은 성능을 보이고, 삽입이 빈번한 경우 정렬되지않은 리스트가 더 유리할 수 있습니다.'
Priority Queues_Heap
-
INSERT와 EXTRACT-MAX 의 시간복잡도는 모두 으로 어느 한쪽에 치우치지 않고 양쪽 모두 좋은 성능입니다.
-
EXTRACT-MAX: 앞에서 설명한 최대힙에서 최댓값을 추출하는 방법과 동일합니다.
-
INSERT: 삽입은 Insertion-Sort와 유사합니다.
-
HEAPIFY와 비슷하게 O(log n) 노드를 트래버스하지만 HEAP-INSERT 비교와 할당이 적습니다.
왜냐하면, HEAPIFY는 부모를 두 자식과 비교하지만, HEAP-INSERT는 하나의 부모와만 비교하기 떄문입니다.
HEAP-INSERT(A, key, n)
n ← n + 1
i ← n
while i > 1 and A[⌊i/2⌋] < key do
A[i] ← A[⌊i/2⌋]
i ← ⌊i/2⌋
A[i] ← key
예를 통해 Heap-Insert 를 알아봅시다.
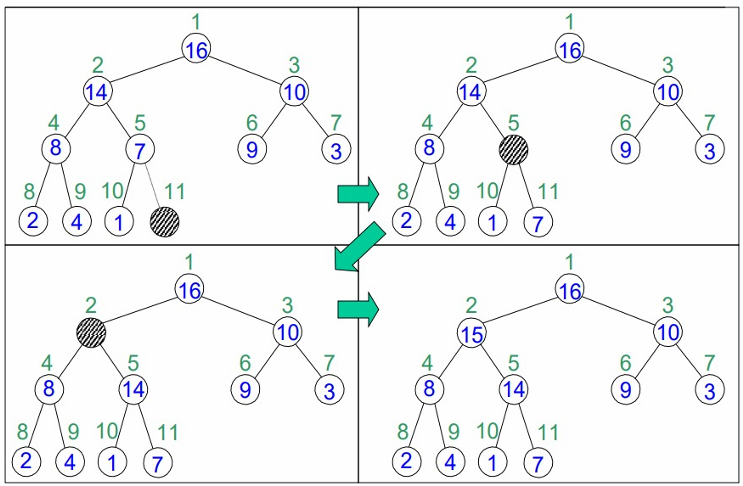
1. 새로운 요소를 배열의 끝에 추가합니다
2. 새로운 요소 '15'를 부모 노드 A[5] = 7과 비교합니다.
3. 15 > 7이므로, 15를 A[5]로 이동시킵니다.
4. 다시 15의 부모 노드 A[2] = 14와 비교합니다.
5. 15 > 14이므로, 15를 A[2]로 이동시킵니다.
6. 이제 15의 부모 노드 A[1] = 16과 비교합니다.
7. 15 < 16이므로, 15는 A[2]에 위치하게 됩니다.
Heap Increase Key
- Heap Increase Key 이란 힙의 i번째 요소의 키값을 증가시키는 것 입니다.
- 만약 새로운 키값이 기존값보다 작으면 에러를 반환합니다.
- 새로운 키 값이 부모보다 클 때까지 부모와 비교하여 교환합니다.
예시를 통해 알아봅시다
HEAP-INCREASE-KEY(A, 9, 15)
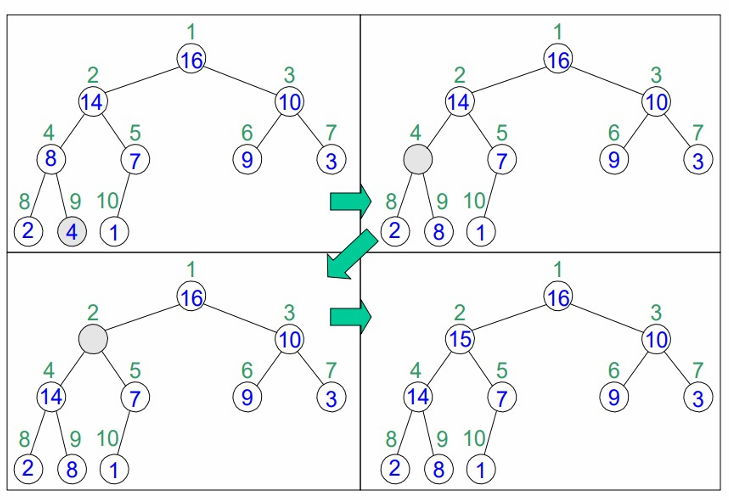
- A 배열의 9번째 요소의 키 값을 15로 증가시키는 과정입니다.
- 새로운 요소 15를 삽입하고, 힙 속성을 유지하기 위해 부모와 비교하여 올바른 위치로 이동시킵니다.
