[algorithm] 그리디 알고리즘

현굥·2024년 9월 10일

algorithm

목록 보기

11/17

Greedy algorithm

그리디 알고리즘과 동적프로그래밍

그리디 알고리즘과 동적프로그래밍

그리디 알고리즘은 동적프로그래밍의 복잡한 계산방식에 대한 대안으로 생겨났습니다. 동적 프로그래밍은 모든 부분 문제를 풀고 부분 문제의 최적해를 저장하여 중복 계산을 방지하는 방식입니다.

메모이제이션을 통해 중복된 계산을 줄이지만, 불필요하게 많은 계산을 수행할 수 있기 떄문에 비효율적일 수 있습니다.

통적프로그래밍과 같이 최적부분구조를 기반으로 하지만, 탐욕적인 선택이라는 개념을 통해 문제를 효율적으로 해결하기 위해 그리디 알고리즘이 생겼습니다.

그리디 알고리즘이란 ?

최적의 해를 구하는데 사용되는 근사적인 방법입니다. 그리디 알고리즘은 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달합니다.

그리디 알고리즘은 현재 상황에서 가장 좋은 결과를 선택해 나가지만, 최종적인 결과에 대한 최적해를 보장해주지는 않습니다.

즉, 그리디 알고리즘을 사용한다고 무조건 최적해가 나오는것은 아닙니다.

그러나 아래의 두 조건을 만족시키면, 그리디 알고리즘을 사용하면서 최적해를 도출해낼 수 있습니다.

그리디 알고리즘 조건

그리디 알고리즘을 사용하기 위한 조건은 두가지가 있습니다.

아래의 두 조건은 모든 문제에 적용되는것은 아닙니다.

앞에서 언급했듯, 각 단계에서 최적의 선택을 한다고 하여도 전체 문제에 대한 최적해가 도출되지 않을수도 있을 수 있기 때문입니다.

아래의 두 속성을 모두 만족시킬때 그리디 알고리즘을 사용하여 전체문제에 대한 최적해를 구할 수 있습니다.

1. 탐욕 선택 속성(Greedy Choice Property)

그리디 알고리즘은 문제를 해결하는 과정에서 각 단계에서 현 시점에서 가장 최적인 선택을 함으로써, 그 선택이 전체문제를 해결하는데 있어서 최적해를 보장할 수 있어야 한다는 의미입니다.

2. 최적 부분 구조(Optimal Substructure)

문제를 작은 부분문제로 나눌 수 있고, 그 부분 문제들의 최적 해가 전체 문제의 최적해로 이어질 때 이 속성이 성립합니다.

동적 프로그래밍과 탐욕알고리즘 모두 최적 부분 구조가 성립하는 문제에만 적용될 수 있습니다.

동적프로그래밍과 탐욕알고리즘은 문제를 부분문제로 나누어 해결한다는 공통점이 있지만, 어떻게 해결하는지에서 차이가 납니다.

그리디 알고리즘은 각 단계에서의 탐욕적인 선택이 이후의 선택에 영향을 주지 않고 최적해로 이어질 수 있어야 하는 문제가 중요합니다.

예를 들어 서로 다른 정수가 적혀있는 완전이진트리가 있는데, Tree의 root node 부터 시작해서 float하여 내려오며 최종적으로 가장 큰 수를 찾는 문제가 있다고 해봅시다.
이 문제에 그리디 알고리즘을 적용하게 되면, tree의 각 레벨에서 최선의 선택을 하며 두 자식노드의 크기를 비교 한 이후, 적혀있는 값의 크기가 더 큰 자식노드을 선택하게 될 것 입니다.

이때, leaf node중 하나가 말도안되게 큰 수라서 그 값의 방향으로 자식을 선택하는 일은 있어서는 안됩니다.
즉, 값들이 이전 단계의 선택에 영향을 주어서는 안됩니다.

알고리즘 예시

동적 프로그래밍을 사용하는 대표적인 문제로는 0-1 Knapsack Problem 과 같은 문제가 있습니다.
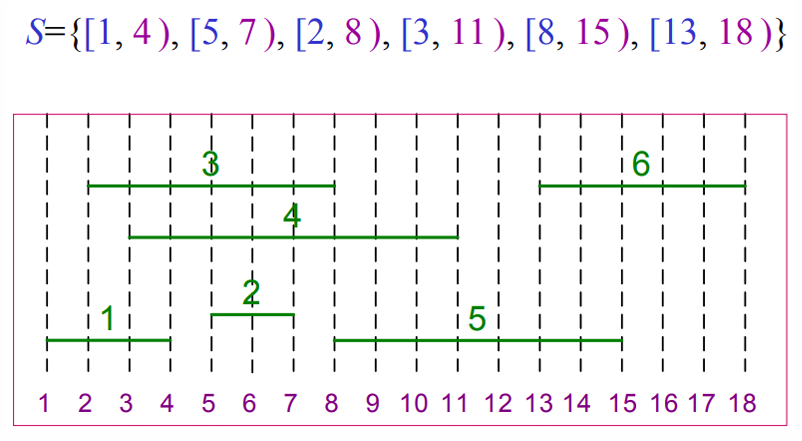
동적 프로그래밍과 그리디알고리즘 모두 사용할 수 있는 대표 문제로는 Activity selection Problem 같은 문제가 있습니다.

1. 0-1 Knapsack Problem_ DP

이 문제는 특정한 용량이 주어지고, 용량은 배낭에 넣을 수 있는 물건의 최대무게를 의미합니다.

물건은 무게와 가치로 주어집니다.

목표는 주어진 물건들을 배낭에 넣어 최대 가치를 얻도록 선택합니다. 이때 배낭에 들어가는 물건들의 총 무게는 배낭의 용량 𝑊를 초과할 수 없습니다.

이 문제는 탐욕 알고리즘으로는 일반적으로 최적해를 보장할 수 없고 동적 프로그래밍을 사용하여 해결하는 것이 적합합니다.

2. Activity selection Problem_ DP, Greedy

이 문제는 n개의 활동이 있을 때, 활동할 수 있는 최대 활동 수를 찾는 문제입니다.
이 문제는 최적부분구조로 나누어 해결할 수 있기 떄문에, 동적프로그래밍 관점에서도 볼 수 있고, 탐욕알고리즘 관점에서도 볼 수 있습니다.

$S={1,2,...,n}$ 는 $n$ 개의 활동을 나타냅니다.
$S_𝑖$ : 활동 $i$ 의 시작 시간
$𝑓_𝑖$ : 활동 𝑖의 종료 시간

두 활동을 동시에 하려면, $[ S_𝑖,𝑓_𝑖 )$ 와 $[ S_j,𝑓_j )$ 는 겹치면 안됩니다.

문제 해결

위의 문제를 해결하기 위해 최적의 부분구조를 결정해야합니다.
이후, 재귀적인 해결책을 개발해야합니다.
각 단계에서 탐욕적인 선택을 했을떄, 하나의 부분문제만 남는다는것을 보여줘야 합니다. 그리고, 각 선택은 항상 안전하다는것을 증명해야 합니다.
마지막으로 이를 반복적인 알고리즘으로 변환해야 합니다.

$S_{ij}$ 는 $a_i$ 가 끝난 후 시작하고 $a_j$ 가 시작되기 전에 끝나는 활동을 나타냅니다.

동적프로그래밍을 사용했을 경우와 탐욕알고리즘을 이용하는 두가지 관점에서 살펴봅시다.

Optimal Substructure_ DP

$A_{ij}$ 는 $S_{ij}$ 내에서 호환 가능한 활동들의 최대 크기 집합입니다.
- $A_{ij}$ 는 활동 $a_i$ 가 끝난 후, $a_j$ 가 시작되기 전에 실행할 수 있는 최대 크기의 호환 가능한 활동 집합입니다.
- 즉, $S_{ij}$ 에서 가능한 최적해를 구하는 집합이 $A_{ij}$ 입니다.
$a_k$ 를 $A_{ij}$ 의 한 활동으로 선택합니다.
- $a_k$ 를 선택하게 되면, $a_k$ 를 기준으로 아래와 같은 두 개의 작은 부분 문제로 나놀 수 있습니다.

첫 번째 부분 문제: $S_{ik}$ 에서 호환 가능한 활동을 찾습니다.
- $S_{ik}$ 는 $a_i$ 가 끝난 후 시작하고, $a_k$ 가 시작되기 전에 끝나는 활동들로 구성된 부분 문제입니다.
- 즉, 활동 $a_k$ 가 시작되기 전까지 호환 가능한 활동들을 찾아야 합니다.
두 번째 부분 문제: $S_{kj}$ 에서 호환 가능한 활동을 찾습니다.
- $S_{kj}$ 는 $a_k$ 가 끝난 후 시작하고, $a_j$ 가 시작되기 전에 끝나는 활동들로 구성된 부분 문제입니다.
- 즉, 활동 $a_k$ 가 끝난 이후부터 $a_j$ 가 시작되기 전까지 호환 가능한 활동들을 찾아야 합니다.
위의 내용을 정리하자면 아래와 같습니다.

Optimal Substructure

$A_{ik}$ : $a_i$ 와 $a_k$ 사이에서 호환 가능한 최대 크기의 활동 집합.
$A_{kj}$ : $a_k$ 와 $a_j$ 사이에서 호환 가능한 최대 크기의 활동 집합.

$A_{ij}$ 는 $A_{ik} \cup \{a_k\} \cup A_{kj}$ 을 의미합니다.

즉, $A_{ij}$ 는 $a_i$ 와 $a_j$ 사이에서 $a_k$ 를 선택하고, 그 사이에서 호환 가능한 최대 크기의 활동 집합을 찾는 문제로 나눌 수 있습니다.
최종적으로 $A_{ij}$ 의 크기는 아래와 같습니다

|A_{ij}| = |A_{ik}| + |A_{kj}| + 1

이때, 1은 $a_k$ 를 선택한 경우를 나타냅니다.

정리하자면, 활동 선택 문제는 최적 부분 구조를 가지고 있으며 이를 통해 문제를 작은 부분문제로 나누고 해결할 수 있습니다.
이후, $A_{ij}$ 의 최적해는 $a_k$ 를 기준으로 두 개의 부분 문제로 나누어 각각 해결한 후 결합하여 최종 최적해를 구하는 방식입니다.

Claim

최적해 $A_{ij}$ 는 두 부분 문제 $S_{ik}$ 와 $S_{kj}$ 에 대한 최적해를 포함해야 합니다.

Proof

cut-and-paste 논증을 사용합니다. 여기서는 $S_{kj}$ 에 대해 알아보겠습니다. 반대의 경우도 같은 방법으로 하면 됩니다.

만약 $S_{kj}$ 에서 호환 가능한 활동들의 집합 $A_{kj}'$ 가 존재하고, 그 크기 $|A_{kj}'| > |A_{kj}|$ 인 경우, 이 집합 $A_{kj}$ 대신에 $A_{kj}'$ 를 사용하여 $S_{ij}$ 부분 문제를 해결할 수 있습니다.

그렇게 되면, 새로 만들어진 호환 가능한 활동들의 집합의 크기는 다음과 같습니다.

|A_{ik}| + |A_{kj}'| + 1 > |A_{ik}| + |A_{kj}| + 1 = |A|

기존의 최적해인 $A_{kj}$ 보다는 더 큰 활동집합이 생기게 되므로, 기존에 $A_{kj}$ 가 최적해라는 가정과 모순됩니다.

따라서, $A_{ij}$ 는 최적해입니다.

이제, $A_{ij}$ 가 최적해라는걸 증명했습니다. 결과를 이용해서, 최적 부분 구조를 만족하는지 증명해봅시다.

최적해 $A_{ij}$ 이므로, 부분 문제 $S_{ik}$ 와 $S_{kj}$ 에 대한 최적해를 포함해야 합니다.

$c[i, j]$ : $S_{ij}$ 에서 최적해의 크기를 나타내고 다음을 만족합니다.

c[i, j] = c[i, k] + c[k, j] + 1

어떤 활동 $a_k$ 를 선택해야 할지 모르므로, 동적프로그래밍을 이용하면 모든 활동 $a_k$ 에 대해 시도하여 가장 큰 값을 구해야 합니다.
이를 수식화하면 아래와 같이 나타낼 수 있습니다.

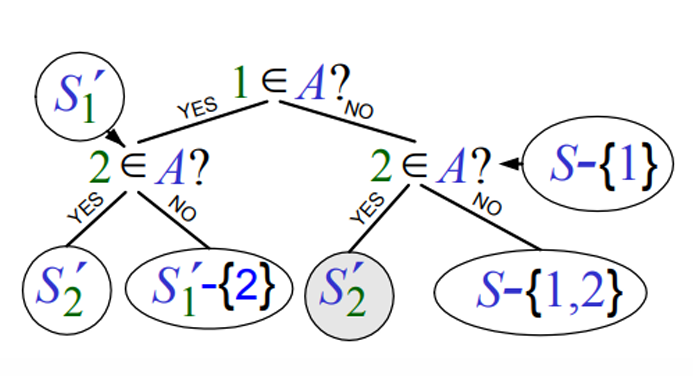
c[i, j] = \begin{cases} 0 & \text{if } S_{ij} = \emptyset \\ \max_{a_k \in S_{ij}} \{c[i, k] + c[k, j] + 1\} & \text{if } S_{ij} \neq \emptyset \end{cases}

위의 과정을 트리로 표현한다면 아래와 같습니다.

이때, 정수는 활동, A는 최적해를 구성하는 집합, S는 전사건으로 보고, S'은 S의 부분집합으로 이해하면 됩니다.

예를 들어, S - {1, 2}은 활동 1과 2를 선택한 후 남은 활동들의 집합을 나타내고, S'1는 활동 1을 포함하고 나머지 활동들에 대해 최적해를 찾는 부분 문제입니다.

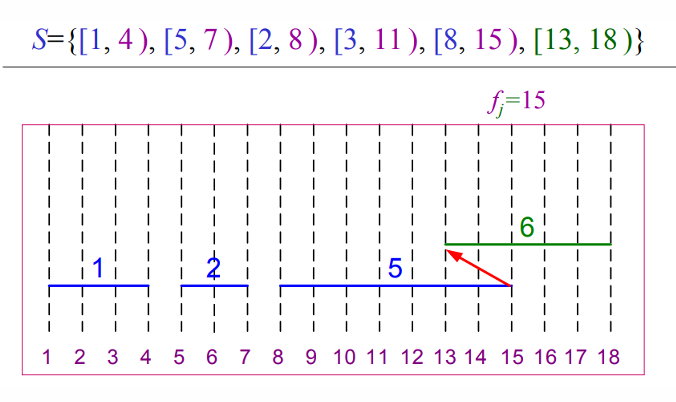
Activity Selection Problem _Greedy

Activity Selection Problem에서는 반복되는 부분 문제와 최적 부분 구조가 성립합니다.
앞에서는 동적프로그래밍 관점에서 증명하였지만, 각 단계에서 탐욕적 선택을 하면 전체 최적해를 얻을 수 있습니다.

앞의 방법과 동일하게, 활동들의 종료 시간을 다음과 같이 가정합니다.
$f_1 \leq f_2 \leq \dots \leq f_n$

Greedy choice

정리(Theorem)
최적해 $A \subseteq S$ 는 활동 1을 포함하는 답입니다.
( $f_1 \leq f_2 \leq \dots \leq f_n$ 가정)

Proof:

$A = \{k, \ell, m, \dots\}$ 을 최적해로 가정하고, $f_k \leq f_\ell \leq f_m \leq \dots$ 이라고 하자.

만약 $k = 1$ 이라면, 최적해 $A$ 는 활동 1을 포함합니다.

만약 $k > 1$ 이라면, 활동 1을 포함하는 또 다른 최적해가 존재함을 보일 수 있습니다.

$B = A - \{k\} \cup \{1\}$ 로 두면, 활동 1은 $A - \{k\}$ 와 호환되므로, $B$ 도 최적해가 됩니다.
$|B| = |A| - 1 + 1 = |A|$ 이므로, $B$ 도 최적해입니다.

따라서, 최적해 $A$ 는 활동 1을 포함하며, 이는 탐욕적인 선택이 최적해를 보장함을 의미합니다.

Greedy algorithm

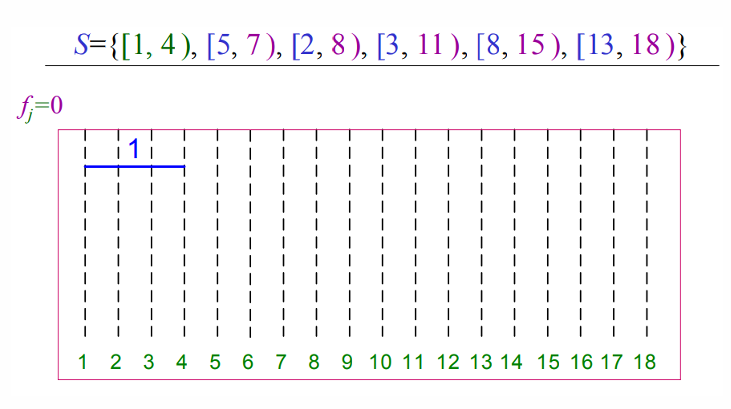
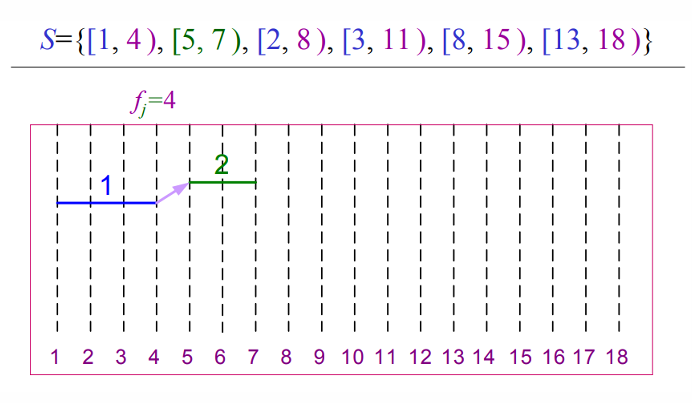
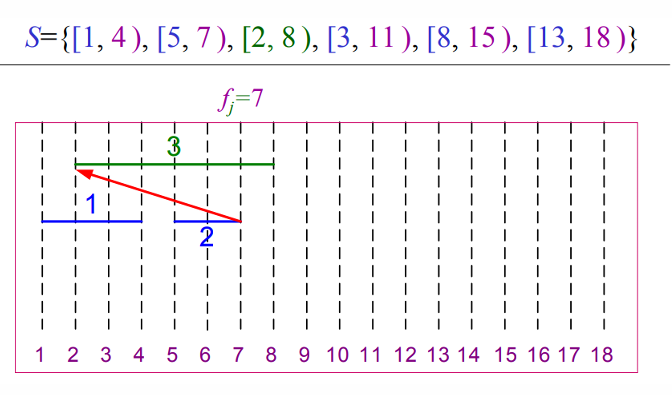
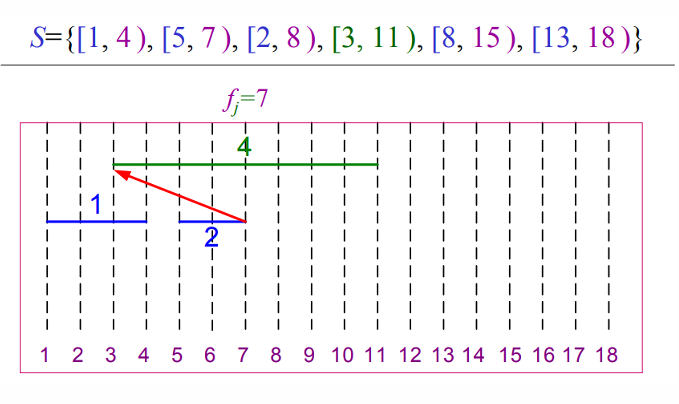
def REC_ACTIVITY_SELECTOR(s, f, k, n):
    m = k + 1
    while m <= n and s[m] < f[k]:
        m = m + 1
    if m <= n:
        return {a[m]} | REC_ACTIVITY_SELECTOR(s, f, m, n)
    else:
        return ∅

# 초기 호출
REC_ACTIVITY_SELECTOR(s, f, 0, n)