[algorithm] 분할 정복 기법

이진탐색 (Binary search)

---

1. Divide: 정렬된 배열의 중간값을 확인합니다.
2. Conquer: key값을 Arr[mid]값과 비교합니다.
   만약 일치하면 탐색이 완료됩니다. 목표 값이 작다면 왼쪽 하위 배열을, 크다면 오른쪽 하위 배열을 재귀적으로 탐색합니다.

이진탐색의 재귀적 정의

• 이진탐색은 배열을 반으로 나누고, 하나의 subArray만을 탐색하기 때문에, 다음의 재귀방정식으로 나타낼 수 있습니다.

  $T(n) = T(n/2) + Θ(1)$

  의미는 다음과 같습니다.

• $T(n/2)$ 의 계수: subproblem의 갯수

• $n/2$ : subproblem의 size

• $Θ(1)$ : divide한 problem들을 합칠때 드는 연산

• 여기서 n은 문제의 크기를 나타내고, $Θ(1)$ 은 중간 요소를 확인하는 시간입니다.

이진탐색의 시간복잡도

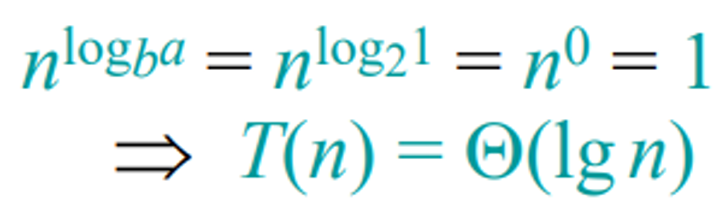
• 재귀방정식을 통해 이진 탐색의 시간 복잡도가 Θ(log n)임을 알 수 있습니다.

Recursive Binary Search 의 Pesudo code

BinarySearch (A[1..N], value)  
if (N == 0) 
return -1;
 mid = (1+N)/2;
 if (A[mid] == value) 
return mid;
 else if (A[mid] > value) 
// not found
 // found 
return BinarySearch (A[1..mid-1], value); 
else 
return BinarySearch (A[mid+1, N], value)

---

거듭제곱

---

거듭제곱 또한 분할정복 알고리즘을 적용할 수 있습니다.
예를 들어 $a^n$을 계산한다고 해봅시다

거듭제곱 _ 기본 계산 방법

• 일반적으로 $a^n$을 만들려면 a를 n번 곱해야하므로, 총 n번의 연산횟수가 필요합니다. 이 경우, Θ(n)의 시간복잡도를 가집니다.
• 거듭제곱을 구할때 분할정복을 이용한다면, running time을 계산할 수 있습니다.

거듭 제곱_ 분할 정복 알고리즘

• n이 짝수일 때와 홀수일 때의 경우를 나누어 a^(n/2) 또는 a^(n/2) * a의 형식으로 문제를 나눕니다.
• 매 단계마다 n을 절반으로 줄이기 떄문에 연산횟수는 log2 n 단계만큼 필요합니다. 따라서, 시간 복잡도는 Θ(log n)으로 개선됩니다.

---

피보나치 수열(Fibonacci numbers)

---

• 피보나치 수열을 분할정복 기법을 이용해 계산하는 방법에는 여러가지가 있지만, 대표적으로 단순 재귀 방법과 행렬거듭제곱 방법이 있습니다.

Fibonacci numbers_ recursive

• 첫 번째 항은 0, 두 번째 항은 1이며, 그 이후의 모든 항은 앞의 두 항의 합으로 이루어집니다.
• 위의 식은 Naive한 방법으로 각 재귀호출마다 두개의 추가적인 재귀호출이 발생하게 됩니다. 따라서, 함수호출의 수가 지수적으로 증가하게 되고, 이를 황금비율을 포함한 표현식으로 근사한다면, 피보나치 수열 자체가
  𝜙의 거듭제곱과 비슷하게 증가하기 때문에 n번째 피보나치 수
  $F_𝑛$ 은 약 $\Theta$(𝜙$^𝑛$)에 비례합니다.

• 황금비율이 이해하기가 어렵다면, 함수를 한번 호출할 때, 두개의 함수를 호출하게 되므로, 2의 지수승으로 연산이 늘어나는 것을 확인할 수 있습니다. $O(2^n)$ 이라고 말 할 수 있습니다.

Fibonacci numbers _ 행렬 거듭제곱

보다 효율적인 분할정복 기법은 행렬 거듭제곱을 사용하는 방법입니다. 이 방법은 다음과 같은 행렬을 사용합니다:

이 행렬을 거듭 제곱하여 $n$번째 피보나치 수를 빠르게 계산할 수 있습니다. 이 때, 거듭제곱을 계산하는 데 필요한 시간 복잡도는 $O(log n)$입니다. 이를 위해 다음과 같은 방법을 사용합니다:

• 짝수 거듭제곱: $M^{2k} = (M^k)^2$
• 홀수 거듭제곱: $M^{2k+1} = M \cdot (M^k)^2$
  이 방법을 사용하면 각 재귀단계에서 문제의 크기가 반으로 줄어들므로,분할정복의 특징을 충실히 반영하면서도 효율적으로 피보나치 수를 계산할 수 있습니다.

---

행렬 곱

---

• 행렬곱에도 분할 정복 기법을 적용할 수 있습니다. 행렬을 부분행렬로 나누어 곱하는 방법과 이를 변형하여 만들어진 Strassen’s method 의 방법이 존재합니다.
• 우선 기본 행렬 곱셈방법부터 알아봅시다.

행렬 곱_ 기본 행렬 곱셈

• 행렬 곱셈은 두 행렬을 곱할 때, 다음과 같은 규칙을 따릅니다:

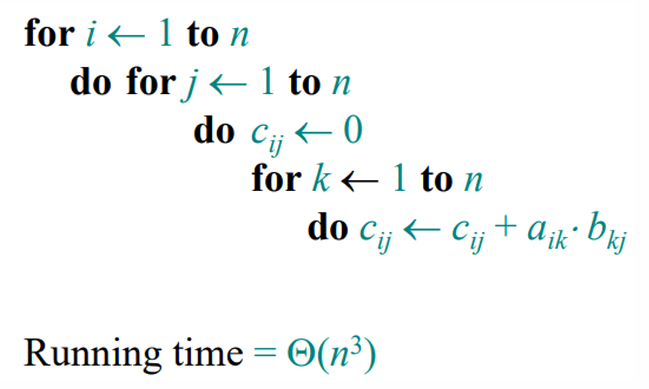
이러한 기본 행렬 곱셈 알고리즘은 3중 반복문을 사용하여 구현되며, 시간 복잡도는
𝑂(𝑛^3) 입니다.

---

행렬 곱_ 분할 정복 기법

• 분할 정복 기법은 문제를 더 작은 부분 문제로 나누어 해결하고, 그 결과를 합치는 방식입니다.
• 크기가 $n×n$ 인 두 행렬 $A, B$ 가 있다고 해봅시다.
• 크기가 $n×n$ 인 두 행렬 $A, B$를 $n/2×n/2$ 크기의 4개 하위 행렬로 나눌 수 있습니다. 이를 통해 큰 행렬 곱셈을 더 작은 행렬 곱셈으로 나누어 수행할 수 있습니다.
  $A=\begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\\ \end{pmatrix}$
  $B=\begin{pmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\\ \end{pmatrix}$

그렇게되면, 총 8번의 곱셈연산과 4번의 덧셈연산이 이루어지는 것 을 아래와 같이 확인할 수 있습니다.

따라서,

• $T_n$은 전체 문제를 해결하는 데 걸리는 시간

• $\Theta(1)$ 은 단순 스칼라 곱셈의 시간 복잡도

• $8T(n/2)$은 하위 문제 8개를 재귀적으로 해결하는 데 걸리는 시간

• $\Theta(n^2)$은 하위문제의 결과를 결합하는 데 걸리는 시간

• 이 재귀 관계식은 마스터 정리를 사용한다면 전체 알고리즘의 시간복잡도는 $\Theta(n^3)$으로 귀결됩니다. 이는 행렬 곱셈의 표준 알고리즘의 시간 복잡도와 동일합니다.

---

행렬 곱_ Strassen’s method

분할정복기법을 적용한 행렬곱 연산을 더 효율적으로 수행할 수 있는 Strassen’s method 가 있습니다. 이는, 행렬곱셈에 기존 분할 정복 기법을 적용해서 얻은 8번의 곱셈을 7번의 곱셈으로 줄일 수 있도록 설계한 방법입니다. 각 단계별로 설명하겠습니다.

1. 입력분할(Partitioning)

$n×n$ 인 두 행렬 $A, B$를 $n/2×n/2$ 크기의 4개 하위 행렬로 나눌 수 있습니다. 이를 통해 큰 행렬 곱셈을 더 작은 행렬 곱셈으로 나누어 수행할 수 있습니다.

2. 10개의 중간 행렬 생성

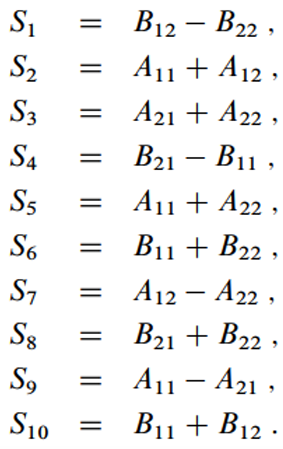
3. 7개의 곱셈수행

• Strassen의 알고리즘의 핵심은 곱셈 연산의 수를 줄이는 것입니다. 7개의 곱셈 $p_i$를 사용하여 필요한 곱셈 연산을 줄입니다.
  
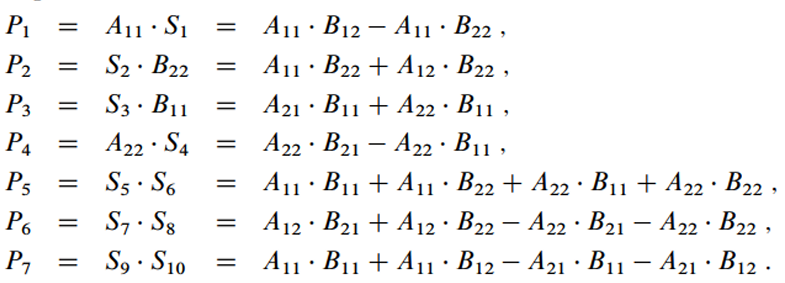
  이를 알파벳으로 치환한다면 아래와 같습니다. 총 7번의 곱셈과 18번의 덧셈/뺄셈 연산으로 이루어진것을 확인할 수 있습니다.

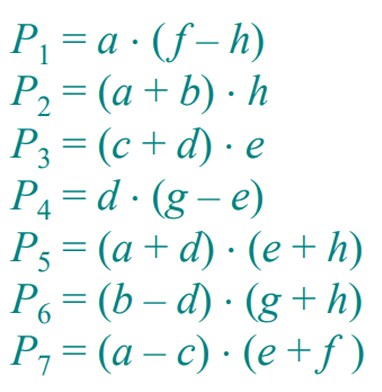
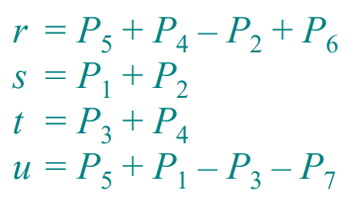
4. 결과 조합

• 마지막으로, 7개의 곱셈 결과를 이용해 최종 결과 행렬 𝐶의 부분 행렬들을 계산합니다. 이는 다시 덧셈과 뺄셈 연산으로 이루어집니다.
  
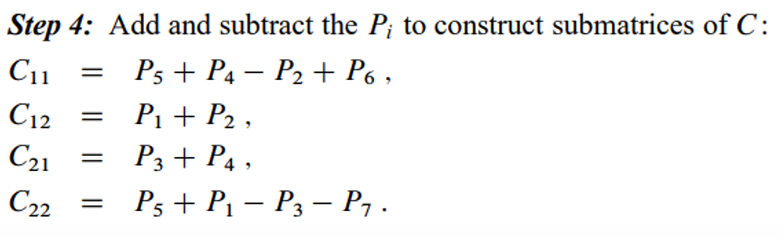
  위의 계산과정은 아래와 같습니다.
  

---

Strassen’s method의 시간복잡도 분석

• $7T(n/2)$은 하위 문제 7개를 재귀적으로 해결하는 데 걸리는 시간

• $\Theta(n^2)$은 하위문제의 결과를 결합하는 데 걸리는 시간

• 이 재귀 관계식은 마스터 정리를 사용한다면 전체 알고리즘의 시간복잡도는 $\Theta(n^{log_2^7})$≈$\Theta(n^{2.81})$ 으로 수렴합니다. 따라서, 이는 이전의 행렬곱 시간복잡도보다 효율적이라고 할 수 있습니다.