HeapSort

---

• 힙(Heap)은 자료 구조 관점에서 완전 이진 트리(Complete Binary Tree) 구조를 가진 특수한 트리 형태입니다.

• 힙 정렬은 최악의 경우에도 O(n log n)의 시간 복잡도를 가지며, 이는 매우 효율적인 정렬 방법 중 하나입니다.

• 힙 정렬은 추가 메모리를 필요로 하지 않는 제자리(in-place) 정렬 알고리즘입니다

• 힙 자료구조는 우선순위 큐 와 같은 구조에서 중요한 역할을 합니다.

• 힙은 일반적으로 다음 두 가지 종류로 분류됩니다: 최대 힙(Max-Heap)과 최소 힙(Min-Heap).

---

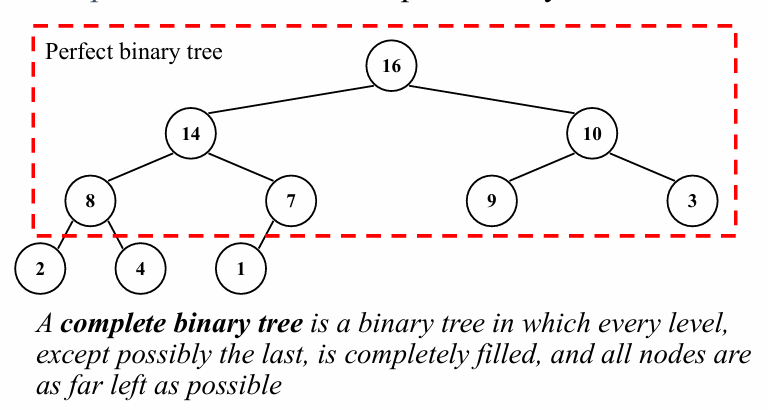
완전 이진 트리 (Complete Binary Tree)

• 완전 이진 트리는 트리의 모든 레벨이 가득 차 있거나 마지막 레벨이 왼쪽부터 순서대로 채워진 구조를 의미합니다.
  

Heap Data Structure

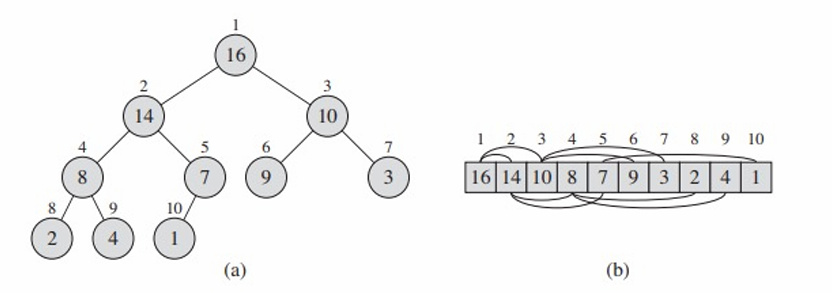
• 실제 힙은 배열을 통해 구현되며, 이를 통해 효율적인 메모리 사용이 가능합니다. 배열 인덱스를 이용해 부모와 자식노드간의 관계를 쉽게 관리할 수 있습니다.
• 루트 노드의 위치: $A[1]$
• 노드 $i$의 부모: $A[⌊𝑖2⌋]$
• 왼쪽 자식의 위치: $A[2i]$, 오른쪽 자식의 위치: $A[2i + 1]$
  

Heap Data Structure 2

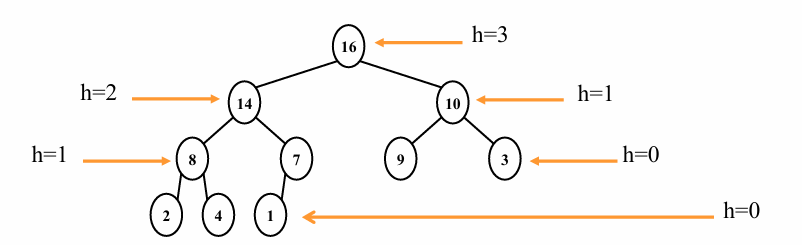
• The height of a node = 루트에서 해당 노드까지의 경로의 최대 길이
• The height of a tree = the height of its root
• The depth of a node = 루트에서 해당 노드까지의 경로 길이
• The height of an n-element heap : $⌊log_2(𝑛)⌋$
• 이때, 힙 연산의 시간 복잡도는 힙의 높이에 비례합니다.

---

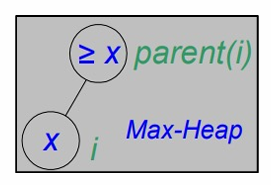
Heap Property(MAX)

• 힙은 모든 노드 i에 대해 $A[parent(i)] ≥ A[i]$ 조건을 만족합니다.

• 즉, 모든 노드 i에 대해 부모 노드의 값이 자식 노드의 값보다 크거나 같아야 합니다.

• 사진처럼, 서브트리에서 가장 큰 요소는 항상 그 서브트리의 루트에 위치합니다

• 최대 힙은 우선순위 큐(Priority Queue)에서 높은 우선순위를 가지는 요소를 빠르게 꺼내기 위해 사용됩니다.

---

Heap Property(MIN)

최소힙은 최대힙과 정 반대라고 생각하면 됩니다.

• 힙은 모든 노드 i에 대해 $A[parent(i)] ≤ A[i]$ 조건을 만족합니다.
• 즉, 모든 노드 i에 대해 부모 노드의 값이 자식 노드의 값보다 작거나 같아야 합니다.
• 서브트리에서 가장 작은 요소는 항상 그 서브트리의 루트에 위치합니다
• 최대 힙은 낮은 우선순위를 가지는 요소를 빠르게 꺼내기 위해 사용됩니다.

---

Heap Operations

---

Extract Max

• 최대힙에서 최대값, 즉, root를 추출하는 과정에 대해 알아보겠습니다.
  
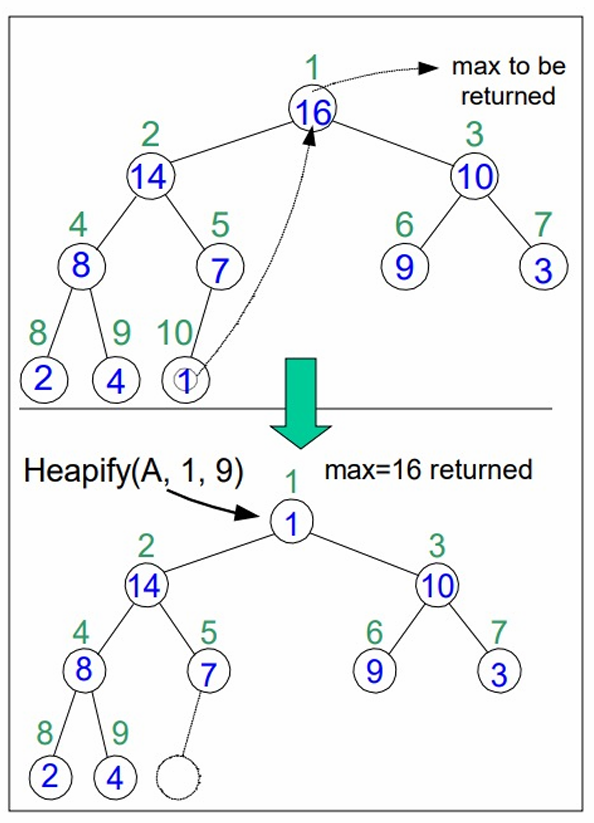
• 최대값(16)을 A[1]에서 가져오고, 마지막 노드 A[10]을 루트 노드 위치로 이동시킵니다.
• 노드 수를 10에서 9로 줄이고, 루트 노드에서 힙 속성을 복원하기 위해 HEAPIFY(A,1,9) 과정을 수행합니다.

---

Extract Max_ Pesudo Code

• Extract Max의 의사코드는 다음과 같습니다.

• 최대값을 A[1]에서 가져오고, 마지막 노드 A[n]을 루트 노드 위치로 이동시킵니다.
• 노드 수 n을 1 줄이고, 루트 노드에서 힙 속성을 복원하기 위해 HEAPIFY 과정을 수행합니다.
• 이 과정의 시간 복잡도는 O(1) + 힙 속성 복원 시간입니다.

---

HEAPIFY

• HEAPIFY란 노드 $i$에서 시작하여, 자식 노드와 비교하면서 힙 속성을 유지하도록 값들을 조정하는 과정입니다.
• 왼쪽 자식 노드 $left[i]$와 오른쪽 자식 노드 $right[i]$가 이미 힙 속성을 만족하는 경우, 부모 노드 $A[i]$가 자식 노드들보다 작을 수 있습니다.
• $A[i]$의 값을 힙 속성을 만족하는 위치로 떠내려보내야 합니다. 이를 통해 $i$를 루트로 하는 서브트리가 힙 속성을 유지하도록 합니다.
• 아래의 그림을 통해 설명해보겠습니다.

• $2^{th} node$를 보면 값이 4이지만 $2^{th} node$의 왼쪽자식의 값은 14로 max heap의 속성을 위배하는것을 확인할 수 있습니다.
  이 경우 HEAPIFY를 수행하여 $2^{th} node$과 왼쪽자식과의 위치를 바꿉니다.
• 이후, 우측 상단의 그림처럼 $4^{th} node$ 에 4의 값이 복사된것을 확인할 수 있습니다.
• $4^{th} node$ 를 root으로 하는 서브트리 또한 max heap의 성질을 만족하여야 하므로, $4^{th} node$에 대해 HEAPIFY를 수행합니다.
• 그 결과 마지막 우측하단의 그림처럼, $4^{th} node$와 $9^{th} node$의 값을 서로 바꿔 모든 노드 $i$ 에 대해 heap의 속성을 만족하는것을 확인할 수 있습니다.

---

HEAPIFY_ Pesudo Code

• 다음은 재귀적 HEAPIFY의 의사코드입니다.

• 조건 1: $2i ≤ n$ (왼쪽 자식이 존재) 이고 $A[2i] > A[i]$(왼쪽 자식이 부모보다 큼)일 경우, $largest$를 왼쪽 자식의 인덱스인 $2i$ 로 설정합니다. 그렇지 않으면 $largest$를 $i$로 유지합니다.
• 조건 2: $2i + 1 ≤ n$ (오른쪽 자식이 존재) 및 $A[2i + 1] > A[largest]$ (오른쪽 자식이 현재 largest보다 큼)일 경우, largest를 오른쪽 자식의 인덱스인 $2i + 1$로 설정합니다.
• 교환 및 재귀 호출: $largest$가 $i$와 다를 경우, $A[i]$ 와 $A[largest]$ 를 교환한 후, HEAPIFY를 $largest$ 에서 재귀적으로 호출하여 힙 속성을 유지합니다.

---

Heapify 함수의 분석

• $HEAPIFY(A, i, n)$의 시간 복잡도를 분석해봅시다.
• $h(i)$를 노드 $i$ 의 높이라고 하면, HEAPIFY 함수는 각각의 노드에서 최대 $h(i)$ 번 재귀 호출될 수 있습니다.
• 각 노드에서는 두 노드를 교환하는 $\theta(1)$ 의 작업을 수행합니다.
• 따라서, 각 단계에서의 작업을 전체 높이에 적용하면
  $T(i)$=$O(h(i))$가 됩니다.
• 힙은 거의 완전한 이진 트리이므로, $h(i)$는 $O(log n)$이므로 HEAPIFY의 시간 복잡도는 $O(log n)$ 입니다.

---

HEAPIFY 함수의 시간 복잡도 분석

1. 재귀적 호출

• HEAPIFY 함수는 노드 $i$ 에서 호출될 때, 노드 $i$의 자식 노드가 있는 서브트리 $S_L(i)$와 $S_R(i)$를 가지고 있습니다.
• 이 서브트리들은 각각 $h(i) - 1$과 $h(i) - 2$의 높이를 가지는 완전한 이진 트리입니다.
• HEAPIFY 함수가 호출될 때마다 최대 $O(1)$의 상수 시간이 걸리며, 이는 자식 노드들과의 비교 및 필요한 교환 작업을 포함합니다.
  

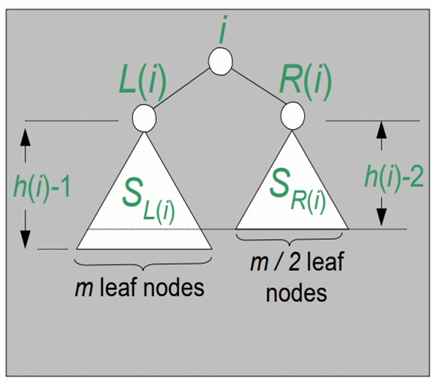
2. 노드의 수와 시간 복잡도

• $S_L(i)$의 리프 노드 수는 $|S_L(i)| = m + (m - 1) = 2m - 1$입니다.
• $S_R(i)$의 리프 노드 수는 $|S_R(i)| = m/2 + (m/2 - 1) = m - 1$입니다.
• 전체 노드 수 $n$은 $|S_L(i)| + |S_R(i)| + 1 = n$이며, 이를 통해 $m = (n+1)/3$을 얻을 수 있습니다.
• 따라서, $T(n) ≤ T(2n/3) + Θ(1)$이며, $HEAPIFY$의 시간 복잡도는 $O(log n)$입니다.

HEAPIFY_ iterations

• HEAPIFY를 재귀적으로 수행할 때는 각 재귀 호출 수준에서 스택을 사용하여 push/pop 작업이 발생합니다.
• 꼬리 재귀가 없는 경우, iterations을 이용한 구현이 더 효율적일 수 있습니다.