4. 연결리스트 (Linked List)

본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1

연결리스트

• 한방향 vs 양방향

• 배열과의 비교

  • 연속된 공간의 메모리 차지, 상수 시간의 값을 읽고 쓴다 (e.g. A[i])
  • 반면, 연결리스트는 연속된 공간이 아닌 각 메모리가 흩어져 있음
  • 현재 값의 다음 값을 알기 위해, 현재 값과 다음 값의 주소를 한꺼번에 저장해야 됨
  • 즉, 2개의 값 필요 ➡️ data 값(key), link(다음 값의 주소) ➡️ (key, link)의 쌍 = Node
    

• 연결리스트: 각각의 Node로 연결된 리스트

  • 단점: 상수 시간에 값을 읽고 쓰지 못함. 맨 앞의 노드인 head node를 타고 link를 따라가서 원하는 위치의 값을 읽음 (찾고자하는 위치까지의 시간이 더 필요)
  • 장점: 새로운 노드(c)를 중간에 삽입하고자 할 때, 이전의 노드(a)와 다음 노드(b)의 링크를 바꾸어 연결시켜주기만 하면 됨 (a-c-b)
    • insert: $O(1)$ 시간 (단 a,b를 알고있다는 가정 하에)
    • 배열에서는 중간 위치에 새로운 값을 삽입하고자 할 때, 오른쪽 값들을 한 칸씩 이동하여 그 공간을 비워줘야 함 (최악의 경우 $O(N)$의 시간)

한방향 연결리스트 vs 양방향 연결리스트

• 한방향 연결리스트: 한쪽 방향으로만 링크 존재
  • key값과 link 각각 1개 갖고 있음

• 양항뱡 연결리스트: 양쪽 방향으로 링크 존재
  • key 값과 2개의 link를 갖고 있음

1. 한방향 연결리스트 (Singly Linked List)

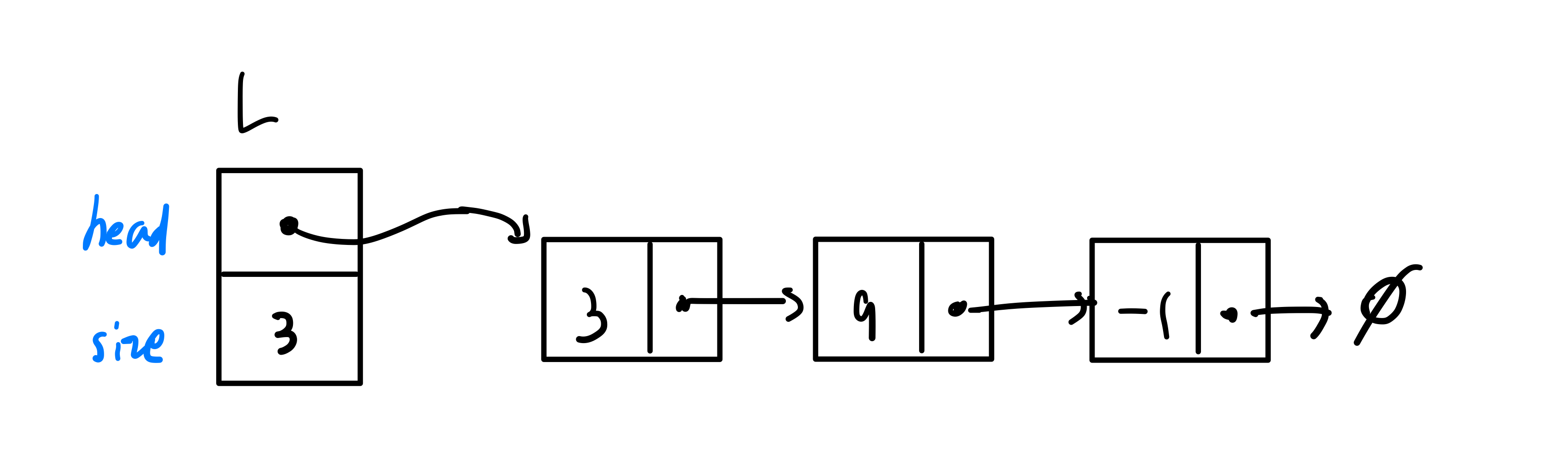
노드 클래스 정의

class Node:
	def __init__(self, key=None):
    	self.key = key
        self.next = None # link, default가 None
     
    def __str__(self):
    	return str(self.key) 

• __str__: print(v)처럼 노드 자체를 출력 ➡️ 알아서 key 값을 출력
  • = print(v.__str__())
  • 원래 key 값 출력: print(v.key)

a = Node(3)
b = Node(9)
c = Node(-1)
a.next = b
b.next = c

• 각 노드마다 변수를 할당해야 하는 번거로움 ➡️ 가장 앞 노드 Head Node만 정의해줌

  • 그 뒤 노드는 Head Node만 따라가면 되니깐
  • 맨 마지막 노드는 Tail Node

1-1. 삽입 연산: pushFront, pushBack

• PushFront: 현재 리스트의 head node 앞에 새로운 노드 삽입
• PushBack: tail node 다음에 새로운 노드 삽입

# head Node와 linked list의 개수를 저장해놓은 size 또다른 class 정의
# 한방향 연결리스트의 객체

class SinglyLinkedList:
	def __init__(self):
    	self.head = None # 처음에는 빈 리스트
        self.size = 0 # 처음에는 비어있는 리스트
        
    # 맨 앞 삽입 methods
    def pushFront(self, key):
    	new_node = Node(key)
        new_node.next = self.head # 현재 head node를 먼저 next로 만들어주고
        self.head = new_node # 그 다음에 head node를 new_node로 재지정
        self.size += 1

    # 맨 뒤 삽입 methods
    def pushBack(self, key):
    	v = Node(key)
        if len(self) == 0: # 빈 리스트 ➡️ head node이자 tail node
        	self.head = v
        else:
        	tail = self.head
            while tail.next != None: # head node부터 next를 쫓으며 tail node까지 찾음
            	tail = tail.next
            tail.next = v
        self.size += 1
    
    # 노드 개수 출력하는 길이 methods
    def __len__(self):
    	return self.size

L = SinglyLinkedList()
L.pushFront(-1) 
L.pushFront(9)
L.pushFront(3)
L.pushFront(5)
L.pushBack(4)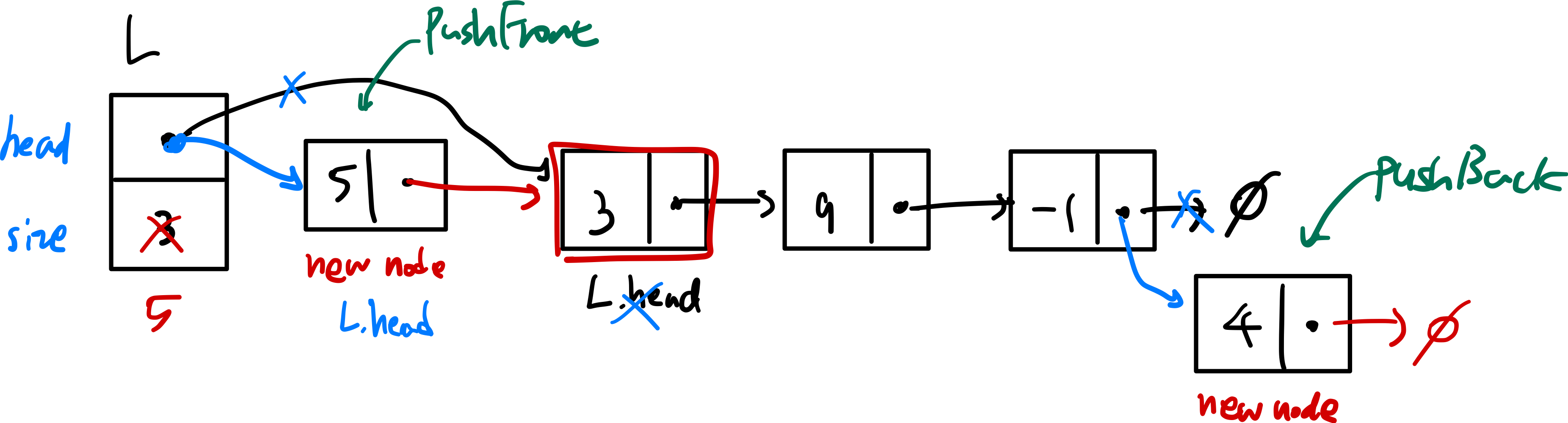

• 위 연결리스트 삽입 순서
  • -1 $\to \emptyset$
  • 9 $\to$ -1 $\to \emptyset$
  • 3 $\to$ 9 $\to$ -1 $\to \emptyset$
  • 5 $\to$ 3 $\to$ 9 $\to$ -1 $\to \emptyset$
  • 5 $\to$ 3 $\to$ 9 $\to$ -1 $\to$ 4 $\to \emptyset$

1-2. 삭제 연산: popFront, popBack

• popFront: 현재 리스트의 head node 앞에 새로운 노드 삽입
• popBack: tail node 다음에 새로운 노드 삽입

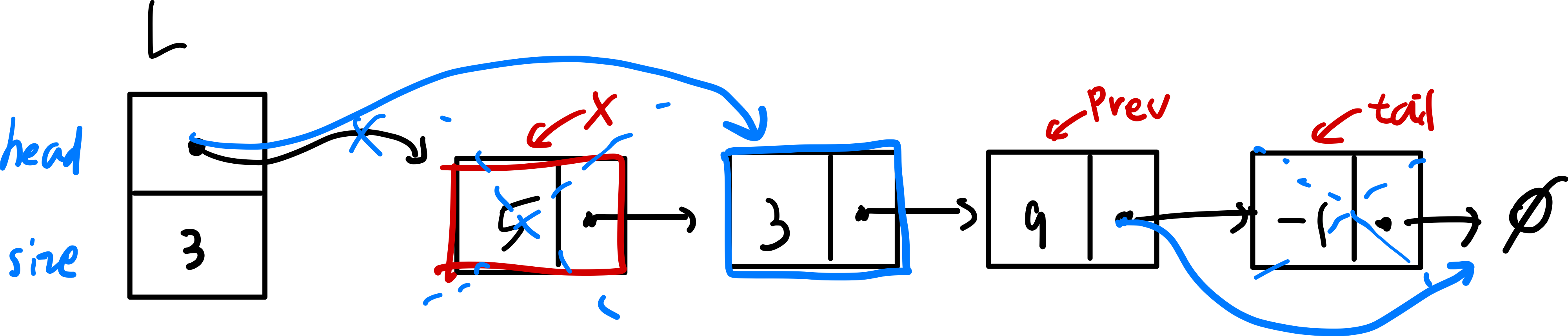
def popFront(self):
	if len(self) == 0: # 지우고 싶은 노드가 없을 수 있음, empty list
    	return None
    else: # 하나 이상의 노드 존재
		x = self.head
        key = self.key # return 해주기 위해 copy
        self.head = x.next
        self.size -= 1
        del x # 메모리 상에서 객체 완전히 삭제
        return key
        
def popBack(self):
	if len(self) == 0 : return None
    else:
    	# running technique
        prev, tail = None, self.head # 징검다리처럼
        while tail.next != None:
        	prev = tail
            tail = tail.next
        
        if len(self) == 1: # 리스트에 노드가 1개 -> 즉 head이면서 tail인 경우는 tail node가 삭제되면 head node는 None을 가리킴
        	self.head = None
        else:
          prev.next = None # or prev.next = tail.next
          key = tail
          self.size -= 1
          del tail
          return key
        

1-3. 한방향 연결리스트의 삽입, 삭제의 시간복잡도

• pushFront, popFront: $O(1)$
• pushBack, popBack: $O(n)$
  • n개의 노드가 있다면 n개 노드를 모두 쫓아가는 시간 필요

1-4. 한방향 연결리스트 추가 연산: 탐색(search) + 제너레이터(generator)

• search: 찾고싶은 노드가 있는지 탐색 ➡️ $O(n)$

def search(self, key):
	# key 값의 노드를 return, 없으면 None return
    v = self.head
    while v != None:
    	if v.key == key: return v
       	v = v.next
    return None # or return v

• generator: 리스트에서는 반복문을 통해 모든 원소를 출력하는데, 한방향 연결리스트에서도 for loop을 통해 리스트 연산처럼 쓸 수 있도록 하는 것 ➡️ special method __iterator__ 선언

def __iterator__(self):
	v = self.head
    while v != None:
    	yield v
        v = v.next
    return StopIteration

• yield가 있는 함수를 generator라고 함
  • for x in L: ~ 처럼 쓸 수 있음
  • 이때 어떤 x인지 모를 때 L이라는 객체에 속한 __iterator__ 를 호출
  • 여기서 yield == return ➡️ v가 x로 return 되어서 print(x)가 가능해짐

---

2. 양방향 연결리스트 (Doubly Linked List)

• 한방향 연결리스트의 단점: 한쪽 방향으로만 연결되어 tail 노드에서 그 앞 prev 노드로 갈 수 있는 방향이 없기때문에 head node에서 순서대로 링크를 타고 찾아야 함 ➡️ $O(N)$

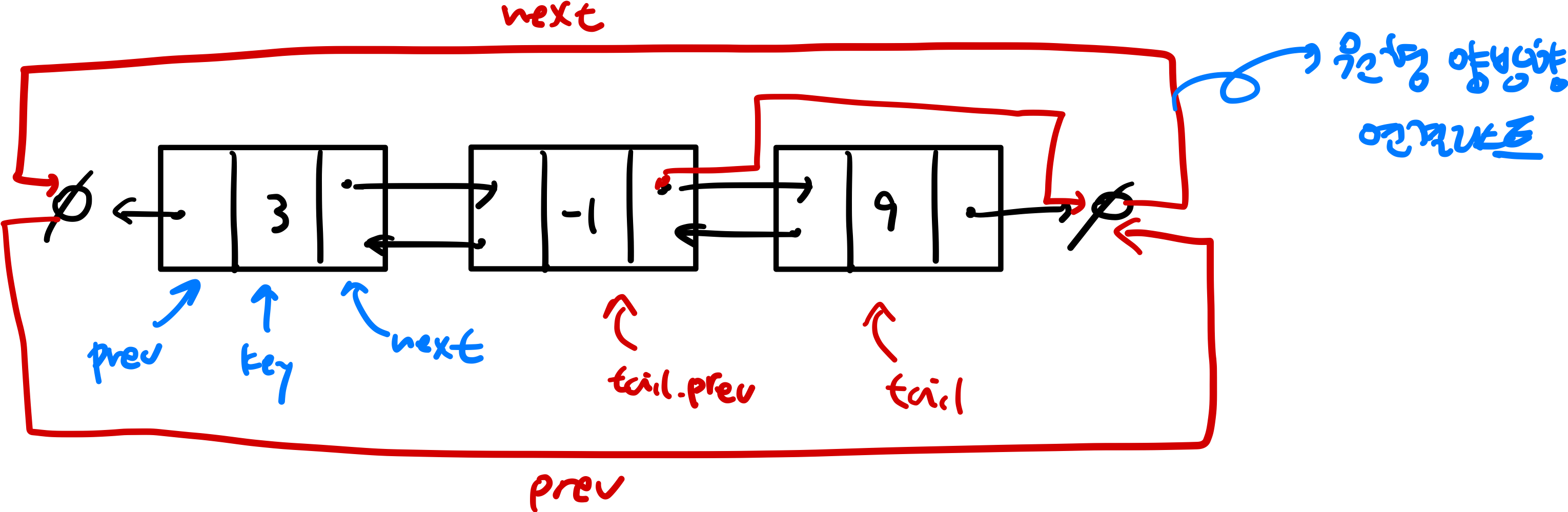
• 양방향 연결리스트의 노드
  • key (value)
  • next (->)
  • prev (<-)
• 단점: 관리해야 할 링크가 prev, next로 2배가 됨 ➡️ 그렇지만 이 복잡도에 비해 상수 시간의 노드 삭제가 가능

원형 양방향 연결리스트 (Circularly Doubly Linked List)

• tail.next가 head를 가르키고, head.prev가 tail을 가리키도록
• 지금부터 양방향 연결리스트를 원형 양방향 연결리스트라고 생각
• 원형 연결리스트에서의 빈리스트: 시작이 어느 노드인지 표기하기 위해 dummy node 하나를 집어 넣음
  • key=None, node.next = 자기자신, node.prev = 자기자신
• 이 dummy node가 일종의 head node 역할 ➡️ 노드가 추가된다면 dummy node를 제일 head node로 두고, head node.prev = tail, tail.next = head로 둔다

노드 클래스 정의

class Node:
	def __init__(self, key=None):
    	self.key = key
        self.next = self
        self.prev = self

class DoublyLinkedList:
	def __init__(self):
    	self.head = Node() # dummy node 하나를 만들고 그것을 가르킴 (Key=None)
        self.size = 0
        
    # def __iter__():
    # def __str__():
    # def__len__():

2-1. splice 연산

• 양방향 연결리스트에서 다양한 종류의 삽입, 삭제 ➡️ splice 연산을 계속 호출하여 사용한다

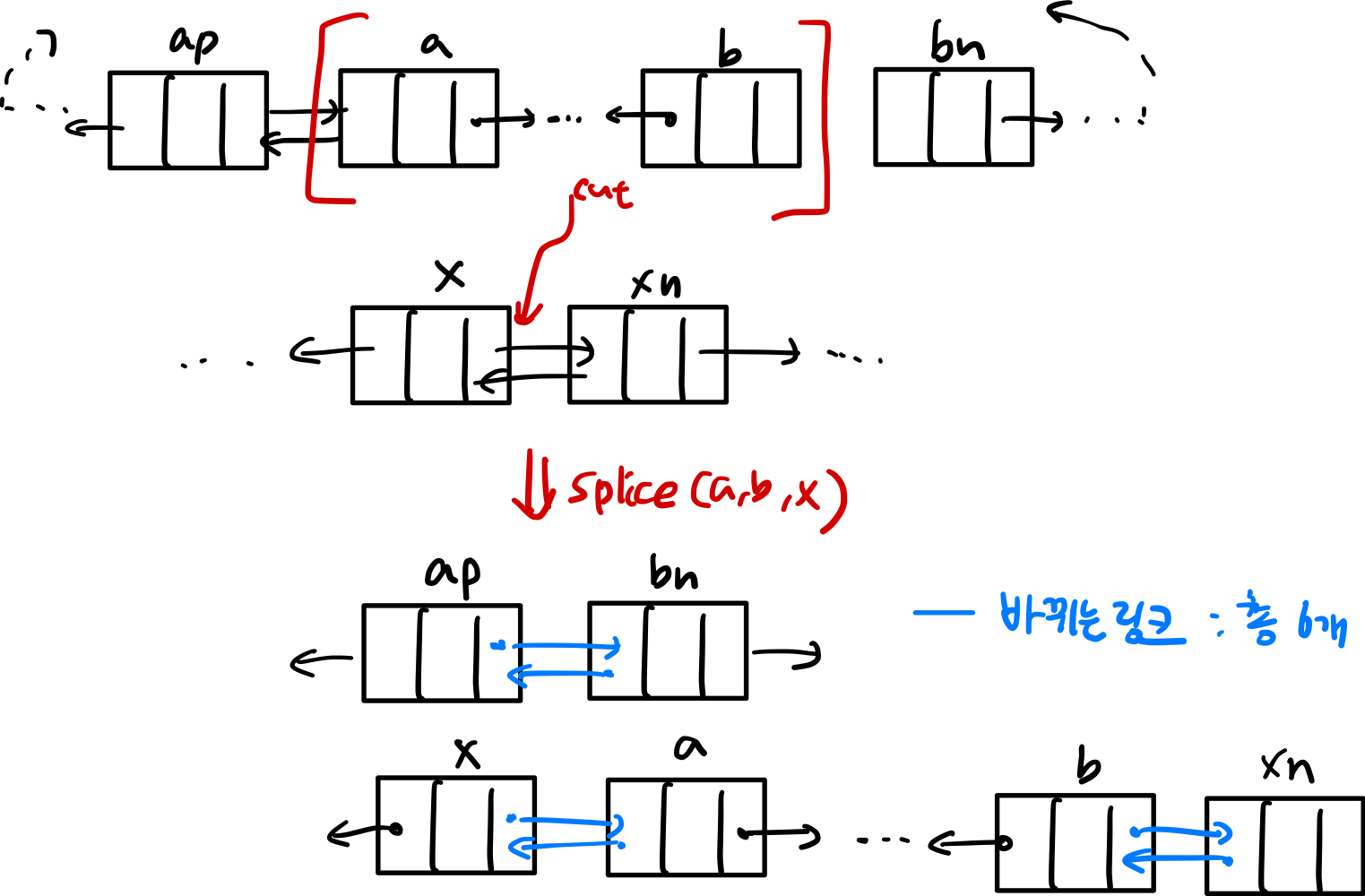
def splice(self, a, b, x): # 3개 노드 a, b, x
	ap = a.prev
    bn = b.next
    xn = x.next
    ap.next = bn # cut한 뒤
    bn.prev = ap # cut한 뒤
    x.next = a
    a.prev = x
    b.next = xn
    xn.prev = b

• 조건 1: a를 따라가다 보면 b가 있어야 한다 (a와 b가 같을 순 있는데, 순서상 a 다음에 b가 나와야 함)
• 조건 2: a와 b 사이에 head 노드와 x노드가 없어야 한다
• [a, b] 사이를 cut해서 x 노드 다음으로 붙여넣음

2-2. 이동 연산

• moveAfter(a, x): 노드 a를 노드 x 다음으로 이동

  • a를 떼서 x 다음으로 splice 연산
  • ➡️ splice(a, a, x)

• moveBefore(a, x): 노드 a를 노드 x 이전으로 이동

  • ➡️ splice(a, a, x.prev)

2-3. 삽입 연산

• insertAfter(x, key)
  • key를 가지는 new node 생성 후 x 노드 다음으로 삽입
  • moveAfter(Node(key), x)
• insertBefore(x, key)
  • key를 가지는 new node 생성 후 x 노드 이전으로 삽입
  • moveBefore(Node(key), x)
• pushFront(Key)
  • insertAfter(self.head, key)
• pushBack(Key)
  • `insertBefore(self.head, key)

꼬리물기 느낌 ..!

2-4. 탐색 연산

def search(self, key):
	v = self.head # dummy node
    while v.next != self.head:
    	if v.key == key:
        	return v
        v = v.next
   	return None

2-5. 삭제 연산

def remove(x): # 노드 x를 삭제
	if x == None or x == self.head:
    	return
    x.prev.next = x.next
    x.next.prev = x.prev
    key = x
    del x
    return key

• popFront, popBack: remove() 사용
• ex) key 값이 5인 노드를 삭제: remove(search(5))

그 밖의 다른 함수

• join(): 두 연결리스트를 하나의 연결리스트로 합침
• split(): 하나의 연결리스트를 어떤 한 노드를 기준으로 두 개의 연결리스트로 분리

2-6. 원형 양방향 연결리스트의 연산의 시간 복잡도

• n개 노드를 갖는 이중(양방향) 연결 리스트라고 가정

• search(key): $O(n)$

• splice(a,b,x): 6개 링크 수정, $O(1)$

  • moveAfter, moveBefore, insertAfter, insertBefore, pushFront, pushBack 모두 splice()를 이용하므로 동일하게 $O(1)$

• remove(x): x 기준으로 이전, 다음 노드의 링크만 수정하면 되므로 $O(1)$

  • popFront, popBack 모두 remove()를 이용하므로 동일하게 $O(1)$
  • 그런데 remove 부르기 전에 search()를 불러서 그 노드를 찾아야하므로 여기서 시간이 오래걸림

• 한뱡향 연결리스트에서는 popBack, pushBack 같은 함수는 $O(n)$ 시간이 걸렸음