
본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1
해시테이블
-
매우 빠른 평균 삽입/삭제/탐색 연산 제공
-
dictionary: (key, values) 쌍으로 이루어진 데이터 구조 ( {} )
- 삽입/삭제/탐색 연산의 효율성에서 좋지 않다
-
순차적으로 저장하지 말고 삽입/삭제/탐색을 쉽게 할 수 있도록 저장해보자 ➡️ 해시 테이블
-
ex) key=2019317, value="신창수"
- key 값을 몇 번째 index에 저장할지 정함
- ex)
index = 2019317 % 10(10개의 저장공간이 있다고 할때) - 10번째 index에 (2019317, "신창수")가 저장됨
- 탐색할 땐
index = 2019317 % 10를 이용해 값이 있나 없나 확인 가능
-
key 값을 index로 mapping
-
위 예시에선 나머지 함수
-
f(key) = key % m- f: 해시 함수 (hash function)
-
-
어떤 key 값을 저장할 공간에 이미 다른 key값이 저장되어있는 경우 ➡️ 충돌, collision
- collision resolution method: 충돌 시 다른 공간에 저장할 방법
해시 테이블의 3가지 요소
1. Table: list
2. Hash function
- key 값을 어떤 hash function에 따라 index로 mapping할 지
3. Collision resolution method
- 충돌 시 어떻게 해결할 것인지
➡️ hash function을 어떻게 정의하고, 충돌 시 resolution method를 어떻게 정의할 것인지에 따라 성능이 좌우됨!
해시 함수 (Hash function)
-
해시 테이블 H에 각각의 저장공간을 slot이라고 함
-
해시 테이블 H의 크기 = slot의 개수 = m (보통 2의 몇 승)
-
Division hash func: 나머지 연산의 해시 함수
f(k) = k % mf(k) = (k % p) % m: p는 소수
-
perfect hash func: key 값들이 slot에 골고루(충돌 일어나지 않고 one-to-one 매핑) ➡️ ideal hash func, 비현실적
-
universal hash func:
-
f(x) == f(y): collision이 발생한 경우 -
p(f(x) == f(y)) = 1/m: 충돌이 발생할 확률이 1/m (해시테이블 크기) -
이것도 설계가 상당히 어려워 조금 더 제한을 약화시킨 것이 c-universal
p(f(x) == f(y)) = c/m(c > 1)
-
-
Division
-
Multiplication
-
Folding
-
Mid-squares
-
Extraction
위 해시 함수들은 해시 테이블을 어느 어플리케이션에 사용할 것이냐에 따라 선택해서 사용
좋은 Hash function이란
1. less collision: 충돌이 적은 해시 함수
2. fast computation: 계산이 복잡해 시간이 오래 걸리는 게 아니라, 가능한 빠른 계산을 만족하는 해시 함수
but, 위 둘은 trade-off 관계가 있으므로 적절히 균형을 맞춰서 효율적인 hash function을 만들어야 한다.
충돌 회피 방법 (Collision Resolution Method)
Open addressing
현재 충돌이 일어났을 때, 그 주위에 있는 빈 공간을 찾아서 저장시키는 방법
probing 방법: 주위 다른 slot을 찔러봄으로써, 살펴봄으로써 대체 공간을 찾는다
-
linear probing 방법
-
충돌이 일어나면 바로 밑의 slot 살펴보고, 그 slot도 차 있으면 또 바로 밑의 slot 살펴보고 ➡️ linear하게 탐색하여 처음 나타난 빈 slot에 아이템 저장
key 값들이 연속된 slot에 모여 있는 형상: Cluster
- cluster가 많이 있으면 안되고, 사이즈가 커도 안돼 (그만큼 탐색 및 삽입에 많은 시간 소요하므로)
-
-
quadratic probing 방법
-
double hashing 방법
chaining (<-> open addressing)
연산의 종류
-
`set(key, value=None)
- 삽입 함수
- key 값이 H에 있으면 value로 update
- key 값이 H에 없으면 (key, value)를 insert
-
remove(key)- 삭제 함수
- key 값을 가진 아이템을 찾아서 그 slot을 삭제
-
search(key)- key 값에 해당하는 아이템이 있는지 찾아서, 있으면 (key, value)를 리턴하고 없으면 None을 리턴
set, search, remove 연산
- 수도 코드
def find_slot(key):
# key 값이 있으면 slot 번호 리턴
# key 값이 없으면 key 값이 삽입될 slot 번호 리턴
i = f(key)
start = i
while (H[i] == occupied) and (H[i].key != key)
i = (i + 1) % m
if i == start: # 한바퀴 다 돌았다 -> 계속 slot이 차 있고 내가 찾는 key가 없어
return Full
return idef set(key, value=None):
i = find_slot(key)
if i == Full: # 저장 못해
# H의 용량을 키워야 함
return None
if H[i].is occupied: # 이미 key 값이 저장되어있다면
H[i].value = value # 새 value로 update
else: # 빈칸
H[i].key, H[i].value = key, value
return key-
search 함수도 set 함수와 마찬가지로
- `if H[i].is occupied:`이면 내가 찾는 key가 있다는 것이므로 return Trueelse:면 없다는 것이므로 return False
-
remove 연산이 제일 까다로움
-
ex) 어떤 값을 찾아서 그 slot 3번을 지웠다면, 나중에 slot 4번에 있던 다른 어떤 값을 search할 때 탐색 시 remove로 지운 값의 slot 3번이 비어있기 때문에 해시 테이블 H에 내가 찾는 값이 없다고 return 됨
-
따라서 slot 3번을 지운 후에, 그 slot 바로 아래 slot 4번에 어떤 값이 있다면 방금 지운 slot 3번 위치로 옮겨줘야함
-
이때! 또 그 밑에 있던 다른 값 slot 5번(이하)은 위치를 바꾸면 안되고 그대로 두어야 함, 왜냐하면 slot 4번에 의해서 slot 5번으로 위치된게 아니라 원래 처음부터 slot 5번에 위치되었기때문에 나중에 slot 5번을 못 찾을 수가 있음
-
근데 만약 slot 7번 자리에 C2가 있었어. 원래 C2 자리는 slot 2번에 위치해야하는데 이미 occupied 되어서 밀리고 밀려서 slot 7번에 위치하게 된 것
-
이러한 경우에는 위에 비어있는 slot 2번으로 위치 이동을 해주어야 함
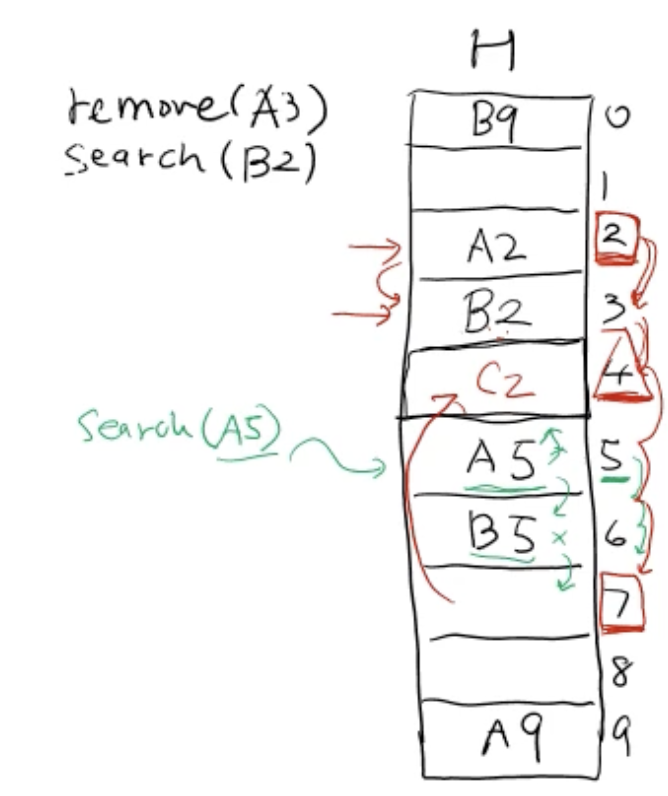
-
k < i <= j, i < j < k, j < k < i
- i는 빈칸 index, k는 f()에 따라 원래 저장되어야 할 index, j는 현재 index (해시 테이블: 원형)
-
def remove(key):
i = find_slot(key)
if H[i] is unoccupied: # 비어 있다 -> 지우고자하는 key값이 저장되어 있지 않음
return None
j = i # 빈 곳을 메꿀 아이템을 찾자, H[i]: 빈 slot, H[j]: 이사해야 할 slot
while True:
H[i] = None
while True: # H[j] 찾기
j = (j + 1) % m
if H[j] is unoccupied: 이사할 게 없고 비어 있다
return key # remove 함수 완료
k = f(H[j].key)
if not (i < k <= j or j < i < k or k <= j < i) : break # 테이블의 슬롯이 원형으로 연결되어 있기 때문에 i와 j의 대소관계에 따라 옮기면 안되는 3가지 경우를 정의
H[i] = H[j]
i = j # i는 항상 빈 slot을 나타내므로 다시 j를 대입
- linear probing: 한 칸씩 아래로 내려가면서 내가 찾을 key가 있는지 탐색
- cluster의 마지막 빈 자리에 저장하기 때문에 cluster의 크기가 1씩 증가하는 단점
- quadratic probing: 한 칸씩 말고 제곱한 수 만큼 더해서 건너 뛰어보자
- ... $ k -> k + n^2$
- linear probing보다 cluster 사이즈가 더 늦게 증가하지만, remove 할 때 제곱으로 건너 뛰므로 더 복잡해짐
- double hashing: hash 함수 2개 사용
- f(), g()
- f(key)가 만약 occupied 되었따면 f(key) + g(key)
- f(key) + g(key)도 occupied 되었다면 f(key) + 2g(key) (2배, 3배 ... 하여 index를 구함)
- hash 함수 2개 마련 및 계산이 필요하다는 점
- set, remove, search 함수는 cluster size가 영향을 미치는데, cluster size는 hash function과 collision resolution method, load factor의 영향을 받음
- load factor: n / m (0 <= n/m < 1)
- m: slot 전체 개수
- n: H에 저장된 item의 개수 (최소 n번의 set이 이루어졌다는 것)
- load factor가 1에 가까울 수록 빈 slot이 없으므로 collision이 더 발생
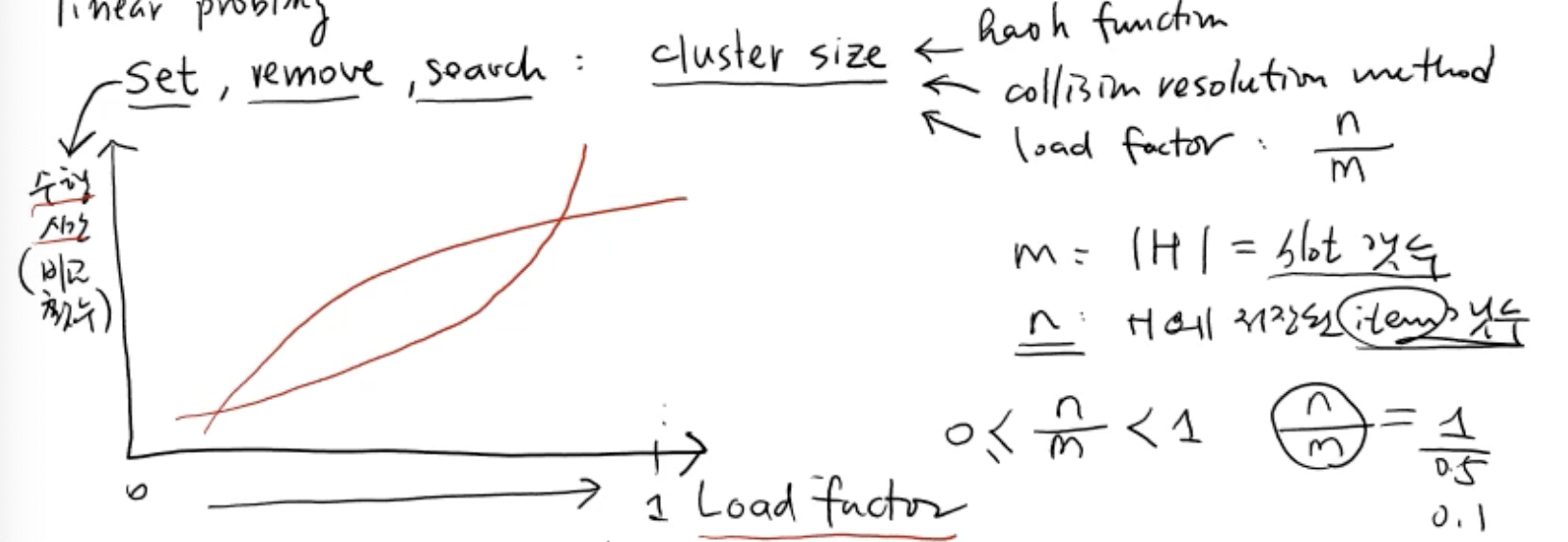
- cluster size는 평균적으로 , 즉 최소 50% 이상 빈 slot인 경우를 만족하게 한다면, cluster의 평균 size가 항상 를 만족할 수 있다.
Chaining
- 각 slot에 한방향 연결리스트를 만듦

