본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1
그래프(Graph) 정의
- 가장 복잡한(일반적인) 자료구조
G=(V,E)V: vertex(node) set, 정점E: edge, 링크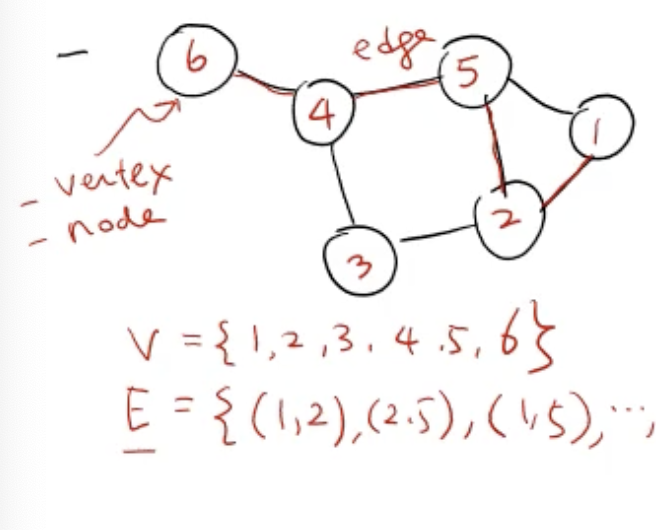
-
degree(인접성): 노드의 edge 개수, ex) degree(4)=3, degree(1)=2, ... ➡️ degree(G)=3 (max값)
-
edge(4, 5) = 노드 4와 노드 5는 인접하다 (adjacent)
-
경로(path): ex) 3에서 5로 가는 path는 [3 ➡️ 2 ➡️ 5], [3 ➡️ 2 ➡️ 1 ➡️ 5], ...
- 중복되면 안됨
-
사이클(cycle): 어떤 노드에서 출발해서 제자리로 돌아오는 닫힌 경로, ex) [3 ➡️ 2 ➡️ 5 ➡️ 4 ➡️ 3]
-
그래프에서 사이클이 없을 수도 있고, 많을 수도 있다
-
사이클이 없는 그래프 = 트리: 부모-자식 관계의 edge만 존재하므로
- 사이클이 없다는 것은 두 노드를 잇는 경로가 유일하다는 것, 사이클이 있으면 두 노드를 잇는 경로가 2개 이상일 수도 있지 (e.g. 3 ➡️ 5의 경로)
-
-
방향성이 없는 그래프(=양방향 그래프): undirected graph
-
방향성이 있는 그래프(=방향 그래프): directed graph, edge에 화살표가 존재
그래프(Graph)의 표현법
- 인접성을 표현 1. 인접 행렬 (adjacency matrix)
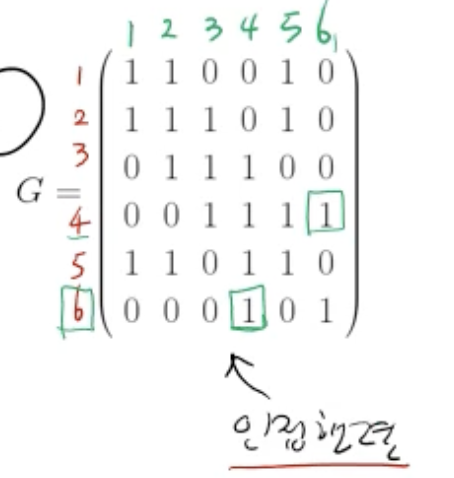
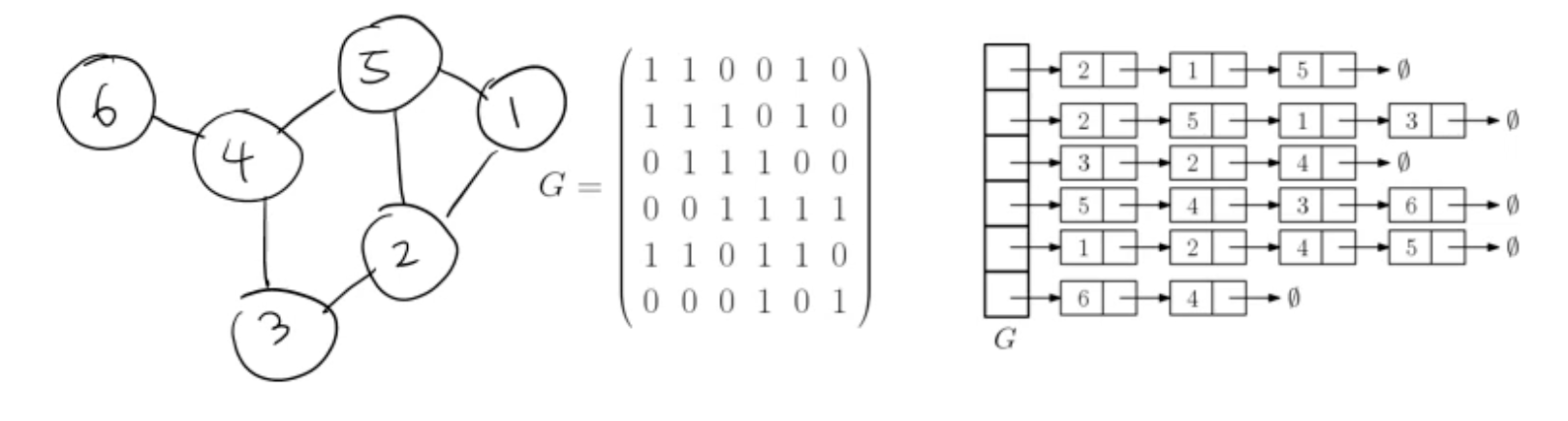
- 노드들 사이의 edge가 존재하면 1, 존재하지 않으면 0
- 대각선 값 1: 자기 자신으로의 경로가 있다고 보면 1, 없다고 보면 0 (정의하기 나름)
- 단점: 행렬에 entry가 존재 ➡️ 만약 그중 edge 1개만 존재할 경우 반 이상이 정보가 없는 것을 표현하기 위한 메모리가 사용돼 낭비됨
2. 인접 리스트 (adjacency list) (이때 list는 연결리스트)
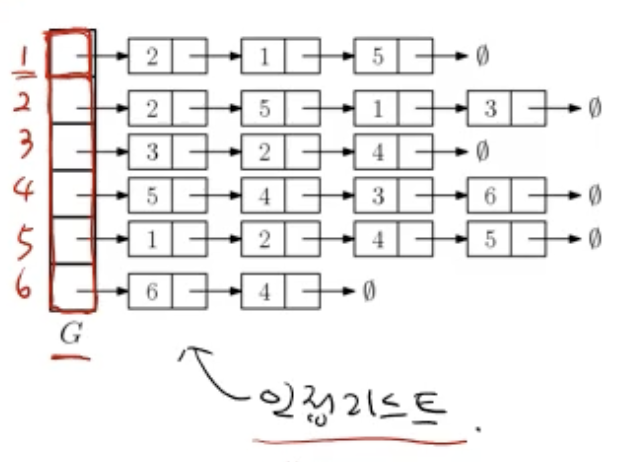
- 각 vertex가 자기 만의 연결 리스트를 가지고 있음 (자신과 인접한 vertex들)
- 존재하는 edge만 표현돼 edge 개수의 2배 -> 무방향 그래프라서그래프(Graph) 기본 연산
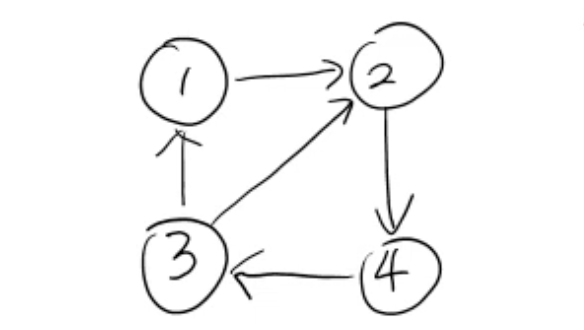
- 방향 그래프
G=(V,E)=(노드 집합, 에지 집합)- 노드 개수:
|V| = n - 에지 집합 크기:
|E| = m
1. 인접 행렬
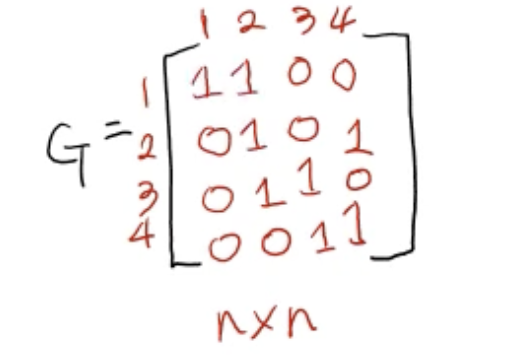
- 에지마다 가중치가 주어질 수 있음 (노드에서 노드로 가는데 드는 cost라고 생각)
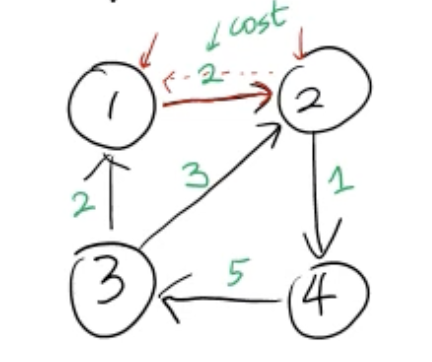
- 그러면 행렬에 1이 아니라 그 가중치를 적어 줌
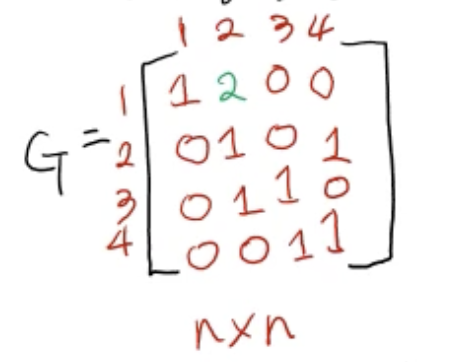
- 그러면 행렬에 1이 아니라 그 가중치를 적어 줌
-
memory:
-
의 edge가 존재하느냐
G[u][v]==1 or G[u][v] > 0: (상수 시간에 가능)
-
에 인접한 모드 노드 에 대해 (어떤 action):
for v in range(1, n+1): do with G[u][v]➡️ -
새로운 에지
(u,v)삽입:G[u][v]=1 (or weight) -
기존
(u,v)삭제:G[u][v]=0
2. 인접 리스트
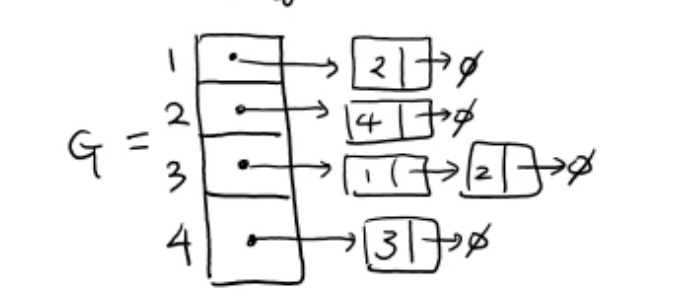
1. memory:
2. 의 edge가 존재하느냐
G[u].search(v): (최악의 경우 모든 노드가 에 연결되어있을 수 있음)
-
에 인접한 모드 노드 에 대해 (어떤 action):
for each edge in G[u]: do something- 인접리스트
G안의each edge==each node➡️ - 인접 행렬에서는 인접 노드 수가 많든 적든 무조건 인 반면, 인접 리스트에서는 인접 노드 개수만큼 방문하면서 action 취함
- 인접리스트
-
새로운 에지
(u,v)삽입:G[u].pushFront(v)➡️- 파이썬 리스트에서는 상수 시간이 아님 ➡️ 그런데 굳이 순서대로 정렬할 필요 없으므로 그냥
.append()를 통해 상수 시간 보장 가능
- 파이썬 리스트에서는 상수 시간이 아님 ➡️ 그런데 굳이 순서대로 정렬할 필요 없으므로 그냥
-
기존
(u,v)삭제:x=G[u].search(v)G[u].remove(x)➡️ (삭제할 노드 찾는데 걸리는 최악의 시간)
결론
-
메모리 측면에서는 인접 행렬 () << 인접 리스트 ()
- 그런데 경우에 따라 인접 리스트도 만큼의 에지가 존재할 가능성도 무시 못해 ➡️ 인접리스트가 오히려 비효율적
-
sparse graph: 노드 개수에 비해 에지 개수가 상당히 적은 경우 ↔️ dense graph
