9-2. Red-Black 트리

본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1

Red-Black 트리

• 가장 유명하고 많이 사용되는 균형이진탐색트리
  
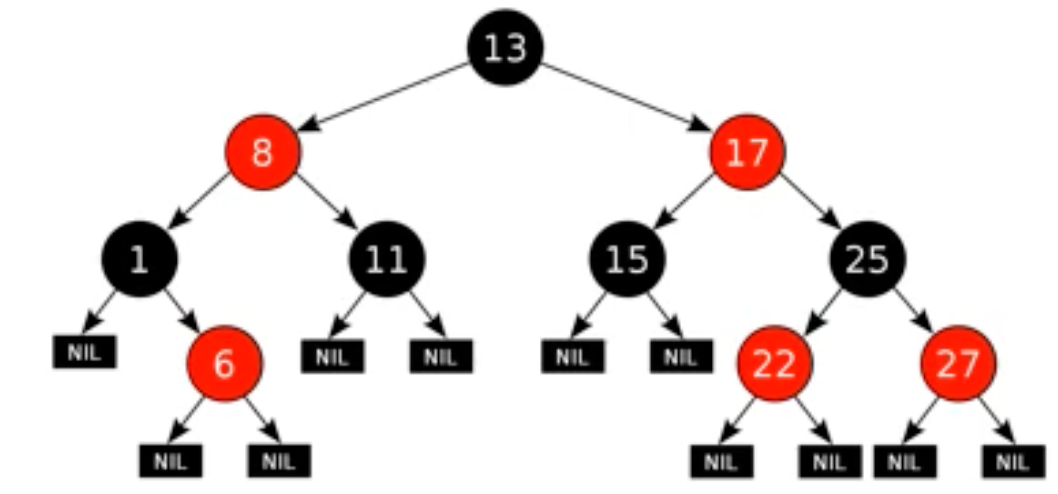
• Leaf Node: Null, None으로 독립적으로 표현할 것임
• Red-Black 트리의 5개의 조건 (당연히 이진탐색트리)
  1. 노드 ➡️ red/black

  2. root 노드 ➡️ black

  3. leaf 노드 ➡️ black

  4. red 노드 ➡️ 자식 노드 모두 black

     • black 노드의 자식은 상관 없다

  5. 각 노드에서 leaf 노드로 가는 경로 중, black 노드의 수가 항상 같아야 함 (red-black 트리의 height가 항상 $log(n)$에 비례하도록 제한할 때 사용되는 결정적 성질)

     • ex) 25번 밑의 leaf 노드로 가는 경로의 수는 4가지, 이때 4가지 각각 black 노드의 수가 2개씩 존재 (25번 + leaf 노드)
       
• red-black 트리도 균형이진탐색트리이기 때문에 높이가 항상 $O(logn)$을 유지해야 하는데, 위 5가지 조건을 만족한 red-black도 이를 만족하는지 증명해보자

O(logn) 증명

• h(v): v의 높이(height)

• bh(v): v는 제외하고, v에서 leaf 노드로 가는 경로 중 black 노드의 개수

  • ex) 위 그림에서 bh(13)=2, bh(25)=1

• fact 1. v의 서브트리의 내부노드 개수 $\ge 2^{bh(v)}-1$

  • 증명: h(v)에 대한 귀납법(induction)

    • $B$: 귀납법은 base case 증명 필요 ➡️ $h(v)=0$ (즉 leaf 노드=None 노드 1개만 존재)
      • 이때 $bh(v) = 0$, v의 서브트리의 내부노드 개수$=0\ge 2^0-1=0$
      • fact 1 부등식 만족
    • $H$: 가정 단계 ➡️ if $h(v) \le k$: $|$v의 서브트리의 내부노드 개수$|$ $\ge 2^{bh(v)}-1$
    • $I$: induction 단계 ➡️ if $h(v)=k+1$일 때 $H$의 부등식이 성립함을 증명

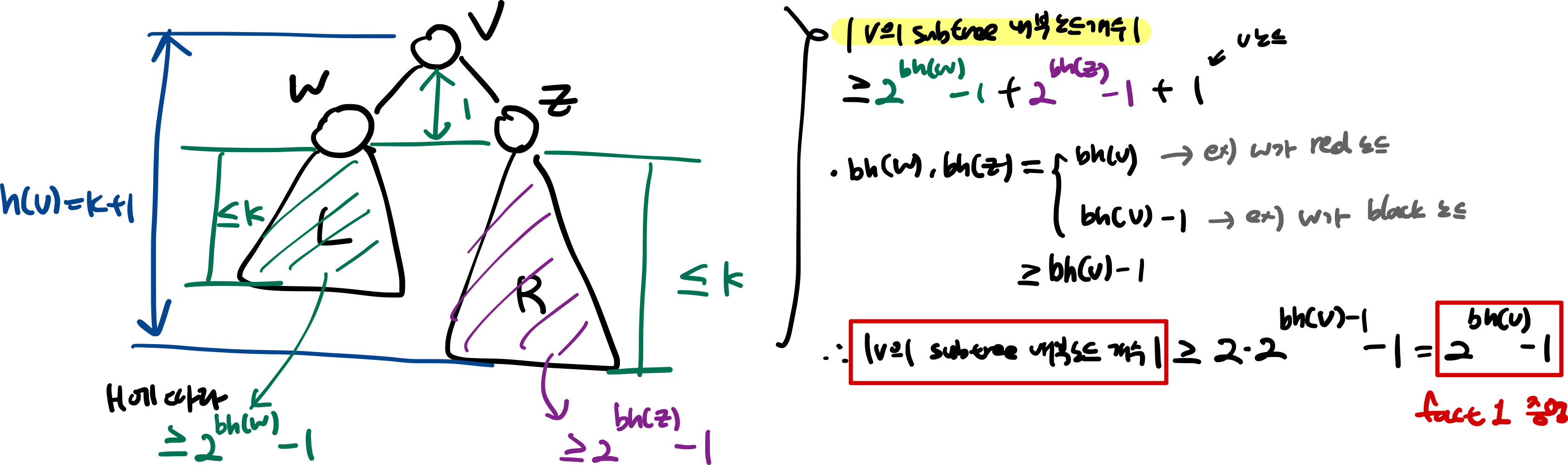
• fact 2. black 노드 수 $\ge \frac{h}{2}$
  

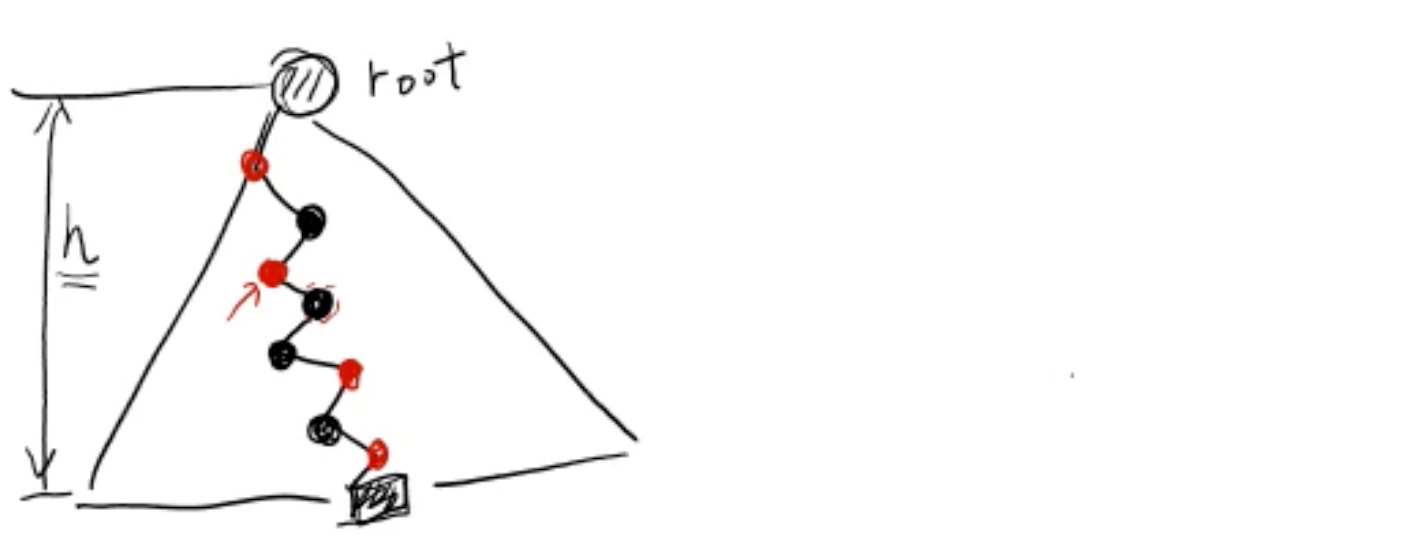
• red 노드의 자식은 항상 black 노드

• black 노드 수는 전체 height의 반 이상 (red 노드 하나에는 최소한 자식은 black이므로 red 노드 개수가 더 많을 수가 없지)

• black 노드 수 = $bh(r)\ge \frac{h}{2}$

• $r$의 subtree의 내부노드 개수 $\ge 2^{bh(r)}-1\ge2^{\frac{h}{2}}-1$

  • 이때 $r$은 red-black 트리의 노드 개수이므로 $\le n$
  • $n\ge2^{\frac{h}{2}}-1$
  • $2^{\frac{h}{2}}-1\le n+1$
  • $\frac{h}{2} \le log_2(n+1)$
  • $h \le 2log_2(n+1)$ ➡️ 즉 $h$는 아무리 커봤자 $2log(n)$밖에 안된다는 것

• 따라서 $h=O(log_2n)$을 증명 가능

• 이 증명의 핵심은, red 노드의 자식은 항상 black 노드이다

  • 근데 black 노드는 최소 높이의 반 이상이 존재하는데, 5번의 조건에 따라 어떤 노드에서 시작하든 leaf 노드까지의 black 노드 개수가 항상 일정하므로 트리가 치우쳐져있지않고 균형이 맞춰져있다는 것
  • 이것이 red-black 트리의 아이디어

---

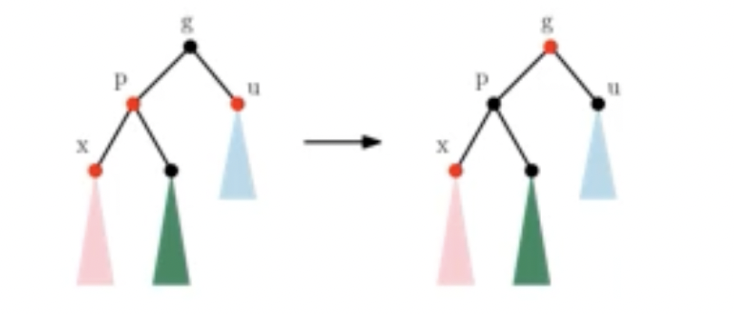
Red-black 삽입 연산 (only Idea)

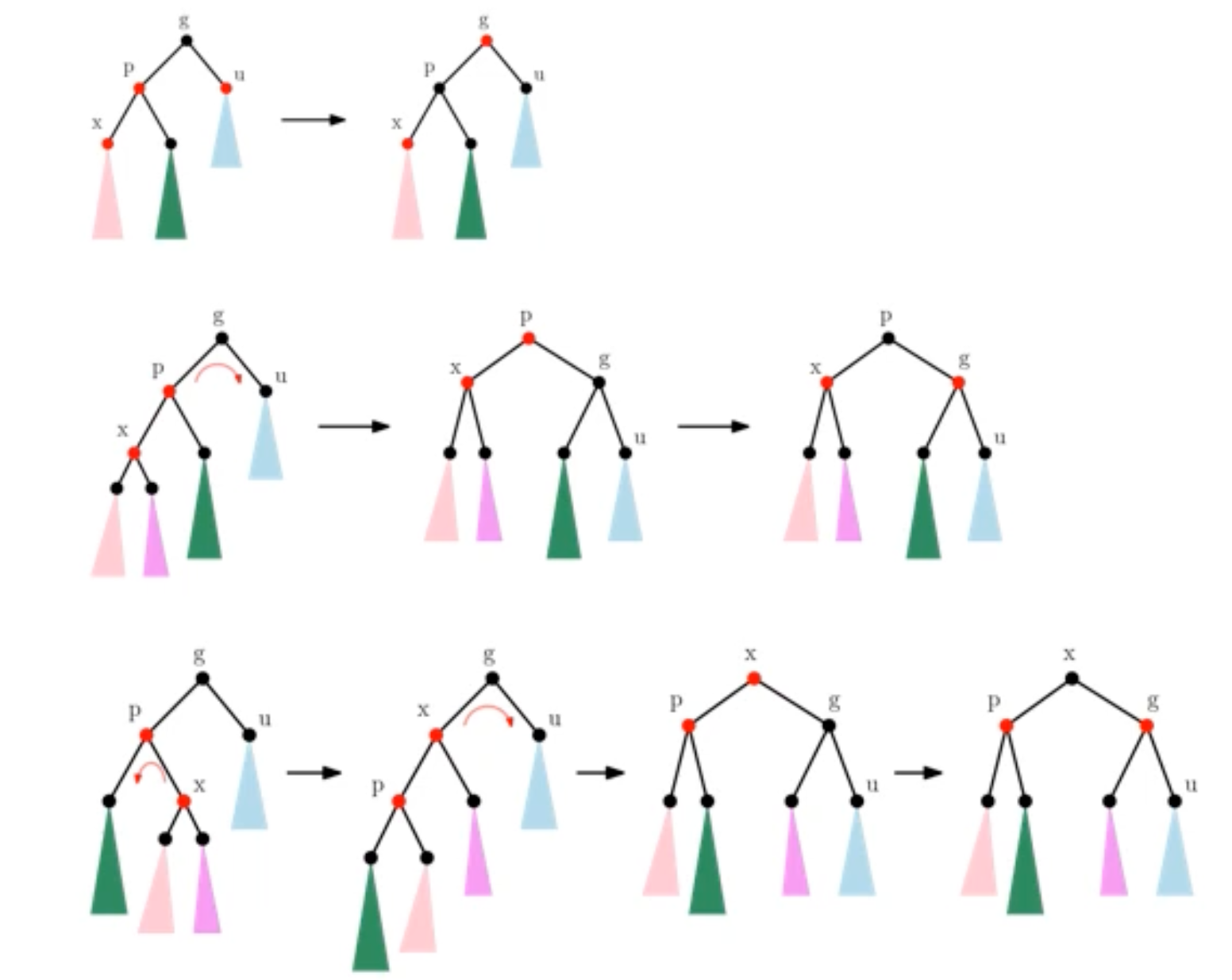
1. BST의 insert 연삽은 호출해 새로운 노드 x를 삽입

2. x.color = red

3. 4가지 경우로 나눠 조정

   a. x=T.root

   • x.color=black

   b. if x.parent.color == black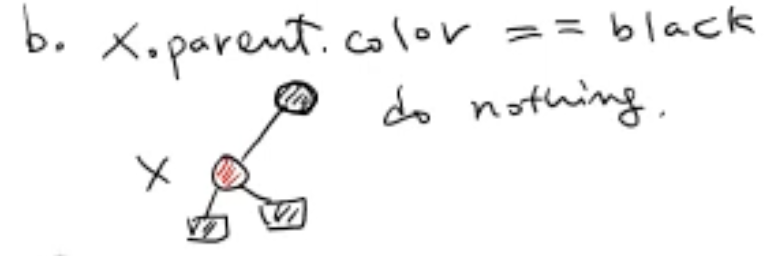

   

   • do nothing

   c. x.parent.color == red

   1. if x.uncle.color == red (uncle: 부모의 형제)
      

---