9. 균형이진탐색트리 (Balanced BST)

본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1

균형이진탐색트리 (Balanced BST)

• 이진탐색트리: 탐색에 적합한 트리 자료구조

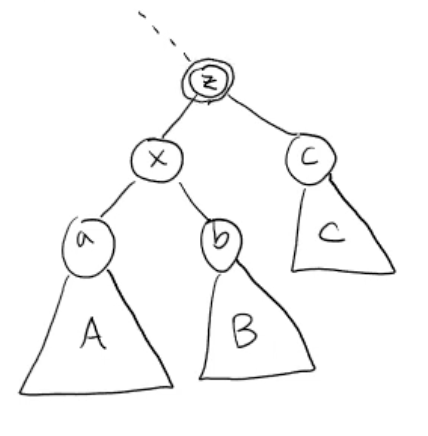
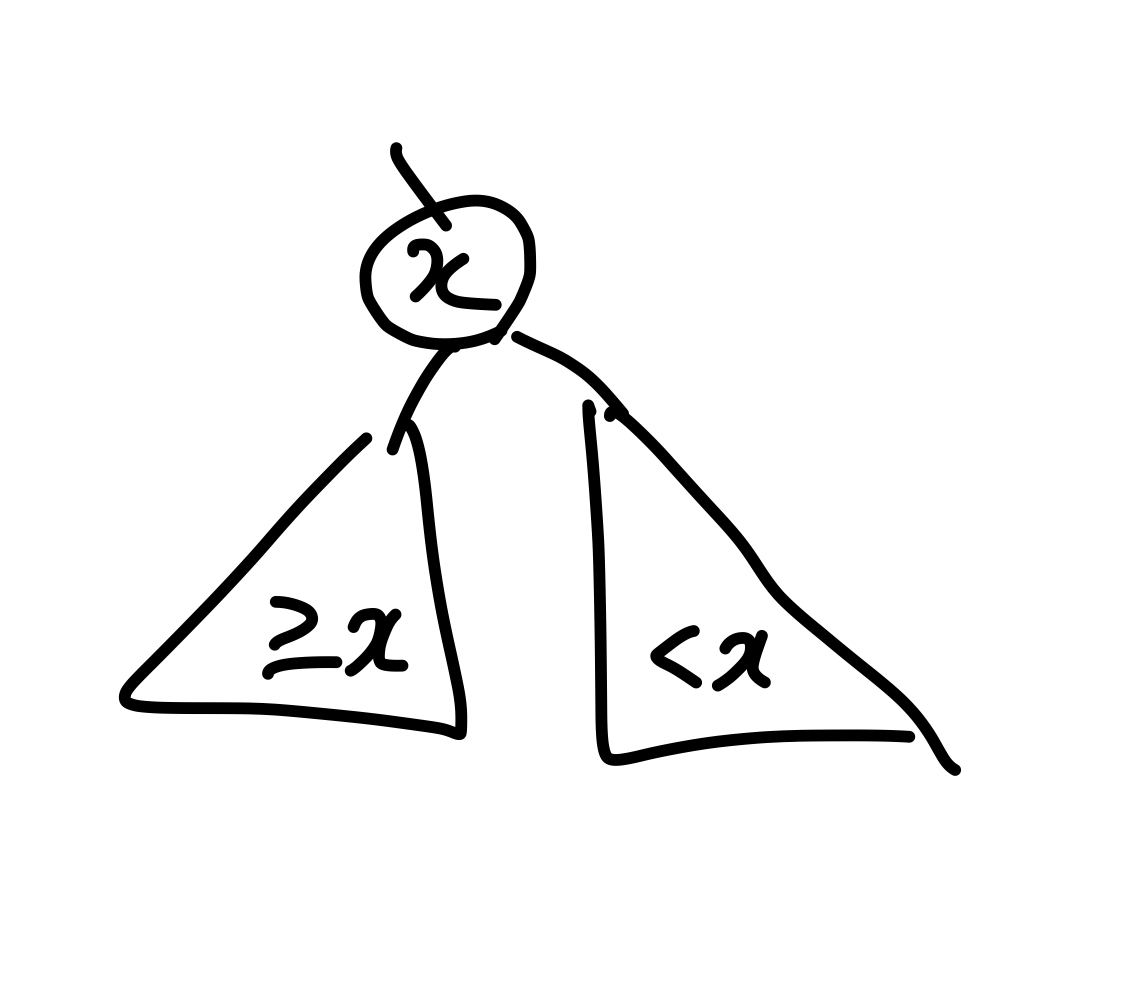
  • 모든 트리에 대해 각 노드의 왼쪽 부트리는 x(부모노드)보다 작거나 같은, 오른쪽 부트리는 x보다 큰 형태를 만족해야 함
    

  • 트리의 높이 $h$라 할 때

    • search: $O(h)$ 시간
    • insert: $O(h)$ 시간
    • delete: $O(h)$ 시간

  • 가장 $h$가 큰 이진탐색트리: 각 노드가 하나씩의 자식 노드만을 가질 때

    
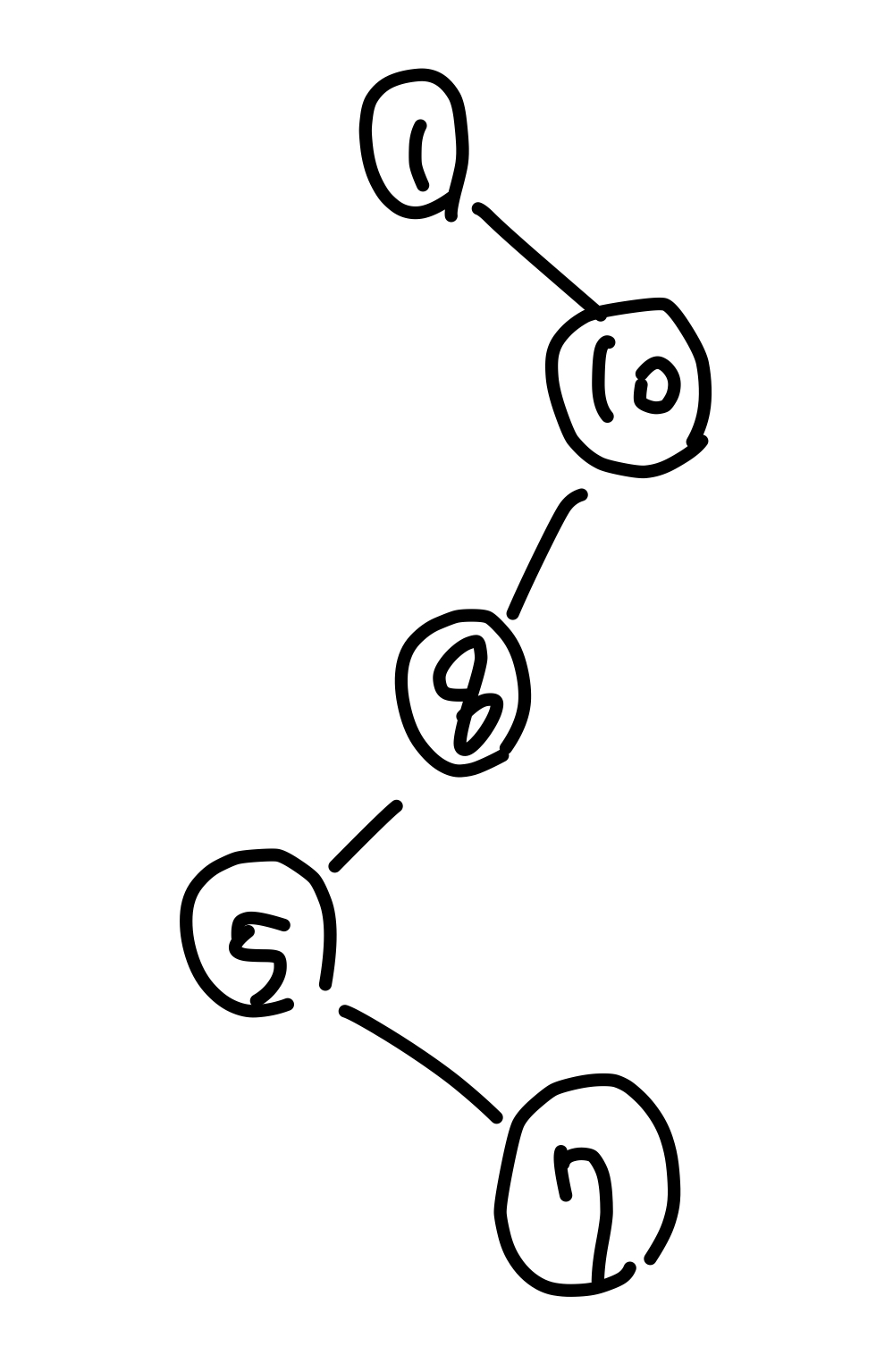
    • 이때 $h$는 $h \le n-1$ 까지 증가 할 수 있다

  • 반대로, 가장 $h$가 작은 이진탐색트리: 노드마다 최대 두개씩의 자식노드를 가질 때 ➡️ heap

    • n개의 노드를 가진 heap의 높이는 $log(n+1) \le h$, 즉 h를 아무리 줄여도 log(n)까지는 줄일 수 있다

    ➡️ 즉, $log(n) \le h \le n-1$

• 트리의 높이 h가 어느정도 커진다고 생각되면, 조정을 통해 트리의 h를 항상 $O(logn)$으로 유지하는 이진 탐색트리를 생각 ➡️ 균형이진탐색트리 (Balanced BST)

  1. AVL 트리 (가장 첫번째)
  2. Red-Black (가장 유명한)
  3. (2,3,4)-Tree (Red-Black과 유사)
  4. Splay Tree

---

• 어떻게 높이를 $log(n)$으로 유지하냐? ➡️ 트리를 수정해서 $O(logn)$이 되도록 강제함
  • 각 트리마다 어떤 기준을 넘어서면 뭔가 조정을 한다는 것
  • 이때 조정하는 연산: Rotation(회전)

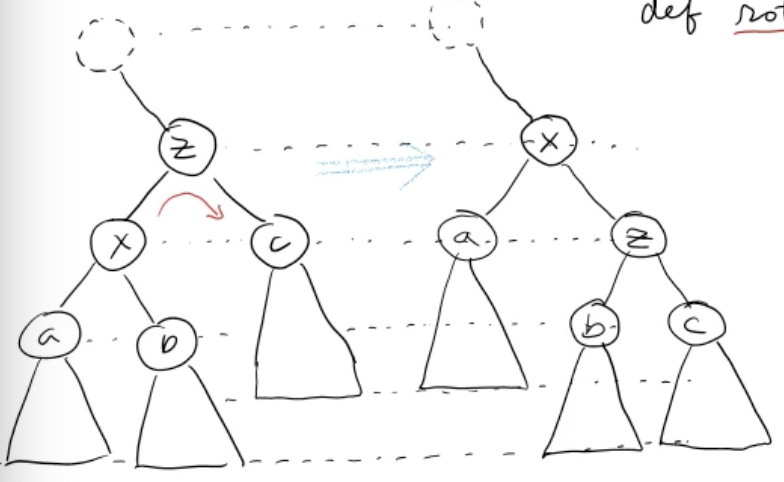
Rotation을 통한 트리 조정

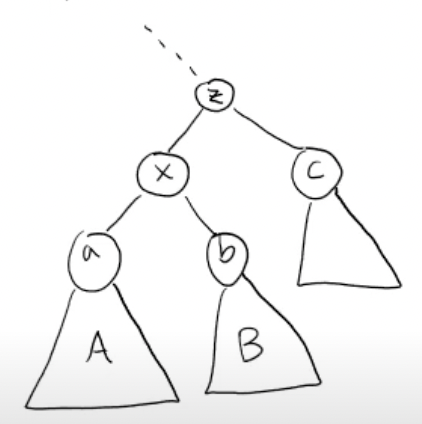
• 현재 위 트리는 BST ➡️ $A \le x < B \le z < C$
• z를 기준으로 right rotation
  • z는 내려가고 z 밑의 subtree들은 한 단계 올라옴

• x가 올라오면서 z는 x의 오른쪽 child가 되고, x에는 왼쪽 child 자리밖에 없으므로 원래 왼쪽 child 였던 A가 붙음

  • B는 원래 트리 크기 $x < B \le z$ 에 따라 z의 왼쪽 child로 붙게 됨

• 최종적으로 원래 z 입장에서의 왼쪽 subtree는 level이 한 단계 올라가고, 오른쪽 subtree는 level이 한 단계 내려가게 되었음

  • 전체적으로 트리의 높이가 한 level이 올라감 (전체 높이 $h$가 한 단계 줄어듦)으로써 트리의 높이 조정

• 바꾸어야 할 링크

  • x의 부모 = z의 부모
  • z의 부모의 오른쪽 자식 = x
  • x의 자식노드 = z
  • z의 부모 = x
  • z의 왼쪽 자식 = b
  • b의 부모 = z

• z를 right rotation 시킨 트리를 다시 left rotation을 하면 원상복구됨

  • left rotation은 그 반대로 오른쪽 subtree level이 하나 올라가고, 왼쪽 subtree는 level이 하나 내려가는 형태

rotateRight 코드

def rotateRight(self, z):
	if not z:  # z=None인 경우
    	return
        
    x = z.left
    
    if x == None: # z의 왼쪽 부트리가 없으므로 올라온 x가 없는 것 -> 변하는게 없지
    	return
        
    b = x.right
    x.parent = z.parent # 링크 수정 1
    if z.parent: # z.parent가 none일 수도 있음(root)
    	# 링크 수정 2
    	if z.parent.left == z: 
        	z.parent.left = x
        else:
        	z.parent.right = x
    
    x.right = z # 링크 수정 3
    z.parent = x # 링크 수정 4
    z.left = b # 링크 수정 5
    if b: # b가 none이 아니면
    	b.parent = z # 링크 수정 6
    
    if self.root == z: 
    	self.root = x # root 노드 정보 수정

---