문제

문제 링크: 프로그래머스-k진수에서 소수 개수 구하기

풀이

진법 변환,소수 판별에 관한 문제이다.

1. 주어진 n을 k진수로 변경
2. 변환된 수를 문자열로 만들고 "0"을 기준으로 분할
3. 분할된 토큰을 십진수로 변환 후 소수 판별

n을 k진수로 변환

n을 k로 나눈 값이 0이 될때 까지 그 나머지를 역순으로 저장

vector<int> number;
    while (n / k > 0) {
        number.push_back(n % k);
        n = n / k;
    } number.push_back(n % k);

소수 판별

에라토스테네스의 체

소수 판별하면 역시 에라토스테네스의 체로 검사해봐야지! 라고 생각했다.
토큰화된 수가 많다면 가장 큰 수 하나만 에라토스테네스의 체로 검사한 뒤 그보다 작은 값들은 자동으로 검사가 되기 때문이다.

uint64_t maxN = *max_element(intToken.begin(), intToken.end());
    
vector<bool> Eratos(maxN+1, true);
Eratos[0] = false;
Eratos[1] = false;
for (uint64_t i=2; i*i < maxN+1; i++){
    if (Eratos[i]) {
        for (uint64_t j=i*2; j < maxN+1; j+=i){
            Eratos[j] = false;
        }
    }
}
for (auto i: intToken){
   if (Eratos[i]){
       answer++;
   }
}

하지만 실패

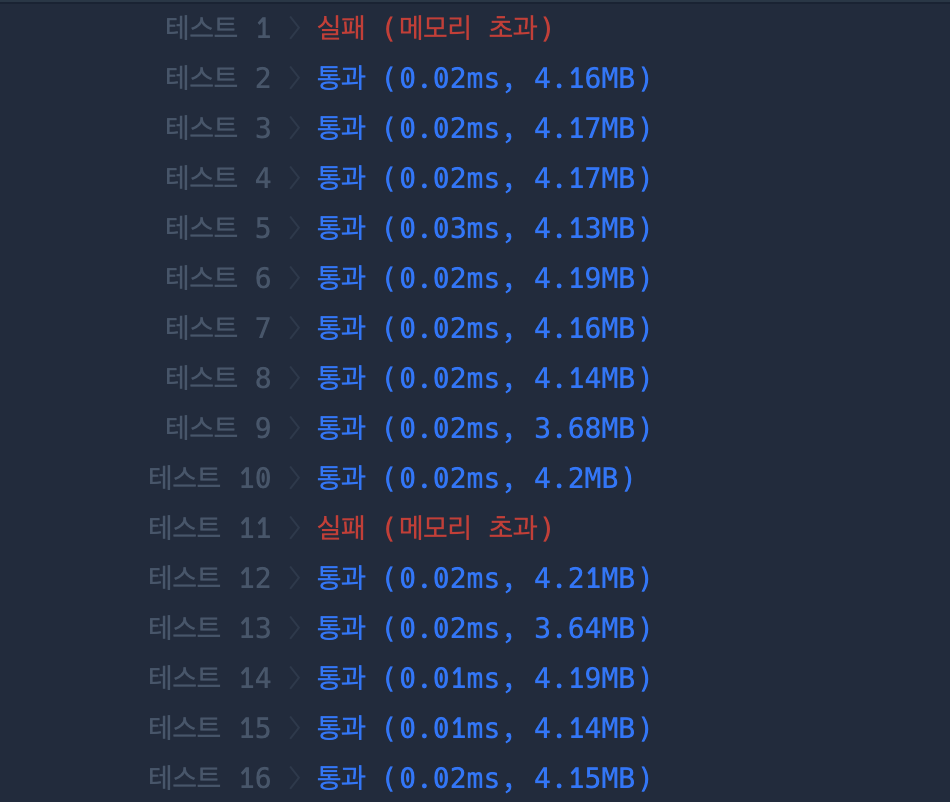
왜 메모리 초과가 생기지?
n 이 1,000,000 이고 k가 3이라면 1212210202001이라는 수가 생긴다.
n이 백만에 가까운 수에 변환된 수에 0이 없다면 조, 억단위의 수를 검사해야 하는 것이다.
위의 코드 처럼 에라토스테네스의 체로 검사하기 위해 길이가 조, 억단위인 bool 배열을 만드니 메모리 초과가 생긴것 같다.

약수 검사

에라토스테네스의 체를 사용할 수 없게 되었으니 1과 자기 자신의 제외한 약수를 가지는 지 검사를 하는 방법으로 소수 판별을 하게 되었다.

bool isPrime(uint64_t n) {
    
    if (n == 2)
        return (true);
    if (n <= 1)
        return (false);

    for (uint64_t i=2; i*i < n+1; i++){
        if (n % i == 0){
            return false;
        } 
    }

    return (true);
}

코드

#include <string>
#include <vector>

using namespace std;

bool isPrime(uint64_t n) {
    
    if (n == 2)
        return (true);
    if (n <= 1)
        return (false);

    for (uint64_t i=2; i*i < n+1; i++){
        if (n % i == 0){
            return false;
        } 
    }

    return (true);
}

int solution(int n, int k) {
    int answer = 0;

    vector<int> number;
    while (n / k > 0) {
        number.push_back(n % k);
        n = n / k;
    } number.push_back(n % k);
    
    string strNum;
    for (int i = number.size()-1; i >=0 ; i--){
        strNum += to_string(number[i]);
    }

    vector<uint64_t> intToken;
    size_t pos;
    while ((pos = strNum.find("0")) != string::npos){
        string token = (strNum.substr(0, pos));
        if (token.length() > 0)
            intToken.push_back(stoul(token));
        strNum.erase(0,pos+1);
    }
    if (strNum.substr(0, pos).length()>0)
        intToken.push_back(stoul(strNum.substr(0, pos)));

    for (auto n: intToken){
        if (isPrime(n))
            answer ++;
    }

    return answer;
}

앞서 설명했지만 판별해야 할 수가 정말 큰 수 있기 때문에 int가 아닌 long long 자료형을 사용해야 했다.