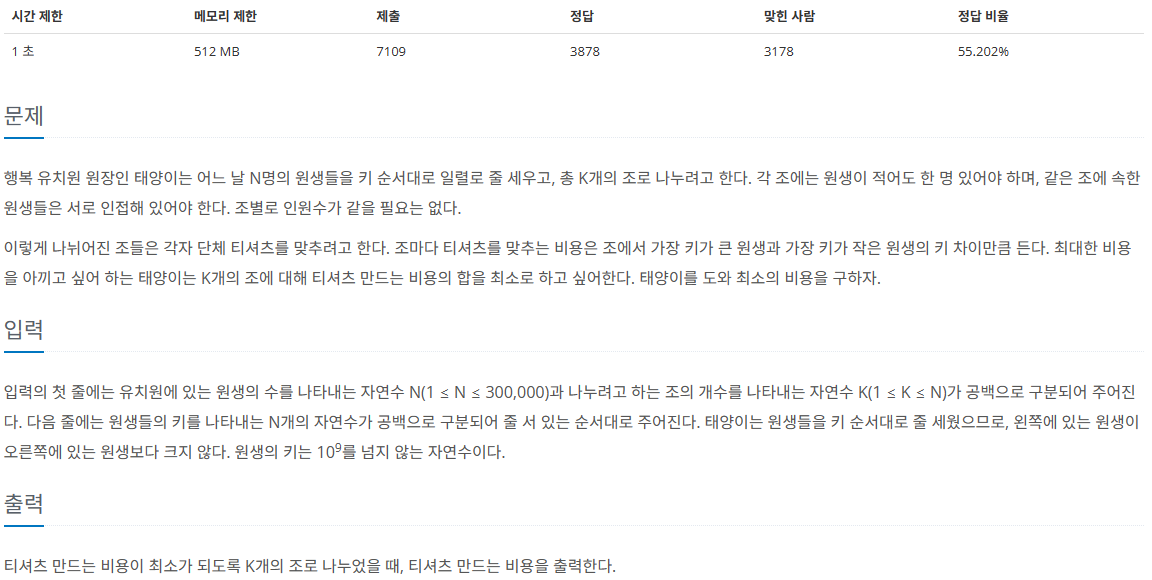
문제

13164번: 행복 유치원

풀이

먼저 티셔츠 만드는 비용의 합을 구하는 방법을 알아봅시다.

입력으로 주어지는 원생들의 키는 정렬되어 있습니다.
총 n 명에 대해서 각 키를

이라 한다면
모든 원생이 한 조일 경우, $cost_1 = a_n - a_1$ 입니다.

만약 i번째와 i+1 번째 원생 사이를 기준으로 두 조로 나누게 된다면 각 조의 (마지막 - 처음)을 더하여 비용을 구할 수 있습니다.

이때 식의 순서를 조금 바꾸어보면

이렇게 변형할 수 있고, 이는 한 조로 나눌때의 비용에 i+1번째원생, i번째 원생의 키 차이를 뺀 값이 됩니다.

마찬가지로

이때 $cost_3$이 최소가 되고 싶다면 $(a_{i+1}-a_{i})-(a_{j+1}-a_j)$ 값이 최대가 되어야 합니다.

이를 편하게 보기 위해 모든 $i$에 대해 $a_i - a_{i+1}$의 값을 저장하여 정렬한 배열을 $b_i$를 정의하겠습니다.
($b_1 > b_2 > b_3 \;\cdots > b_{n-1})$

이제 최소일 때의 $cost_3$, 즉 $minCost_3$를 정의하면

k로 일반화하면

정리하자면 각 이웃한 원생들의 차이를 저장하는 배열을 만들고,
가장 큰 수부터 차례로 하나씩 뽑기 위해 정렬합니다.

정렬된 값에서 큰 순서대로 k-1 번째까지의 수를 a[n-1]-a[0] 에 모두 빼주면 k개의 조를 나누었을 때의 최소비용을 구할 수 있습니다.

코드

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int n, k;
vector<int> arr;

int main()
{
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    
    cin >> n >> k;
    arr.reserve(n);
    for(int i=0; i<n; ++i)
    {
        int temp;
        cin >> temp;
        arr.push_back(temp);
    }

    vector<int> intervals;
    intervals.reserve(n-1);
    for (int i=1; i<n; ++i)
        intervals.push_back(arr[i] - arr[i-1]);

    sort(intervals.begin(), intervals.end());

    for (int i=0; i<k-1; ++i) // k개의 조를 나누기 위해서 k-1개의 칸막이가 필요하다.
        intervals.pop_back();

    int cost = 0;
    for (int interval : intervals)
        cost += interval;

    cout << cost << endl;
    return 0;
}

너무 직관적으로 풀이를 떠올린것 같아 일부러 최대한 논리적으로 풀이를 작성해보았다.