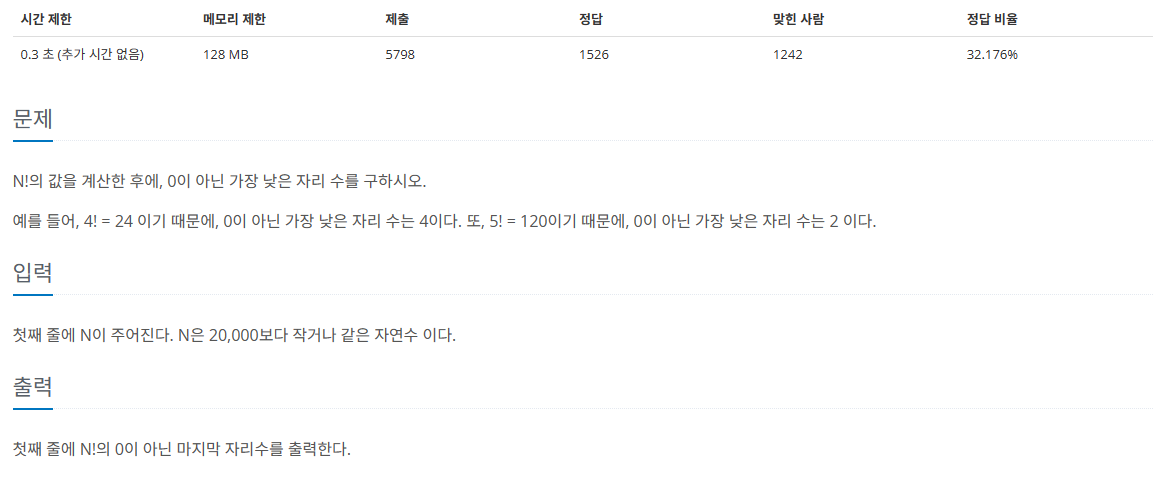
문제

2553번: 마지막 팩토리얼 수

풀이

팩토리얼이 커진다면 2와 5가 계속해서 많이 곱해지기 때문에 가장 낮은 자리 수는 0으로 고정됩니다.
하지만 구해야 하는 수는 0이 아닌 가장 낮은 자리 수 이기 때문에 0을 제거하기 위해 10이 되는 2와 5가 곱해지는 경우들을 제거해야 합니다.

이를 위해, 우선 팩토리얼을 5개씩 끊어서 계산합니다.

그 다음 5의 배수들을 맨 앞으로 넘겨 묶어 줍니다.

5의 배수끼리 묶은 수를 $5^n \times n!$로 표현합니다.

놀랍게도 4개씩 묶은 수들은 모두 곱하면 4로 끝나게 됩니다. 따라서 아래와 같이 식을 변형할 수 있습니다.

10을 날리기 위해 식을 또 변형하면

즉, 5의 배수 팩토리얼의 0이 아닌 가장낮은 자리수는 $n! \times 2^n$ 형태로 나타낼 수 있습니다.
또 2의 제곱수의 가장 낮은 자리수는 2, 4, 8, 6, 2, 4 ,8, 6 ,... 으로 반복되므로

가 최종 공식이 됩니다.

이때 $n$은 입력된 수 / 5 입니다.

그렇다면 5의 배수가 아닌 경우는 어떻게 구해야 할까요?
예를 들어 $17!$ 을 구해야 한다면 간단히 $15! \times 16 \times 17$의 가장 낮은 자리수를 구하면 됩니다. $15!$을 공식으로 간단히 구할 수 있으므로 1의 자리수만을 곱해주면 답을 구할 수 있습니다.

공식을 보면 알겠지만 $n!$을 구하기 위해서는 $(\frac{n}{5})!$을 구해야합니다.
재귀 함수를 사용하여 top-down 방식으로도 구할 수 있고,
반복문을 통해 $1!$부터 $n!$까지 bottom-up 방식으로도 구할 수 있습니다.

코드

Bottom-up

#include <iostream>
#include <cmath>

using namespace std;

int main() 
{
    int N;
    cin >> N;
    
    int dp[20001];
    dp[0] = dp[1] = 1;
    dp[2] = 2;
    dp[3] = 6;
    dp[4] = 4;

    for (int i = 5; i <= N; i++) {
        if (i % 5 == 0) 
        {
            int q = i / 5;
            dp[i] = ((int)pow(2, q % 4) * dp[q]) % 10;
        } 
        else 
        {
            int before = (i / 5) * 5;
            int total = 1;
            for (int j = before+1; j <= i; j++) 
            {
                total *= (j % 10);
            }
            total *= dp[before];
            dp[i] = total % 10;
        }
    }

    cout << dp[N] << endl;
    return 0;
}

Top-down

#include <iostream>
#include <cmath>

using namespace std;

int getQPac(int n)
{
    switch(n)
    {
        case 0:
        case 1:
            return 1;
        case 2:
            return 2;
        case 3:
            return 6;
        case 4:
            return 4;

        default:
            int q= n / 5;
            int qtime5 = q * 5;

            int ret = getQPac(q) * pow(2, q%4);
            for (int i=qtime5+1; i <= n; ++i)
            {
                ret *= i % 10;
            }
            return ret % 10;
    }
}

int main()
{
    int n;
    cin >> n;

    int answer = getQPac(n);

    cout << answer << endl;
    return 0;
}

참고

https://steady-coding.tistory.com/322
https://www.youtube.com/watch?v=RmENut3ZmnM
https://www.campusgate.in/2013/10/finding-right-most-non-zero-digit-of.html