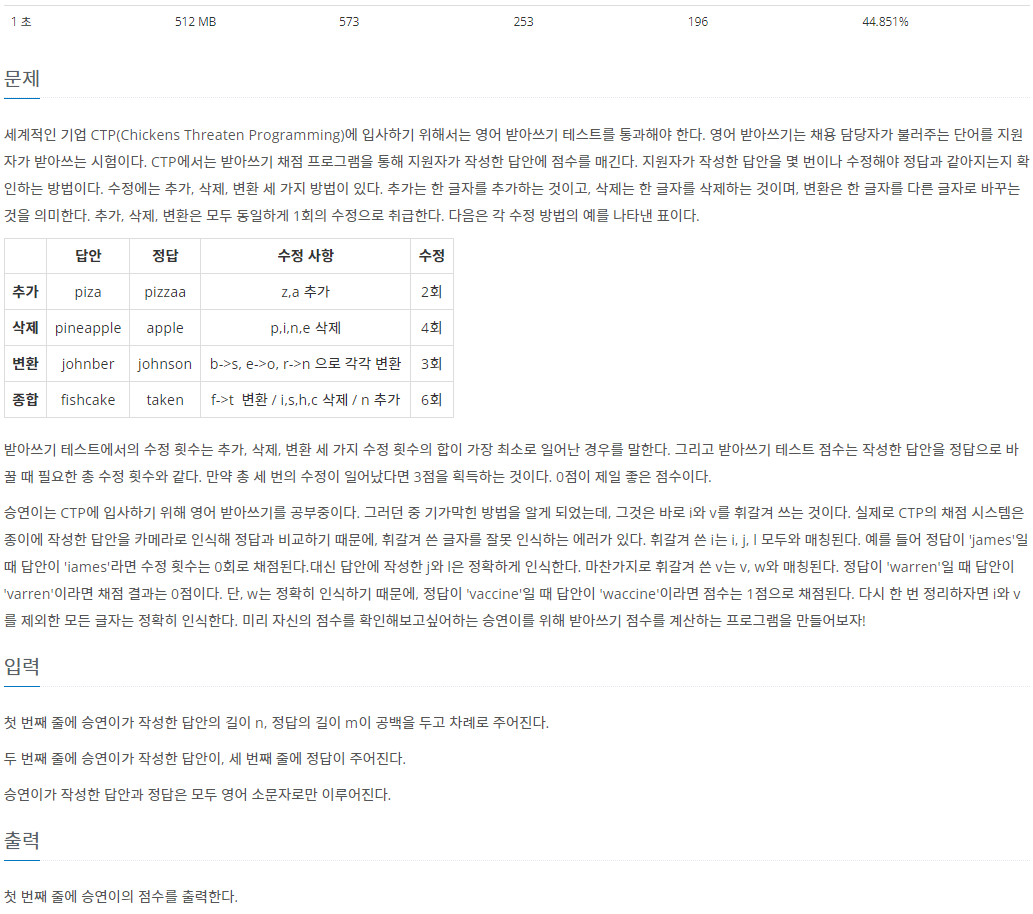
문제

20542번: 받아쓰기

풀이

LCS와 비슷한 편집 거리 알고리즘이라는 방법으로 해결할 수 있다.
제한사항으로 1 ≤ n × m ≤ 10,000,000 이 주어졌기 때문에 $O(n \times m)$으로 해결할 수 있겠다고 생각했다.

dp 테이블의 각 인덱스까지의 수정 개수를 이용해서 다음 인덱스의 수정 개수를 결정하는 문제였다.

또한 제출된 i는 답안의 i, j, l와 비교했을 때 true를 반환해야하고
제출된 v는 v, w와 비교했을 때 true를 반환해야 하기 때문에
알파벳 개수 제곱 크기의 2차원 배열을 만들어 제출답과 답안을 비교할 때 사용하였다.

코드

#include <iostream>
#include <vector>

using namespace std;

int max(int a, int b){ return a > b ? a : b; }
int min(int a, int b){ return a < b ? a : b; }

vector<vector<bool>> spelling(26, vector<bool>(26, false));

bool spellCheck(char submit, char answer){
    int A = submit - 'a';
    int B = answer - 'a';
    return spelling[A][B];
}

int main () {
    cin.tie(0);
    ios_base::sync_with_stdio(false);

    int n, m;
    string submit;
    string answer;
    cin >> n >> m;
    cin >> submit;
    cin >> answer;
    for (char i = 'a'; i <= 'z'; i++){
        int idx = i - 'a';
        spelling[idx][idx] = true;
    }
    spelling['i'-'a']['j'-'a'] = true;
    spelling['i'-'a']['l'-'a'] = true;
    spelling['v'-'a']['w'-'a'] = true;
    
    vector<vector<int>> dp(n+1, vector<int>(m+1));
    for (int i=0; i < n+1; i++){
        dp[i][0] = i;
    }
    for (int i=0; i < m+1; i++){
        dp[0][i] = i;
    }

    for (int i=1; i<n+1; i++){
        for (int j=1; j<m+1; j++){
            if (spellCheck(submit[i-1], answer[j-1])){
                dp[i][j] = dp[i-1][j-1];
            }
            else{
                int temp = min(dp[i-1][j], dp[i][j-1]);
                dp[i][j] = min(dp[i-1][j-1], temp) +1;
            }
        }
    }

    cout << dp[n][m] << endl;

    return 0;
}