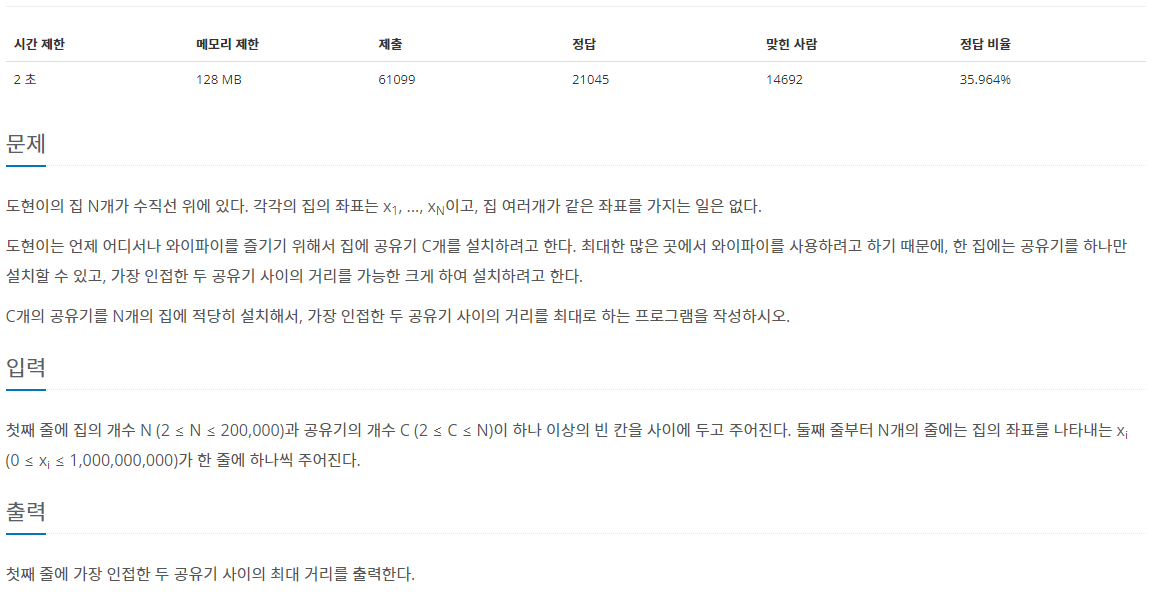
문제

2110번: 공유기 설치

풀이

프로그래머스의 징검다리 문제와 비슷한 문제이다. 이 문제도 이분 탐색을 이용하여 가장 인접한 공유기 사이의 거리가 최대가 되도록하는 문제다.

이분 탐색으로 해결하기 위해 탐색할 x를 공유기 사이의 거리로 두고, f(x)를 인접한 공유기 사이의 모든 거리가 x보다 클때의 최대 공유기 수로 두었다. x가 커질 수록 f(x)는 작아지는 감소함수 형태이다.
이때 공유기가 최대한 많아야 하기 때문에 가장 첫번째 위치의 집에 무조건 공유기를 두도록 했다.
그 후 첫 번째 집에서 x 보다 멀리 떨어진 집을 발견하면 공유기를 설치하고 또 그 뒤로 x보다 먼 집이 발견되면 공유기를 설치하며 최대 공유기 수를 계산하였다.

int calRouter(int minDist){
    int routerCnt = 1; // coordinates[0]집은 무조건 무조건 공유기 설치
    int curLoc = coordinates[0];
    for (int i=1; i < n; i++){
        int nextLoc = coordinates[i];
        if (nextLoc - curLoc >= minDist){
            routerCnt++;
            curLoc = nextLoc;
        }
    }
    return routerCnt;
}

하지만 항상 공유기 수가calRouter(x)일때 가장 인접한 공유기 사이의 거리가 x라는 보장은 없다. calRouter(x)는 공유기 사이의 거리가 x보다 클때 이므로 항상 x와 일치하는 것이 아니고, 가장 인접한 공유기 사이의 거리가 x보다 큰 경우도 발생하게 된다.
따라서 calRouter(x) = a중에서 가장 인접한 공유기 사이의 거리가 x와 일치하게 되는 경우는 calRouter(x) = a인 x 들 중에서 x가 가장 큰 수일때를 찾으면 된다.
그러므로 calRouter(x) >= 공유기 수 일때의 x의 최대값을 이분탐색으로 찾으면 된다.

코드

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int n, c;
vector<int> coordinates;

int calRouter(int minDist){
    int routerCnt = 1; // coordinates[0]집은 무조건 무조건 공유기 설치
    int curLoc = coordinates[0];
    for (int i=1; i < n; i++){
        int nextLoc = coordinates[i];
        if (nextLoc - curLoc >= minDist){
            routerCnt++;
            curLoc = nextLoc;
        }
    }
    return routerCnt;
}

bool check(int mid){
    int router = calRouter(mid);
    return router >= c;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);

    cin >> n >> c;
    for (int i=0; i < n; i++){
        int loc;
        cin >> loc;
        coordinates.push_back(loc);
    }
    sort(coordinates.begin(), coordinates.end());

    int lo = 1;
    int hi = coordinates[n-1]+1;

    while (lo <= hi){
        int mid = (lo + hi) / 2;
        if (check(mid)){
            lo = mid + 1;
        }
        else {
            hi = mid - 1;
        }
    }

    int target = hi;

    cout << target << endl;

    return 0;
}

/*
mid 는 공유기 간의 최소 거리
calRouter(mid)는 각 공유기 사이의 거리가 mid 이상일 때의 공유기 수
*/