문제

1823번: 수확

풀이

수확한 벼의 개수에 따라 생기는 밭의 모양마다의 최대값을 이전 밭의 상태일때의 최대값을 이용하여 구하며 모든 벼를 수확했을 때의 최대값을 구하는 DP 문제이다.

똑같은 n개의 벼를 수학해도 왼쪽, 오른쪽 수확한 벼의 개수가 다른 경우 밭은 다른 상태를 갖게 된다.
이러한 다른 상태들의 밭을 정의하기 위해 2차원 배열을 사용한다.
dp[left][right]는 밭의 벼를 왼쪽에서left번째 까지, 오른쪽에서right번째 까지 수확한 상태임을 나타낸다.

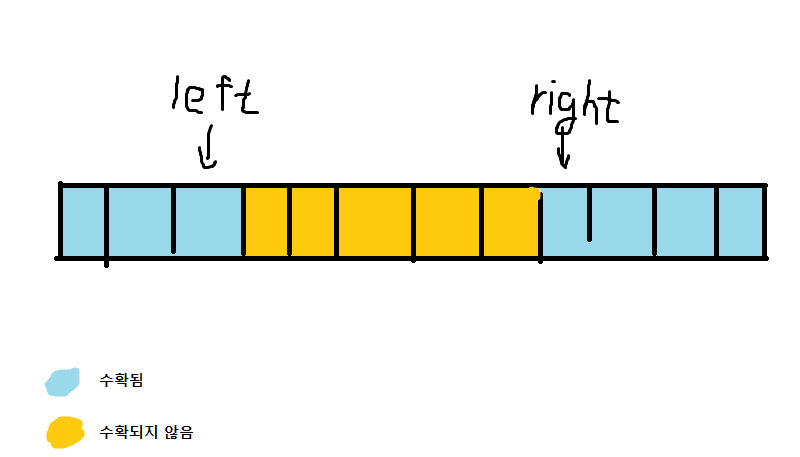
dp[left][right]의 값은 같은 상태 중에서 최대값을 가져야 한다. 이를 정의하기 위해 이전상태(각 왼,오른쪽에서 하나씩 덜 수확한 상태)값 + 수확한 벼의 개수 * 벼의 값어치 중 더 큰 값을 선택한다.
이를 코드로 나타내면

dp[i][j] = max( dp[i-1][j] + rices[i] * cnt, dp[i][j+1] + rices[j] * cnt );

완성된 2차원 배열에서 dp[i][i+1]에 해당하는 부분은 수확이 모두 완료된 상태이므로 그 중 최대값을 선택해 출력하면된다.

코드

#include <iostream>
#include <vector>

using namespace std;

int max(int a, int b){
    if (a > b) return a;
    else return b;
}

int main () {
    int n;
    cin >> n;
    vector<int> rices(n+2, 0); 
    for (int i=1; i<n+1; i++){ // 1 ~ n+1
        cin >> rices[i]; // 0, input... , 0
    }
    vector<vector<int>> dp(n+2, vector<int>(n+2, 0)); // dp[left][right] => rices에서 left, right까지 수확을 완료한 상태
    dp[0][n+1] = 0; // 초기 값
    for (int i=1; i < n+1; i++){
        int cnt = i;
        dp[i][n+1] = dp[i-1][n+1] + rices[i] * cnt;
    }
    for (int j=n; j > 0; j--){
        int cnt = n+1 - j;
        dp[0][j] = dp[0][j+1] + rices[j] * cnt;
    }

    for (int i=1; i<n+2; i++){
        for (int j=n; j>i; j--){
            int cnt = (i - 0) + (n+1 - j);
            dp[i][j] = max( dp[i-1][j] + rices[i] * cnt, dp[i][j+1] + rices[j] * cnt );
        }
    }
    
    int answer=0;
    for (int i=0; i < n+1; i++){
        answer = max(answer, dp[i][i+1]);
    }

    cout << answer << endl;
    // for (auto i: dp){
    //     for (auto j: i){
    //         cout << j << "\t";
    //     }cout << endl;
    // }

    return 0;
}