Symbol Table
created : 2023-12-13
What I Learned
Symbol Table 이란 ?
Key와 Value 쌍을 저장하는 데이터 구조, 특히 Key를 검색어로 주었을 때, 대응되는 value를 빠르게 찾아주는 구조
Ex)
| Domain Name | IP Address |
| (Key) | (Value) |
| www.knu.ac.kr | 155.230.11.1 |
| computer.knu.ac.kr | 155.230.13.8 |
특징
- 사용하는 key가 unique해야 한다.
Symbol Table 구현하는 방법
-
Unordered List 사용
LinkedList 또는 배열에 원소를 정렬하지 않고 저장하는 방식- Get(key) : 주어진 key가 symbol table에 있는지 찾아본 후, 있으면 Value를 반환하고 없으면 예외 혹은 None을 반환한다.
정렬되지 않은 상태이므로 수행하는데 O(N) 에 비례한 시간이 걸린다.- Put(key) : 주어진 key가 symbol table에 있는지 찾아본 후, 존재한다면 기존의 value를 새 값으로 덮어쓰고, 없으면 새로운 (key,value) 쌍을 추가한다.
따라서, 먼저 Get을 수행하고, 대체 혹은 삽입 작업을 수행한다. 마찬가지로 O(N) 에 비례한 시간이 걸린다.
- Put(key) : 주어진 key가 symbol table에 있는지 찾아본 후, 존재한다면 기존의 value를 새 값으로 덮어쓰고, 없으면 새로운 (key,value) 쌍을 추가한다.
- Get(key) : 주어진 key가 symbol table에 있는지 찾아본 후, 있으면 Value를 반환하고 없으면 예외 혹은 None을 반환한다.
-
Ordered Array 사용
원소를 정렬한 상태로 배열에 저장하는 방식.
정렬을 위해서 각 원소의 index가 필요 -> 배열에 저장- Get(key) : 데이터가 정렬되어 있는 상태이기 때문에 이진 탐색을 사용하여 데이터를 조회한다.
따라서, O(logN) 에 비례한 시간이 걸린다. - Put(key) : get()을 사용해 해당 key를 조회한 후, 새로운 값을 덮어쓰거나 추가한다.
이때, 새로운 (key, value)쌍을 추가한다면 추가한 원소의 뒤에 위치한 원소들을 한 칸씩 뒤로 옮겨야한다. 따라서, O(N) 에 비례한 시간이 걸린다.
- Get(key) : 데이터가 정렬되어 있는 상태이기 때문에 이진 탐색을 사용하여 데이터를 조회한다.
-
BST(Binary Search Tree) 사용
트리의 각 노드에 하나의 (Key, Value) 쌍 저장
자식이 0 ~ 2 개, 왼쪽 자식 key < 부모 key < 오른쪽 자식 key 를 만족하는 트리- Get(key) : 데이터가 이진트리형태로 저장되어 있으며 이진 탐색을 통해 최대 깊이 N(Worst Case)까지 조회한다. 따라서, O(N) 에 비례한 시간이 걸린다.
- Put(key) : Get을 통해 key에 대한 조회를 하고 새 노드를 추가하거나 덮어쓰는 작업을 수행한다. 이때 작업에 걸리는 시간은 상수 시간이 걸린다. 따라서 O(N) 에 비례한 시간이 걸린다.
- 트리의 양쪽이 완전히 균형 잡힌 상태가 된 경우 깊이 : logN
- 트리가 한쪽으로만 깊어져 모든 원소가 일렬로 늘어선 경우 깊이 : N
-
Hash 값 사용
hash 함수 h(key) 계산한 값을 index로 사용해 hash table의 저장할 위치에 바로 접근 (상수 시간)- Get(key) : key의 해쉬 값을 계산하여 데이터에 상수시간에 접근할 수 있다.
- Put(Key) : get()을 통해 데이터에 바로 접근할 수 있고 수정에도 상수시간이 걸린다.
데이터에 hash 함수를 적용시켜 서로 떨어뜨려놓기 위한 목적으로 사용
key와 근접한 값 탐색이나, 원소 순서 파악에는 불리하다.
BST 방식의 Symbol Table 성능 향상
[2-3 Tree]
각 노드에 2개까지의 Key 저장을 허용 & 3개까지의 자식 허용 (트리 깊이를 최소화하기 위함)
2 - node -> 1 개의 key, 2 개의 자식 가진 노드 (BST와 동작 방식 같음)
3 - node -> 2 개의 key, 3 개의 자식 가진 노드
- key < k1 : 왼쪽 자식으로 이동
- k1 < key < k2 : 가운데 자식으로 이동
- k2 < key : 오른쪽 자식으로 이동
2-3 Tree 방식으로 Symbol Table 을 구현한다.
Put 메서드에 대해서 노드 타입에 따라 다음과 같이 수행한다.
- get(key)를 통해 찾은 노드가 2-Node : 2-Node를 3-Node를 만든다.
- get(key)를 통해 찾은 노드가 3-Node :
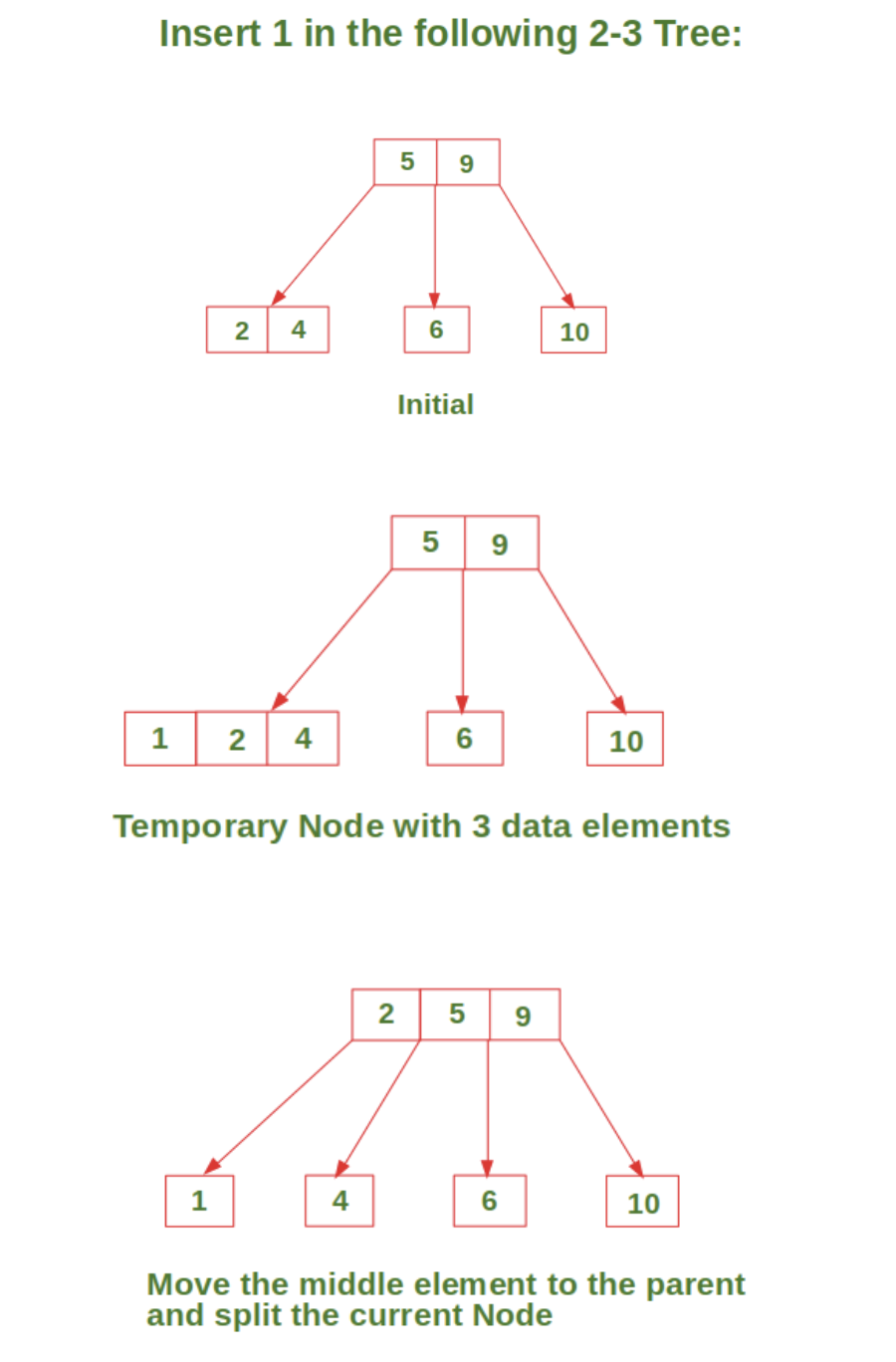
임시로 4-Node를 만든 후 가운데 key를 부모 노드에 추가하며 2개의 2-Node를 만든다.
부모노드가 4-Node가 된다면 중간 노드를 새로운 Root로 만들면서 트리깊이를 1 증가시킨다.
성능이 어떻게 향상되는가 ?
한쪽으로 노드가 몰리게되면 (4-Node) 해당 노드가 Split하면서 양쪽이 균형잡힌 트리로 분화하게 된다.
root ~ leaf 노드 까지 모든 경로가 같은 길이를 유지한다.
따라서, 깊이가 ~logN을 보장하게 된다.
대부분의 작업이 O(logN)에 비례하게 된다.
구현이 어려운 문제점...
트리를 순회하며 만나는 노드의 타입이 2-node, 3-node, 4-node가 있고 구분하여 처리할 필요가 있다.
3-node 따라 탐색해 내려갈 때는 대소 비교 여러 회 필요
Leaf에 새 값 추가 후 root로 거슬러 올라가며 4-node split 필요
4-node split할 때 여러 링크를 정확한 위치에 바꾸어 연결해 주어야 하는 등의 구현적 어려움이 있다.
BST 코드 재활용/변형을 통한 2-3 Tree 구현방법
[LLRB] Left-Leaning Red-Balck
내부 연결(Red)과 외부 연결(Black) 구분하여 표현하는 방식
내부 연결은 왼쪽으로 기울어지도록 표현 -> 작은 값을 큰 값 왼쪽에 둔다.
- 2-node : BST 그대로 사용
- 3-node : 2개의 2-node를 내부연결하여 표현, 즉 원래 한 노드에 놓여있던 2개의 key 중 작은 key를 부모로 하는 2-node를 만든 후 큰 key와 내부연결(Red Edge)로 연결해준다.
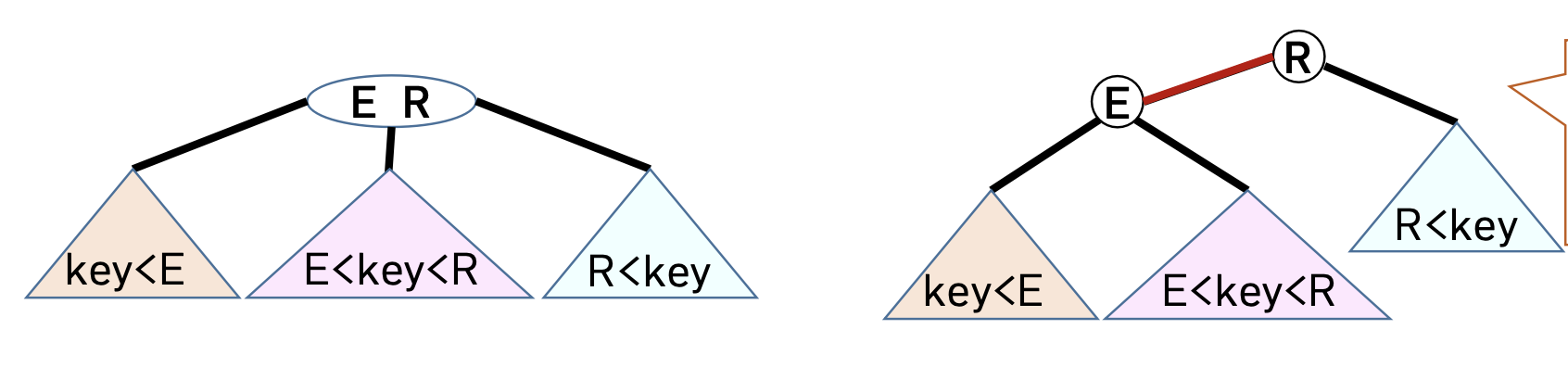
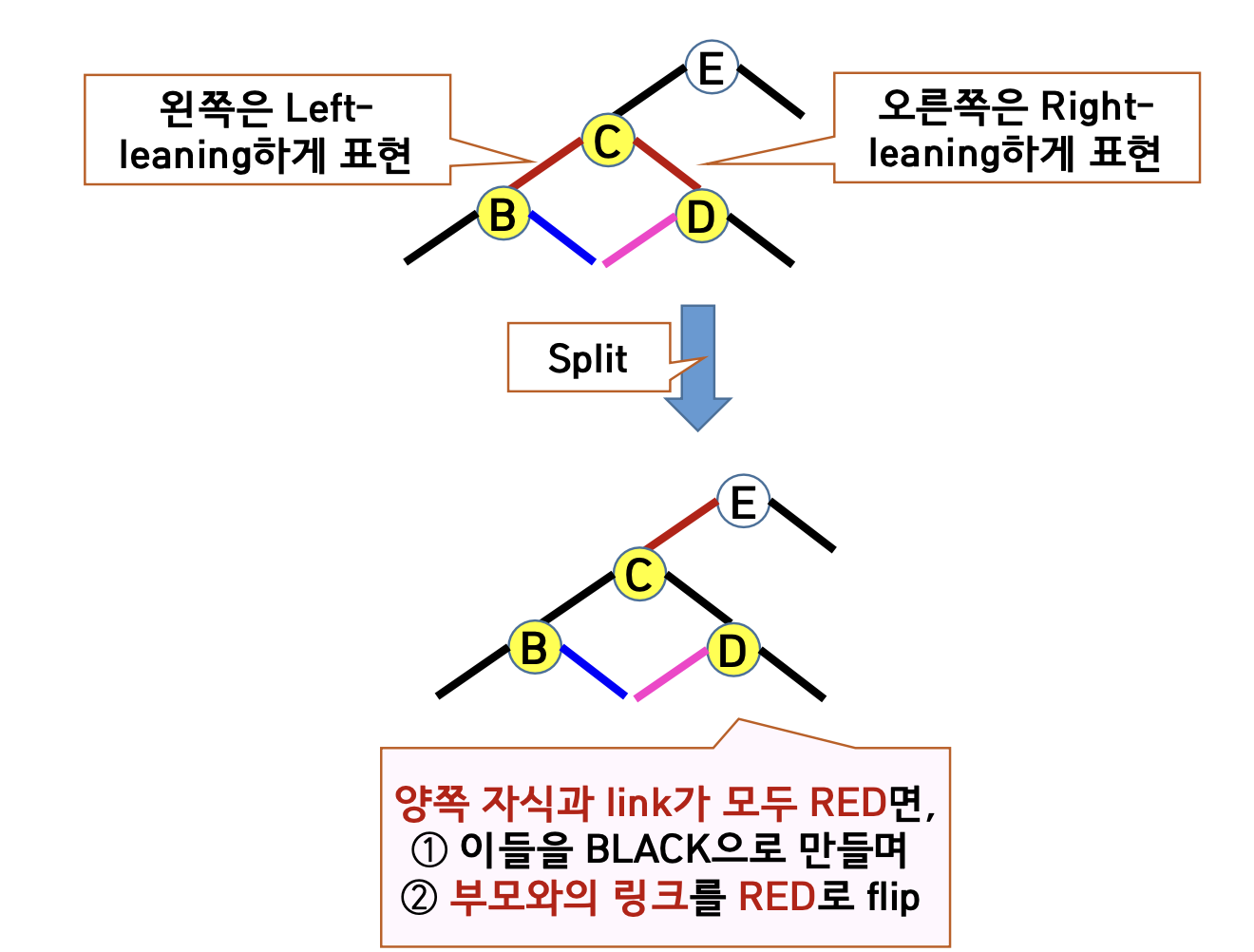
- 4-node : 양쪽 자식이 모두 내부 연결 된 경우 이들을 외부 연결 로 만든 후 부모와의 연결을 내부 연결 로 바꾸어준다.
BST를 활용한 2-3 Tree에서의 작업
- Get() : 링크의 색깔을 고려하지 않고 BST에서의 탐색방식 그대로 탐색 가능
- Put() :
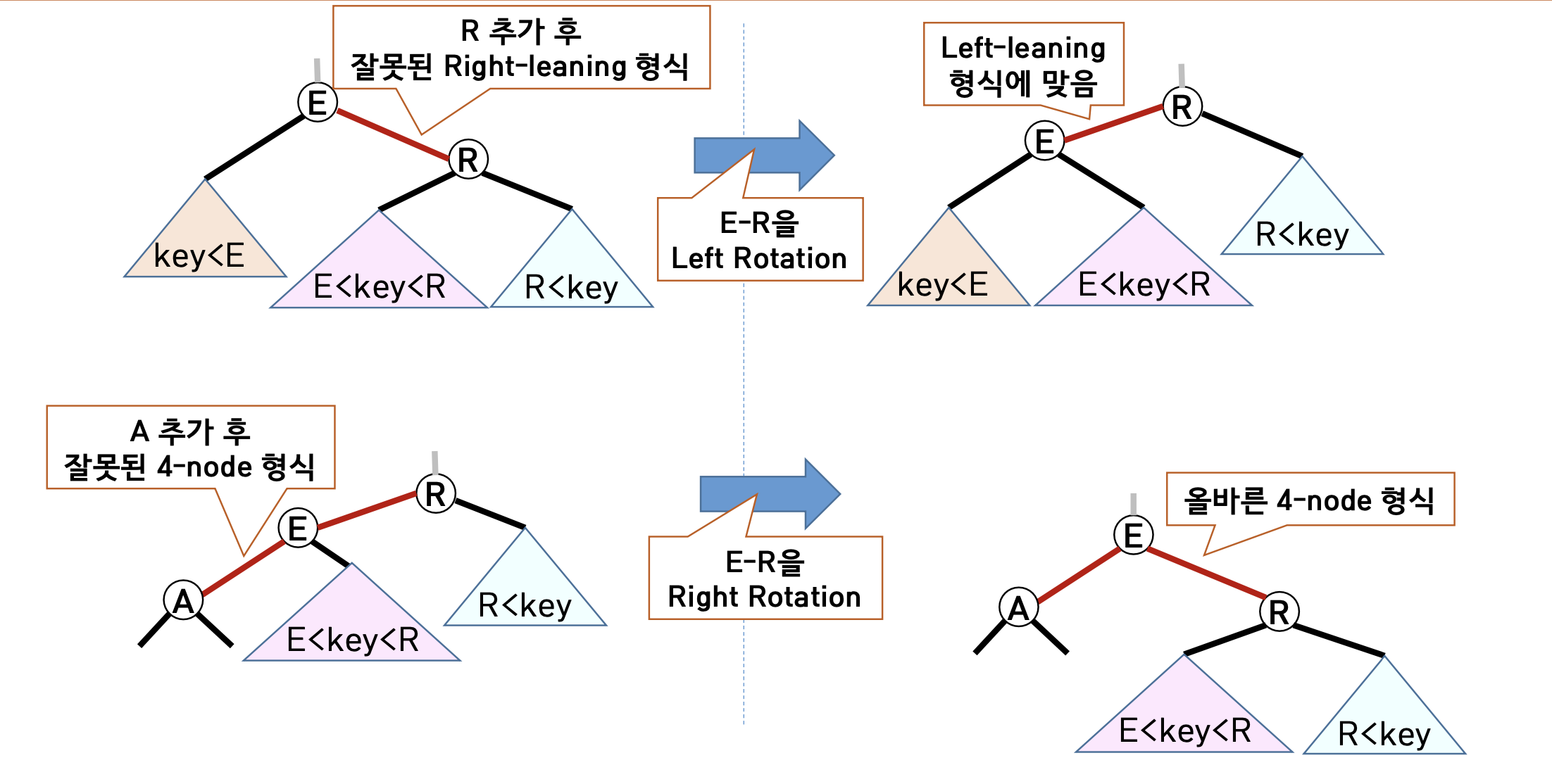
- 모든 추가되는 노드의 LINK는 RED이다.
- 노드의 오른쪽 LINK가 RED 이고 왼쪽 LINK가 BLACK인 경우 leftRotate 시켜준다.
- 노드의 양쪽링크가 RED인 경우 rightRotate 시켜준다.
- 양쪽 링크가 RED 인 경우 양쪽 링크를 BLACK로 변경시키고 부모와의 링크를 RED로 변경시켜준다.
- root와의 링크는 항상 BLACK이다.
Summary
핵심 1.
Symbol Table 이란 key와 Value 쌍을 저장하는 데이터 구조이다.
Key를 활용해 해당 key를 가지는 데이터를 조회하는 기능을 제공한다.
핵심 2.
Symbol Table 을 구현하는 방법은
- Unordered List (정렬하지 않은 리스트 혹은 배열)
- 정렬된 배열
- 이진트리
- 해쉬 값을 활용한 테이블
이 있다.
핵심 3.
정렬되지 않은 List의 조회 기능은 O(N)에 비례한다
정렬된 List의 조회 기능은 이진탐색을 활용할 수 있어 O(logN)에 비례하지만, 삽입 시 원소의 순서를 유지하기 위해 O(N)에 비례한 시간이 걸리는 단점이 있다.
이진트리의 조회 기능은 트리의 깊이에 비례한다. 다만 편향된 트리가 생길 수 있으며 이때 깊이가 N이 될 수 있다.
해쉬함수를 활용한 테이블의 조회 및 삽입 기능은 상수시간에 수행된다. 다만 key와 근접한 값 탐색 혹은 원소 순서 파악 등에는 불리하다.
핵심 4.
이진트리를 개선한 방식으로 2-3 Tree 를 이용하여 Table을 구현할 수 있다.
2-3 Tree를 활용하면 트리의 깊이가 logN 으로 유지시킬 수 있어 값 조회 기능의 성능을 향상 시킬 수 있다.
깊이 유지가 되는 이유는 4-node 가 되는 경우 split하여 균형잡힌 트리로 분리되기 때문
핵심 5.
2-3 Tree 를 구현하기 위해 기존의 BST 트리를 구현한 코드 재활용할 수 있다.
이것이 LLRB(Left Leaning Red Black)이다.
