알고리즘 - Graph

ChansooJeong·2023년 12월 14일

BFS DFS TopologicalSort 그래프 알고리즘 위상정렬 코사라주알고리즘

알고리즘

목록 보기

2/4

Undirected and Directed Graph

created : 2023-12-14

What I Learned

Graph 란?

정점과 이들을 연결하는 간선으로 이루어진 데이터 구조.
지도 혹은 인터넷과 같은 물리적인 연결 관계를 나타내기도 하지만, 그 외 다양한 추상적인 연관성을 나타내기 위해서도 사용된다.
이러한 그래프 중 간선에 방향성이 있는 그래프를 방향 그래프 , 방향성이 없는 그래프를 undirected Graph라고 한다.

그래프를 저장하는 방식

그래프에서 가장 많이 필요로 하는 기능 ?
-> 정점 V 에 인접한 모든 정점의 목록을 얻는 기능

adjacency-list 방식
길이가 정점 개수 V 인 배열(adj [])을 두고 adj[v]에는 v와 인접한 정점의 리스트를 저장하는 방식
각 리스트에 저장된 정점은 정렬될 필요 없다.
각 정점에 인접한 정점의 목록을 얻는 작업을 수행할 때 상수 시간만 소요된다.
adjacency-matrix 방식
V * V 크기의 2차원 배열을 만들어 adj(v)(w)에 정점 v와 w를 연결하는 간선의 수를 저장하는 방식
정점 V에 인접한 모든 정점의 목록을 얻기위해 adj[v]행의 모든 열을 하나씩 검사해야한다. 따라서 V에 비례한 시간이 소요된다.

그래프를 탐색하는 방식

그래프 탐색이란, 정점 s가 출발지로 주어졌을 때 이로부터 도달 가능한 곳과 경로를 찾는 것
탐색이 필요한 이유

그래프 내의 특정 목표 찾기
목적지까지 경로가 있음을 보이기
목적지까지 임의의 경로 혹은 최단 경로 찾기
그래프의 전반적인 연결 상태를 알아내 이후에 활용하기

DFS(Depth-First Search)

DFS(V) :
	visit[V] = true
	adjacent_list = adj[V]
	for v in adjacent_list :
		if not visit[v] : DFS(v)

탐색을 시작할 정점 s가 주어졌을 때, s로부터 도달 가능한 모든 정점을 방문해 보며 어느 곳이 도달 가능한지를 기록하는 것. (도달할 수 있는 곳까지 최대한 깊이 탐색하는 형태)
이 과정에서 거쳐온 경로도 기록
두 정점 간에 경로가 있는지 확인하고 -> 있다면 그 중 하나의 경로를 찾는 방법

s로부터 도달 가능한 정점과 간선 수가 V와 E라고 할 때, DFS의 수행시간은 O(V+E)에 비례한다.

BFS(Breadth-First Search)

BFS(V) :
	queue.put(s)
	visit[s] = true
	
	while not queue.isEmpty() :
		cur_vertex = queue.get()
		
		for v in adj[cur_vertex] :
			if not visit[v] :
				visit[v] = true
				queue.put(v)

탐색을 시작할 정점 s가 주어졌을 때, s로부터 도달 가능한 모든 정점을 방문해 보며 어느 곳이 도달 가능한지를 기록하는 것. (한 번에 갈 수 있는 여러 갈래길을 동시에 넓게 탐색하는 형태)

s로부터 도달 가능한 정점과 간선 수가 V와 E라고 할 때, BFS의 수행시간은 O(V+E)에 비례한다.
모든 정점을 한 번씩 방문하게 된다 (~V)
방문한 정점에 인접한 간선에 대해 하나씩 차례로 그 간선의 방문 여부를 확인한다 (~E)

BFS와 DFS를 활용한 예 - Connected Component

그래프가 주어졌을 때, 서로 간에 모두 연결된 정점의 최대 집합을 찾는 문제.
Union-Find와 비슷해 보일 수 있지만, 차이점이 있다.

그래프의 연결 상태가 바뀔 수 있는가
- YES => Union-Find
- NO => DFS 와 BFS

Connected_Component :
	for v in all_vertex :
		if not visit[v] : 
			BFS(v, componentIdx) or DFS(v, componentIdx)
			# 방문한 모든 정점 w를 v와 같은 component에 속하는 것으로 기록한다(componentIdx).

BFS와 DFS를 활용한 예 - Garbage Collection

프로그램의 control-flow를 분석해서 그래프로 표현이 가능하다.

정점 : 명령어
간선 : 실행 순서
Cycle 을 이룬다면 무한 loop 발생 가능
특정 영역으로 도달하는 간선이 없다면 도달 불가능함을 작성자에게 알리는 등

[Garbage-Collection] : 사용하지 않는 객체 메모리 제거
동적으로 메모리 할당한 객체들은 그래프로 표현이 가능하다.
정점 -> 객체
간선 -> 참조 관계
주기적으로 root를 시작점으로 객체 간 참조관계를 확인하며 도달 불가능한 정점(객체)를 찾는다.
도달 불가능한 정점이 발견되면 더는 프로그램에서 사용하지 않는 것으로 해석하고 메모리에서 삭제한다.

Topological Sort (위상 정렬)

간선 향하는 방향 순으로 정점의 순서를 정하는 정렬 방식
Topological Order : v -> w 향하는 간선이 존재한다면, 정점 간 순서는 v 후에 w 가 오도록 하는 순서
활용 : 여러 작업 간 선후 관계 있을 때, 이를 따르도록 수행하는 순서 정하기 등
그래프에 Cycle이 없어야 Topological Order를 가질 수 있다. (순환적 관계)

Topological Order를 얻는 방법 ?

물이 흘러가는 순서 VS 물이 차오르는 순서
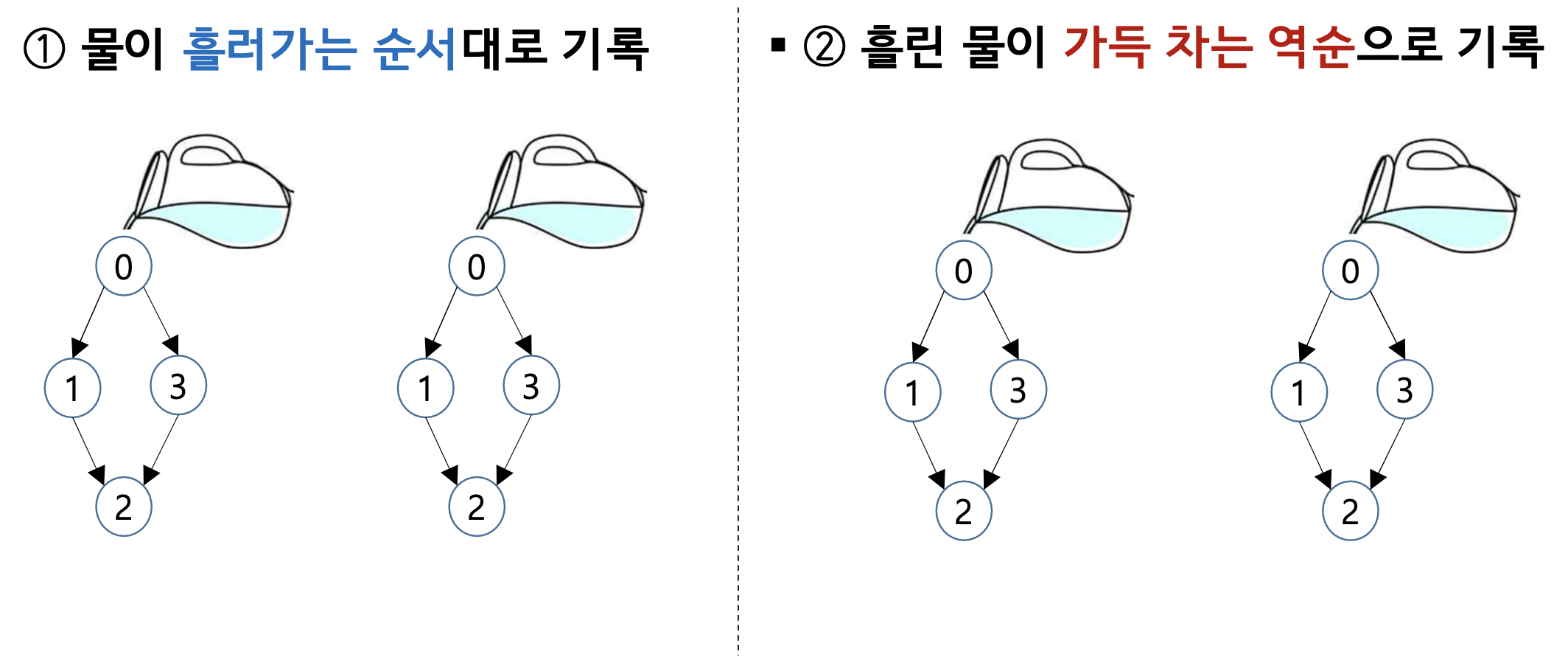
흘러가는 순서 : 0 -> 1 -> 2 -> 3 / 0 -> 3 -> 2 -> 1 => Topological Order를 따르지 않는다 !
차오르는 순서 : 2 -> 1 -> 3 -> 0 / 2 -> 3 -> 1 -> 0 => 역순이 Topological Order를 따른다 !

DFS의 탐색 방법을 활용하여 Topological Order 를 구할 수 있다.
가장 깊이 탐색한 후 -> 반환해서 돌아 나올 때, 정점 v를 역순으로 기록한다.

DFS(v) :
	visit[v] = true
	for e in adj[v] :
		if not visit[e.w] : 
			DFS(e.w)
	topological_Order.prepend(v)

물을 흘려 보내는 지점을 정하는 방법
모든 지점에서 순서를 고려하지 않고 DFS로 탐색하면 된다 !
혹은
Indegree 가 0인 지점을 Queue에 추가하며 BFS로 탐색하되, 방문한 지점의 Indegree를 -1씩 감소시켜주면서 진행하는 방법도 있다.
Topological Sort 수행 시간
- 모든 정점을 방문한다 => V
- 모든 OutDegree를 확인한다 => E
- ~ O(V+E) 에 비례한 수행시간

Topological Sort 를 활용한 예 - Strongly Connected Component

Strongly Connected Component -> 양방향으로 도달 가능한 정점의 최대 집합
특징

같은 컴포넌트 내부에 반드시 Cycle이 존재한다.
서로 다른 컴포넌트 간에는 간선이 없거나, 한 방향으로만 존재한다.

서로다른 컴포넌트 간 간선이 없다면
한 컴포넌트 내 어느 정점에서 DFS 혹은 BFS를 시작하더라도, 컴포넌트 내부의 모든 정점을 찾을 수 있다.

서로다른 컴포넌트 간 간선이 존재한다면
각 SCC를 하나의 큰 정점으로 생각하면 Cycle이 존재하지 않는 그래프가 되고, Topological Order를 얻을 수 있다.
얻은 Topological Order의 역순으로 DFS를 적용하면 각 컴포넌트를 찾을 수 있다.

각 컴포넌트를 하나의 정점으로 본 그래프에서 Topological Order의 역순을 찾는 방법 ?
reverse Graph 에 DFS 적용

> 원래 그래프의 topological Order 를 찾아 역순으로 찾을수는 없을까 ?
> 안된다.
> 하위 컴포넌트의 모든 정점보다 상위 컴포넌트의 일부 정점이 먼저 기록되는 경우 발생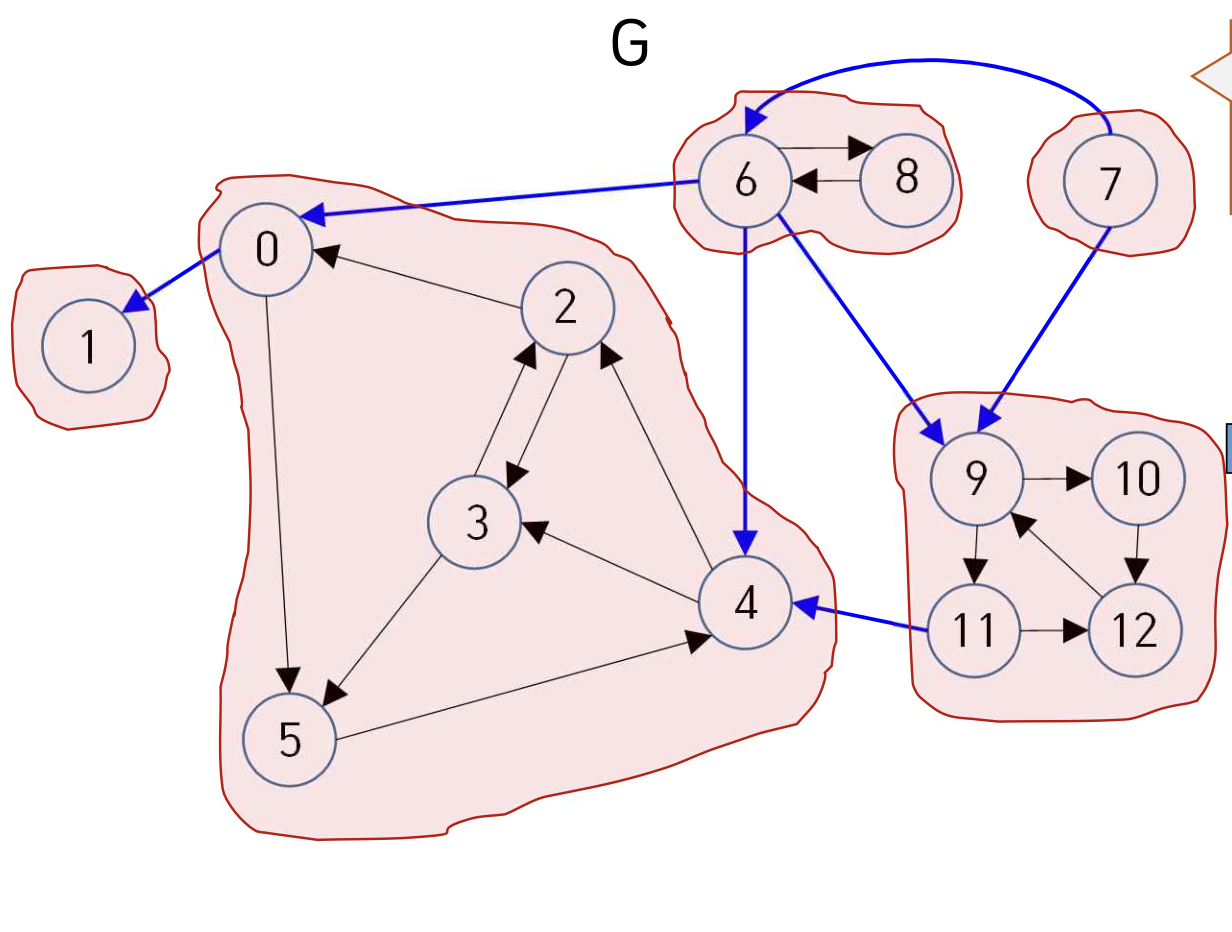

서로 다른 컴포넌트 간의 순서가 중요하다. 
역 그래프에 대해서 Topological Order를 얻으면 최소한 각 컴포넌트에 속한 정점 간 순서가 큰 컴포넌트로 봤을 때의 Topological Order에 맞게끔 나온다.
같은 컴포넌트 내부의 순서는 상관이 없다.

[Kosaraju-Sharir] (코사라쥬-샤이르]알고리즘
1. reverse graph의 topological order 얻기
2. 그 순서로 원래 그래프에 DFS를 수행하여 SCC 찾기
시간복잡도 측정 :
Phase 1 -> DFS 수행시간 -> O(V+E)
Phase 2 -> DFS 수행시간 -> O(V+E)
~ O(V+E)에 비례한 시간이 걸린다.
Phase 2 단계에서 DFS가 아닌 BFS로 수행해도 SCC를 찾을 수 있다

Summary

핵심 1.
그래프는 정점과 간선으로 이루어진 데이터 구조이다.
이를 표현하는 방식으로 인접 리스트, 인접 행렬를 사용할 수 있는데 인접 리스트로 구현할 때 compact하게 구현할 수 있다.

핵심 2.
그래프를 탐색하는 방식으로 BFS, DFS 를 사용할 수 있다.
수행시간은 모두 O(V+E)에 비례한 시간이 걸린다.
이 탐색방법을 활용하여 Connected Component를 찾을 수 있다.

핵심 3.
위상 정렬은 정점 v,w 가 간선 v->w에 의해 연결되어 있을 때, v->w 순서로 정렬하는 것을 말한다.
Topological Order를 찾기 위해 DFS를 이용한다. 이때 시작점으로 Indegree가 0인 정점을 선택한다.

핵심 4.
Strongly Connected Component를 찾기 위해 Topological Order를 이용한다.
이때, 각 컴포넌트를 한 정점으로 본 그래프의 역방향 그래프 Topological Order를 이용한다.
이를 찾기 위해 그래프의 역방향 그래프를 생성하여 Topological Order를 얻는다.
이후 그 순서대로 원래 그래프에 DFS를 수행하여 SCC를 찾을 수 있다.
이 알고리즘을 코사라주-알고리즘이라 칭한다.