WordNet, Outcast 탐지 및 SCA/SAP 찾기
created : 2023-12-14
What I Learned
Set 이란 ?
Symbol Table 에서 value는 제거하고 key만 저장하는 구조
Key의 존재 여부만 빠르게 확인하는 역할
- 특징
- 원소를 추가한 순서를 그대로 보존하는 자료구조가 아니다.
- 임의의 순서로 재배치 될 수 있다.
WordNet 이란 ?
단어 간 의미 관계를 나타내는 Graph
정점 -> 유사어의 집합
간선 -> 의미상 포함 관계 Ex) apple -> edible fruit
사용되는 곳 : 문장 의미 자동 분석, 논리적 추론 등에 사용
Ex) horse zebra cat bear table 중 가장 관련 적은 것은 ?
- 특징
- 싸이클이 존재하지 않는다.
- 부모가 둘 이상인 경우도 있고, 자식이 둘 이상인 경우도 있다.
- Root 는 하나이다. (Entity)
- 같은 단어가 여러 다른 정점에 나타나기도 한다.
Ex) cat (고양이 의미), cat(고양이 과 의미)
Outcast
-
의미 : 단어 집합에서 다른 단어와 가장 의미가 다른 단어
Ex) horse zebra cat bear table 중 Outcast -> table -
탐지방법
두 단어 wi 와 wj의 의미가 다르다 -> WordNet에서 멀리 떨어져 있다.
distance(wi, wj) -> 두 단어 wi 와 wj 간의 의미상 거리 : 가장 가까운 공통 조상까지의 간선 수의 합
단어 집합이 {w1, w2, w3, ... , wn} 이라고 할 때
wi의 거리 합 di = distance(wi, w1) + distance(wi, w2) + distance(wi, w3) + ... + distance(wi, wn)
di가 가장 큰 단어를 Outcast로 선정한다. -
distance 계산 방법
같은 정점에서 만날때까지 wi, wj 각각에서 간선 따라 올라간 후, 거쳐온 간선 수 더함
wi, wj에서 동시 출발
고려해야할 사항 💭
같은 단어 wb, wb에 대해
공통 조상과 조상까지의 경로는 둘 이상일 수 있다.
부모 둘 이상일 수 있다.
이 중 가장 가까운 조상까지 거리를 distance로 사용한다.
SCA, SAP
- SCA (Shortest Common Ancestor) : 두 탐색이 만나는 가장 가까운 정점
- SAP (Shortest Ancestral Path) : wa, wb에서 SCA까지 거쳐온 경로
Outcast({w1, w2, ... , wn}) :
for wi in w집합 :
di = 0
for k in range (1 to n) :
if wi is not wk : di += distance(wi, wk)
return di 가장 큰 단어distance(wa, wb) :
wa, wb에서 출발해 가장 가까운 SCA와 SPA 찾아 경로 길이 반환wa에서 BFS를 수행해 도착할 수 있는 곳과 거리를 표기
wb에서 BFS를 수행해 도착할 수 있는 곳과 거리를 표기
wa와 wb 모두에서 도착할 수 있는 곳 중 합산 거리가 최소인 곳을 SCA로 선정
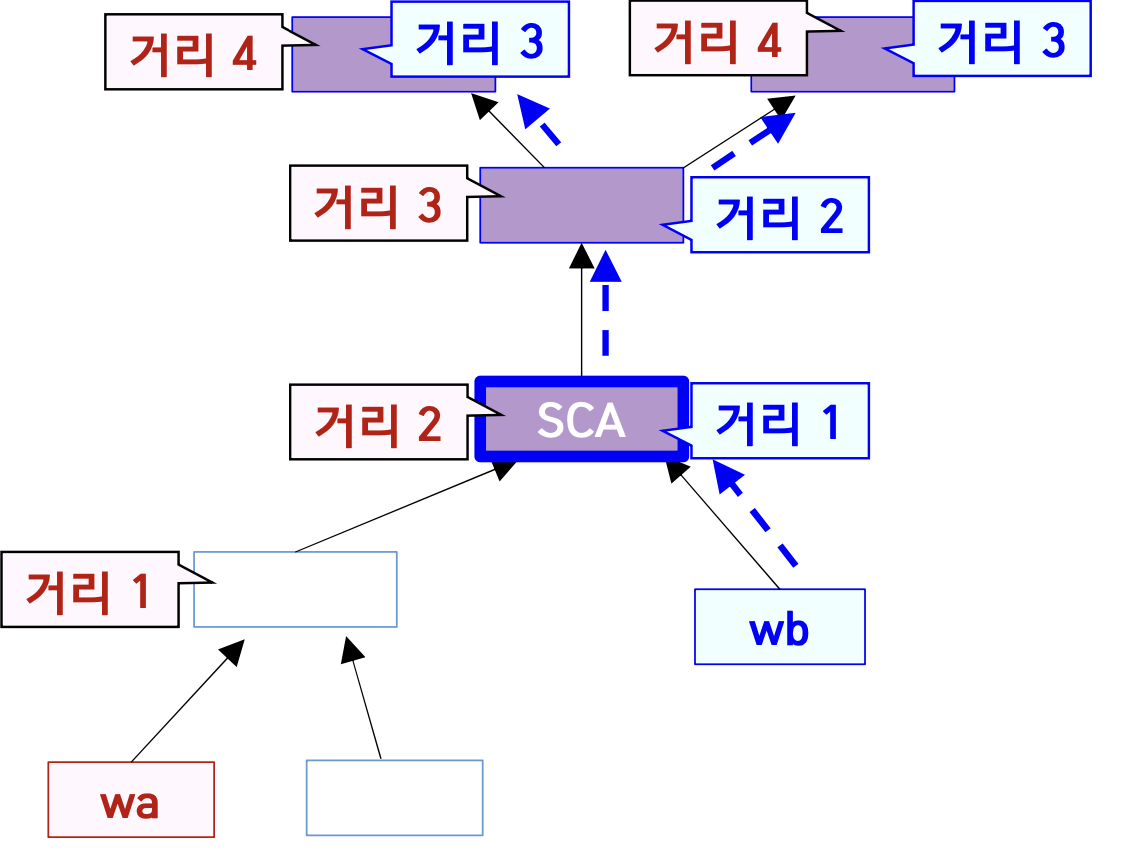
2개의 BFS를 독립적으로 동시에 진행하면 더 작은 영역을 탐색하고도 SCA를 찾을 수 있다.
탐색 중 각 정점에 대한 방문 여부, 지나온 경로, 거리 등을 저장할 때는 출발지가 wa인 경우와 출발지가 wb인 경우로 나누어 별도의 공간에 저장해야 함.
이때, wa와 wb에 해당하는 정점은 각각 둘 이상일 수 있다. (같은 단어의 정점이 둘 이상일 수 있다)
하지만, 서로 다른 단어에서 온 경로끼리 만남만 고려하고, 같은 단어의 서로 다른 정점에서 온 경로끼리 만남은 고려할 필요 없다.
# 수도코드 for sap
sap(graph, aList, bList) :
graph를 탐색해 aList 속한 정점과 bList 속한 정점 간 SCA 하나와 SCA까지 거리 반환
sapLength = math.inf
aList, bList 원소 모두 Queue에 추가
while Queue is not empty :
v = Queue.get()
v 까지 거쳐온 거리 + 1 >= sapLength : break
for w in graph.adj[v] :
if v from aList :
if not visit[w] :
visit[w] = true
Queue.put(w)
if w is in bList :
sapLength = math.min(bLength + curLength, sapLength)
if v from bList :
if not visit[w] :
visit[w] = true
Queue.put(w)
if w is in aList :
sapLength = math.min(aLength + curLength, sapLength) 수행시간 : BFS를 독립적으로 시행하기 때문에 ~O(V+E)에 비례한 시간이 걸린다.
실제 구현
- SAP 구현
def sap(g, aList, bList):
sapLength = (None, math.inf)
fromA, fromB = True, False
aVisit = {}
bVisit = {}
queue = Queue()
for e in aList:
queue.put((e, fromA, 0))
aVisit[e] = 0
for e in bList:
queue.put((e, fromB, 0))
bVisit[e] = 0
if e in aVisit:
sapLength = (e, 0)
while not queue.empty():
v = queue.get()
curVertex = v[0]
curFrom = v[1]
curLength = v[2]
if curLength + 1 >= sapLength[1]: break
for w in g.adj[curVertex]:
if curFrom is fromA:
if w not in aVisit:
aVisit[w] = curLength + 1
queue.put((w, fromA, aVisit[w]))
if w in bVisit:
bLength = bVisit.get(w)
if curLength + bLength + 1 < sapLength[1]:
sapLength = (w, curLength + bLength + 1)
else:
if w not in bVisit:
bVisit[w] = curLength + 1
queue.put((w, fromB, bVisit[w]))
if w in aVisit:
aLength = aVisit.get(w)
if curLength + aLength + 1 < sapLength[1]:
sapLength = (w, curLength + aLength + 1)
return sapLength- Outcast 구현
def outcast(wordNet, wordFileName):
words = set()
filePath = Path(__file__).with_name(wordFileName) # Use the location of the current .py file
with filePath.open('r') as f:
line = f.readline().strip() # Read a line, while removing preceding and trailing whitespaces
while line:
if len(line) > 0:
words.update(line.split())
line = f.readline().strip()
maxDistance = -1
maxDistanceWord = None
for nounA in words:
distanceSum = 0
for nounB in words:
if nounA != nounB:
_, distance = wordNet.sap(nounA, nounB)
distanceSum += distance
if distanceSum > maxDistance:
maxDistance = distanceSum
maxDistanceWord = nounA
return maxDistanceWord, maxDistance, wordsSummary
핵심 1.
Symbol Table에서 value는 제거하고 key만 저장하는 구조를 Set이라고 한다.
Set의 원소는 순서를 가지지 않고 임의의 순서로 재배치 될 수 있다.
핵심 2.
WordNet은 단어 간 의미 관계를 나타내는 그래프이다.
특징
[Entity라는 단어의 Root 하나를 가진다.]
[Cycle이 존재하지 않는다.]
[정점은 유사어 집합, 간선은 의미상 포함관계를 나타내는 그래프이다.]
[같은 단어가 여러 정점에 포함될 수 있다.]
[부모나 자식이 둘 이상일 수 있다.]
핵심 3.
OutCast란 단어의 집합이 주어졌을 때, 가장 의미가 먼 단어를 의미한다.
이를 찾아내기 위해 두 단어 사이의 distance를 측정한다.
이때, distance는 두 단어의 공통조상까지의 최소거리(간선 수의 합)를 의미한다.
핵심 4.
두 정점 사이의 공통조상까지의 거리인 SAP를 찾기 위해 BFS를 병렬로 실행한다.
이때, 각 정점의 경로를 각각 다른 공간에 저장해야한다.
두 정점을 시작점으로 BFS를 수행하기 때문에 수행시간은 O(V+E)에 비례한 시간이 걸린다.
