크루스칼 알고리즘 JS 구현

크루스칼(Kruskal) 알고리즘

크루스칼 알고리즘은 가장 적은 비용(거리)으로 모든 노드를 연결하기 위해 사용하는 알고리즘이며 최소 신장 트리(MST, Minimum Spanning Tree)를 만들기 위한 대표적인 알고리즘이다.

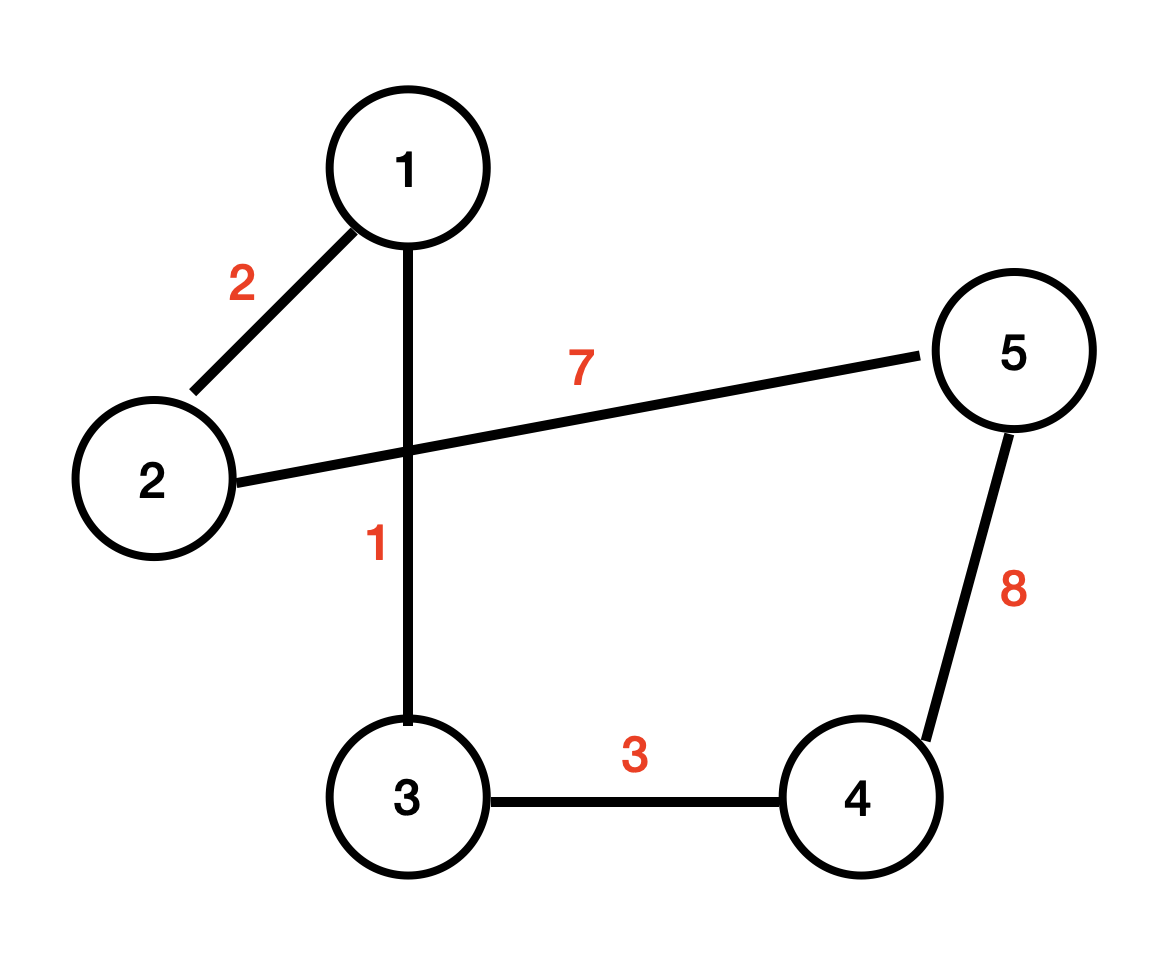
위 그래프가 있다고 가정할 때 노드의 개수는 5개고 간선의 개수는 6개다. 크루스칼 알고리즘의 핵심은 거리가 짧은 순서대로 그래프에 포함시키는 것이다.

간선 정보(비용)를 정리하면 아래와 같다.

• 1번 노드
  1과 2 연결, 비용: 2
  1과 3 연결, 비용: 1
  1과 5 연결, 비용: 2

• 2번 노드
  2과 5 연결, 비용: 7

• 3번 노드
  3과 4 연결, 비용: 3

• 4번 노드
  4과 5 연결, 비용: 8

5번 노드의 간선 정보가 없는 이유는 이미 다른 노드에서 간선 정보를 포함했기 때문이다. 모든 노드를 최소 비용으로 연결시키면 되기 때문에 간선 정보 기준으로 오름차순으로 먼저 정렬한다. 정렬하면 아래와 같다.

/*
edges[i][0], edges[i][1] = 연결된 노드
edges[i][2] = 비용
*/ 

// 정렬 전
edges = [[1, 2, 2], [1, 3, 1], [1, 5, 2], [2, 5, 7], [3, 4, 3], [4, 5, 8]];


// 정렬 후
edges = [[1, 3, 1], [1, 2, 2], [1, 5, 2], [3, 4, 3], [2, 5, 7], [4, 5, 8]];

정렬 후 다음 알고리즘에 맞게 그래프를 연결하면 된다.

1. 정렬된 순서에 맞게 그래프 포함
2. 포함시키기 전 사이클 테이블 확인
3. 사이클을 형성할 경우 패스

사이클이란 그래프가 서로 연결되어 말 그대로 사이클을 형성하는 경우를 뜻한다. 사이클 발생 여부는 Union-Find 알고리즘을 그대로 적용하면 된다.

---

구현

function kruskal(n, arr) {
  // 부모 노드 찾기
  function getParent(set, x) {
    if (set[x] === x) return x;
    return (set[x] = getParent(set, set[x]));
  }

  // 두 개의 노드를 같은 부모 노드로 병합
  function unionParent(set, a, b) {
    a = getParent(set, a);
    b = getParent(set, b);

    // 더 작은 값으로 부모 노드 할당
    if (a < b) set[b] = a;
    else set[a] = b;
  }

  // 같은 부모 노드를 갖는지 확인
  function findParent(set, a, b) {
    a = getParent(set, a);
    b = getParent(set, b);

    if (a === b) return true;
    else return false;
  }

  // 간선의 비용으로 오름차순 정렬
  arr.sort((a, b) => a[2] - b[2]);

  // 사이클 확인을 위한 배열 생성
  // 각 노드가 어느 그래프에 포함되어 있는지 확인하기 위해
  const set = new Array(n);
  for (let i = 1; i <= n; i++) {
    set[i] = i;
  }

  let coast = 0;
  for (let i = 0; i < arr.length; i++) {
    // 동일한 부모를 가르키지 않는 경우에만 선택 -> 사이클이 발생하지 않는 경우
    if (!findParent(set, arr[i][0], arr[i][1])) {
      coast += arr[i][2]; // 비용 추가
      unionParent(set, arr[i][0], arr[i][1]); // 노드 연결
    }
  }

  return coast;
}

const n = 5;
const arr = [
  [1, 2, 2],
  [1, 3, 1],
  [1, 5, 2],
  [2, 5, 7],
  [3, 4, 3],
  [4, 5, 8],
];
console.log(kruskal(n, arr));

---

참고
18. 크루스칼 알고리즘(Kruskal Algorithm)_안경잡이개발자님 블로그