들어가기에 앞서...
이 포스트는 2학년때 수강한 자료구조 수업의 자료와 각종 스터디 블로그를 참고하여 작성되었다.

---

1. 그래프

vertex(정점)와 edge(간선)로 구성된 자료구조.

1.1 그래프의 종류

• 무방향 그래프(undirected graph) : 간선을 나타내는 정점의 쌍에 순서가 없다.
• 방향 그래프(directed graph) : 방향을 가지는 정점의 쌍 <u, v>로 표시
  • u는 꼬리(tail), v는 머리(head)
  • <v, u>와 <u, v>는 서로 다른 간선이다.
• 완전 그래프(complete graph): n개의 정점과 n(n-1)/2개의 간선을 가진 그래프. 즉, 모든 노드가 서로 연결되어있음

1.2 정의

• 그래프의 제한사항
  자기 간선(self edge)또는 자기 루프(self loop) 없음

  자기루프(self-loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다고 한다. 다른 정점을 거치지 않는다.

  동일 간선의 중복 없음

• 경로의 길이(length)
  경로상에 있는 간선의 수

• 단순 경로(simple path)
  처음과 마지막 정점만 같고 나머지는 모두 다름

• 단순 방향 경로(siple directed path)
  

• 사이클(cycle)
  처음과 마지막 정점이 같은 단순 경로
  

• Acyclic (no cycle) graph = Tree
  그래프 관점에서 볼 때, 트리는 사이클이 없는 연결 그래프라 볼 수 있다.

• 차수(degree)
  정점에 부속한 간선들의 수
  

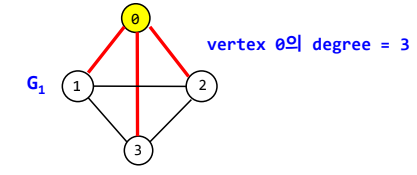
  • 진입차수(in-degree)와 진출차수(out-degree)
    진입차수(in-degree) : 임의의 정점 v가 머리(head)가 되는 간선들의 수
    진출차수(out-degree) : v가 꼬리(tail)가 되는 간선들의 수
    • vertex 1의 degree : 3 (0, 1, 2)
    • vertex 1의 in-degree : 1 (0이 진입)
    • vertex 1의 out-degree : 2 (2, 3으로 진출)

❗ 1.3 그래프 표현법(Graph Representation)

1.3.1 인접 행렬(Adjacency Matrix)

nxn의 2차원 배열

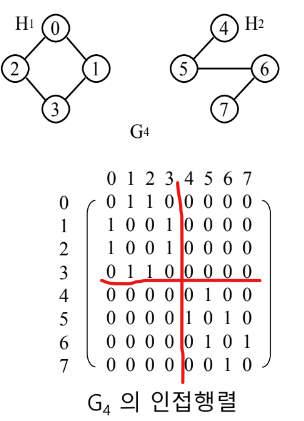
연결되어있으면 1, 연결되어있지 않으면 0
필요 공간 : n^2 비트

장점 : 직관적, 쉬운 구현
단점 : 불필요한 정보 저장, 그래프의 크기가 커지면 메모리 초과 발생 가능

• 무방향 그래프(undirected graph) :
  어떤 정점의 차수는 그 행의 합
• 방향 그래프(directed graph) :
  행의 합은 진출차수
  열의 합은 진입차수
  

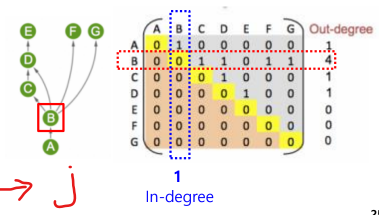
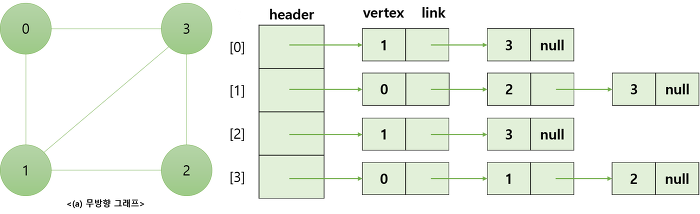
1.3.2 인접 리스트(Adjacency List)

리스트의 노드 구조를 정점필드와 주소(link)필드로 구성하여 정점 i에 대한 인접리스트에 정점 i와 인접한 다른 정점들을 나타내는 노드들을 포함시킨다.

각 정점의 리스트는 헤더 노드를 가지며 리스트 헤더들은 노드 번호의 오름차순으로 정렬되어 있다. => 빠른 접근 가능
❗ (그러나 리스트 내의 노드 순서에는 특별한 의미가 없다.)

장점 : 필요한 정보만 저장하여 메모리 절약
단점 : 인접행렬에 비해 다소 어려움

• 무방향 그래프(undirected graph) :
  n개의 헤드노드, 2e(edge)개의 리스트 노드가 필요
  
• 방향 그래프(directed graph) :
  n개의 헤드노드, e개의 리스트 노드 필요
  

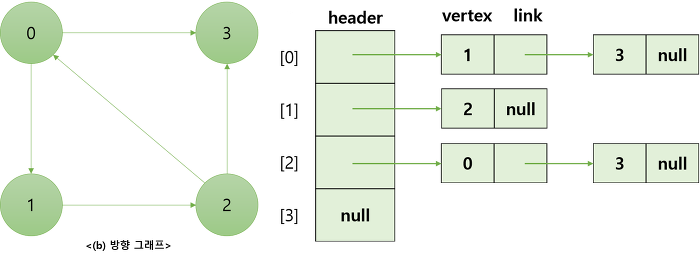
1.3.3 인접 다중 리스트(Adjacency Multilists)

인접리스트(adjacency list)의 문제점을 해소( (0,1)과 (1,0)이 중복되는 문제 )
=> vertex 중심의 인접리스트를 edge중심의 리스트로 변경한다.

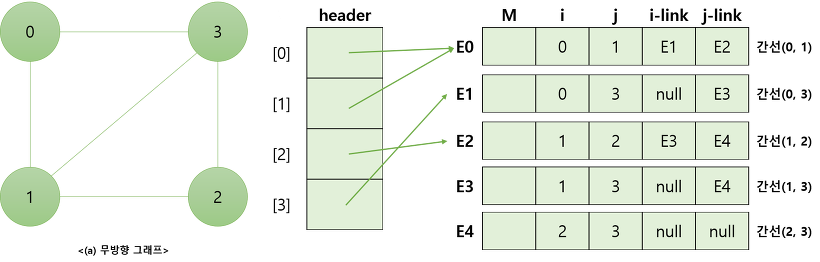
• M : 마크 비트. 이 간선이 이미 검사되었는지 확인
• i, j : 간선에 부속된 정점.
• i-link, j-link : 각 정점의 인접 리스트의 링크

위 그래프에서 vertex 0은 E0으로 이동 후 i-link에 따라 E1으로 이동한다. 그 다음 E1에서 i-link 에 따라 리스트가 끝난다(null을 만남).
같은 원리로 vertex 1의 리스트는 E0 -> E2 -> E3가 된다.

1.4 가중치 간선(Weighted Edges)

그래프 간선에 가중치를 부여한다.

• 인접행렬 : 행렬에 a[i][j]의 가중치 정보를 저장한다.
  
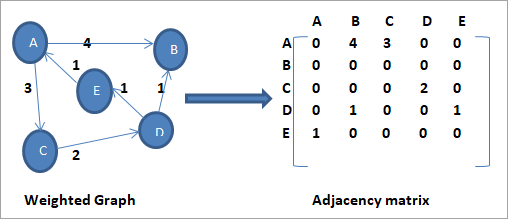
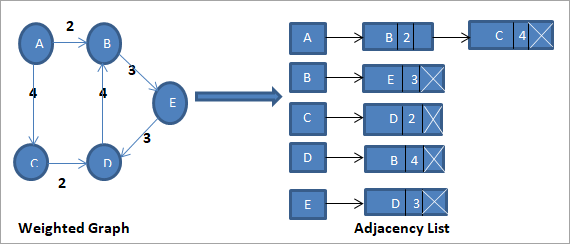
• 인접리스트 : 노드 구조에 weight 필드를 추가한다.
  

참고

그래프 - https://m.blog.naver.com/occidere/220923695595
자기 루프 정의 - https://velog.io/@kaitlin_k/graph
인접리스트, 다중 인접리스트 - https://kingpodo.tistory.com/46
가중치 간선 그림 - https://www.softwaretestinghelp.com/graph-implementation-cpp/