[백준] 11057 오르막 수

iamjinseo·2022년 7월 7일

다이나믹 프로그래밍 백준

문제풀이-Python

목록 보기

16/134

문제

오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.

예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.

수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.

입출력

입력

첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.

출력

첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.

입출력 예시

해설

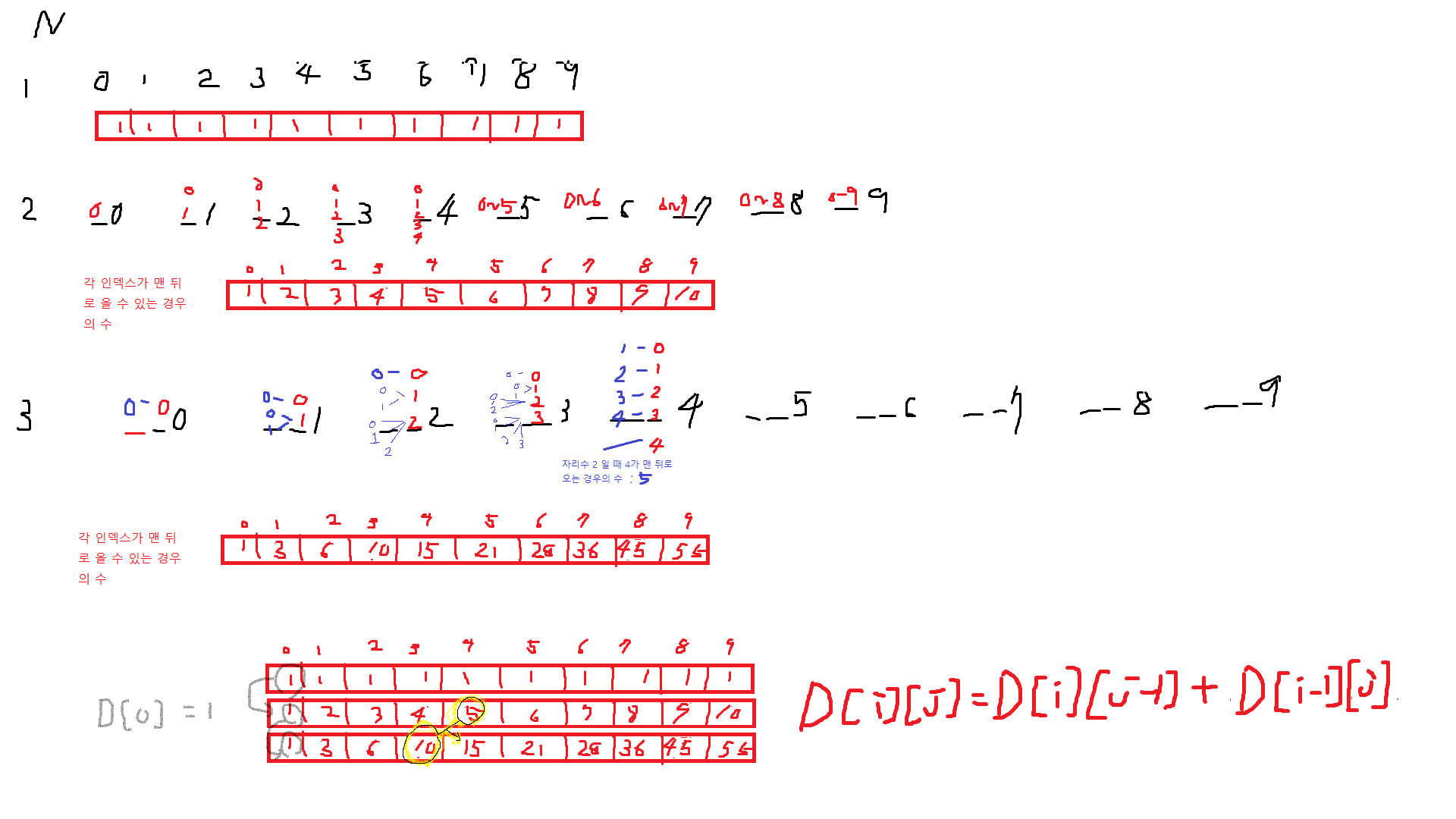
계단수랑 비슷하다.

예시 - 자리수 3일 때(N이 3일 때)

1) N이 1일 때 0~9의 수가 맨 뒤로 올 경우는 전부 1이다.

1 1 1 1 1 1 1 1 1

2) N이 2일 때 0~9의 수가 맨 뒤로 올 경우는 다음과 같다.

1 2 3 4 5 6 7 8 9

0앞에는 0만 오고, 1 앞에는 0과 1이 오고, 2 앞에는 0, 1, 그리고 2가 올 수 있으므로 개수가 하나씩 늘어감

3) N이 3일 때 0~9의 수가 맨 뒤로 올 경우는 다음과 같다.

1 3 6 10 15 21 25 36 45 56
1. 0 앞에는 0만 올 수 있으므로 경우의 수 1
2. 1 앞에는 0과 1이 올 수 있다.
  2-1. 0앞에는 0만 올 수 있으므로 경우의 수 1
  2-2. 두 자리 수 였을 때 1이 뒤에 있고 앞에 오는 수는 0과 1이었으므로 경우의 수 2
  2-3. 따라서 총 경우의 수는 3
3. 2~9의 수가 맨 뒤로 나올 때의 경우의 수를 위와 같은 방식으로 계산해본다.

어랏 보다보니 점화식이 생각나려 한다...
그림의 배열에서 보면 한 칸의 경우의 수는 왼쪽 값이랑 위에 값을 더한 것이다..!

D[0]=1,
D[i][j]=D[i][j-1]+D[i-1][j] (j가 1이상 9이하)

코드

# 백준 11057 오르막 수 / 실버1
# dp

# 첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다. (자리수)
N = int(input())

# 이중 리스트 만들기
dp = [[0]*10 for _ in range(N+1)]

# 첫째 줄(자리수 하나)는 모두 1로 넣기
for i in range(10):
    dp[1][i] = 1

# dp계산 (두 자리 수부터)
for i in range (2, N+1):
    dp[i][0]=1 #맨 뒷자리 수가 0인 경우의 수는 무조건 하나
    for j in range(1, 10):
        dp[i][j]=dp[i][j-1]+dp[i-1][j]

# 첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.
print(sum(dp[N])%10007)