[백준] 2193 이친수

iamjinseo·2022년 7월 7일

문제풀이-Python

목록 보기

17/134

문제

0과 1로만 이루어진 수를 이진수라 한다. 이러한 이진수 중 특별한 성질을 갖는 것들이 있는데, 이들을 이친수(pinary number)라 한다. 이친수는 다음의 성질을 만족한다.

이친수는 0으로 시작하지 않는다.
이친수에서는 1이 두 번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다.
예를 들면 1, 10, 100, 101, 1000, 1001 등이 이친수가 된다. 하지만 0010101이나 101101은 각각 1, 2번 규칙에 위배되므로 이친수가 아니다.

N(1 ≤ N ≤ 90)이 주어졌을 때, N자리 이친수의 개수를 구하는 프로그램을 작성하시오.

입출력

입력

입력
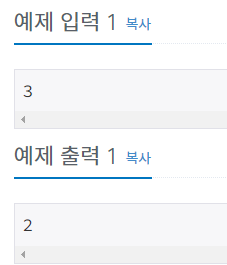
첫째 줄에 N이 주어진다.

출력

출력
첫째 줄에 N자리 이친수의 개수를 출력한다.

입출력 예시

해설

2차원 리스트로 해결

자리수에 따라서, 0과 1이 맨 뒷자리로 올 수 있는 경우의 수를 1차원 배열에 넣고,
자리수마다 나온 배열들을 합쳐 2차원 리스트로 만들고 그 리스트 안에서 규칙을 찾아 점화식을 세우는 방법

점화식 세우기는 아래 해설 그림 참고

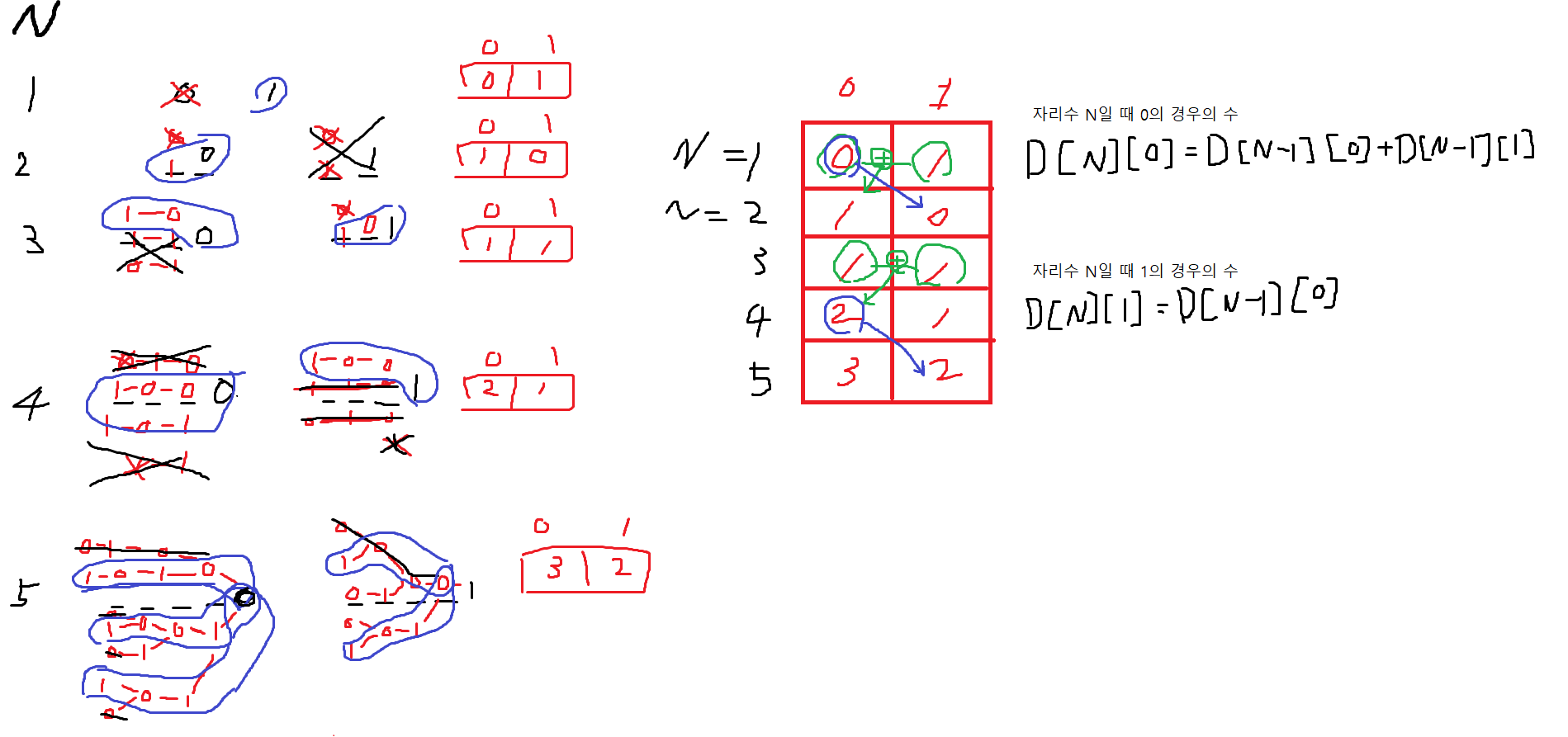
dp[N][0] = dp[N-1][0]+dp[N-1][1]
dp[N][1] = dp[N-1][0]

dp[N] = dp[N][0]+dp[N][1]

1차원 리스트로 해결

자리수에 따라 나올 수 있는 경우의 수를 구해본 다음 수에서 규칙을 찾아 점화식을 세우는 방법

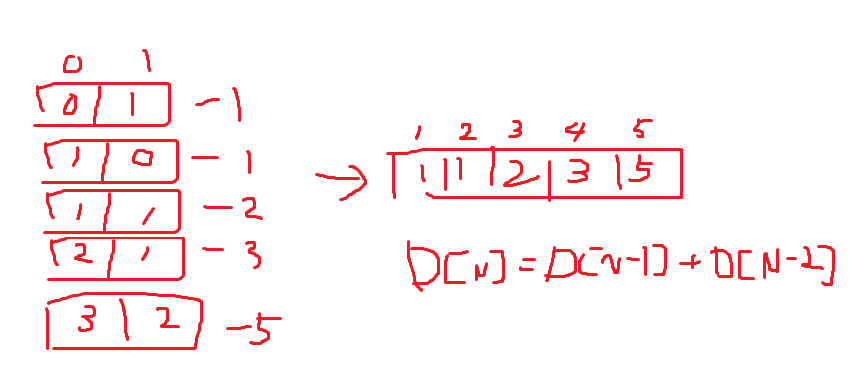
dp[N][0] = dp[N][0]+dp[N][1]

코드

첫 번째 방법

# 첫째 줄에 N이 주어진다. N은 0이상 90이하
N = int(input())

# dp 만들기
# 이중 리스트로
dp = [[0]*2 for _ in range(N+1)]

# dp 값 넣어보기
# 해설은 그림 참고
dp[1][0]=0
dp[1][1]=1

for i in range(2, N+1):
    for j in range(2):
        dp[i][0] = dp[i-1][0]+dp[i-1][1]
        dp[i][1] = dp[i-1][0]

# 첫째 줄에 N자리 이친수의 개수를 출력한다.
print(sum(dp[N]))

두 번째 방법

#이중리스트 없이 1차원으로도 가능
# 첫째 줄에 N이 주어진다. N은 0이상 90이하
N = int(input())

dp = [0]*91
dp[1]=1
dp[2]=1

for i in range(3, 91):
    dp[i]=dp[i-1]+dp[i-2]

print(dp[N])