문제

2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×17 직사각형을 채운 한가지 예이다.

입출력

입력

첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)

출력

첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.

예시

---

해설

다이나믹 프로그래밍

2×n 타일링 풀이법처럼 다이나믹프로그래밍의 Bottom-up방식으로 해결한다.

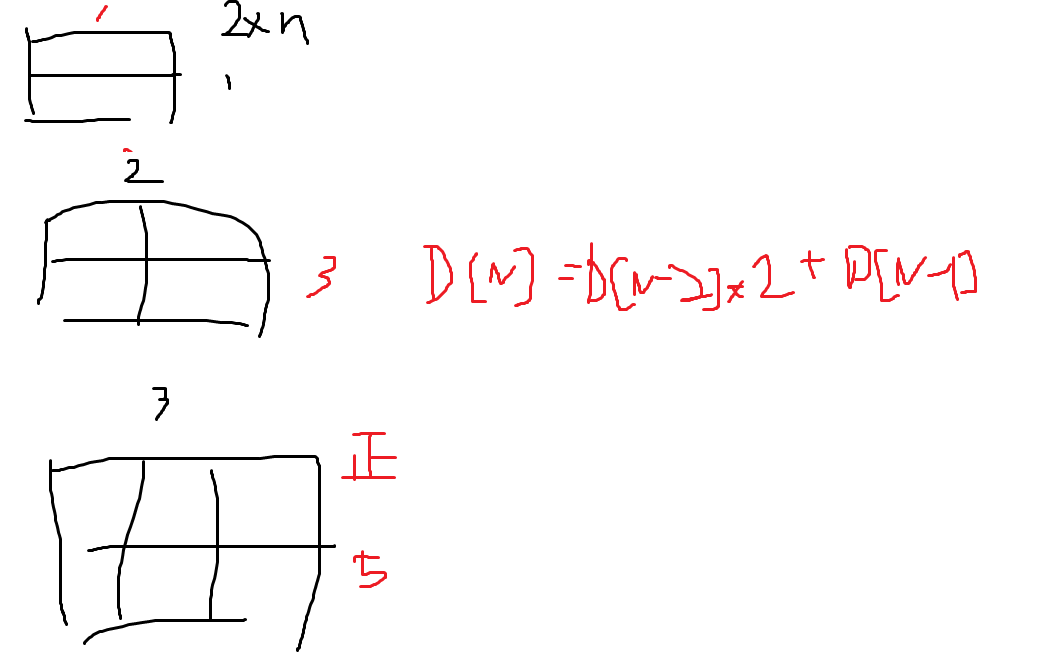
위에서부터 2x1, 2x2, 2x3 직사각형이고 각 직사각형에 대한 경우의 수는 1 3 5이다.

D[N] = D[N-1] + 2*D[N-2]

물론 n이 4일 때의 경우의 수, 5일 때의 경우의 수를 고려하여 점화식을 추려내야 하지만 해설이 길어짐을 우려하여 간단하게 표현함.
** 3 - 다이나믹 프로그래밍 해설 참고

코드

# 2×n 타일링 2
#입력 : 첫째 줄에 n이 주어진다. n은 1 이상 1000이하

# 점화식 D[n]=D[n-1]+2*D[n-2]

# 입력
n = int(input())

# 2xn 직사각형을  1×2, 2×1과 2×2 타일로 채우는 방법의 수를 넣는 배열
dp = [0]*1001

# 2x1 직사각형의 경우의 수는 1
dp[1] = 1

# 2x2 직사각형 경우의 수는 3
dp[2] = 3

# 2x1000까지 경우의 수 계산
for i in range(3, n+1):
    # 점화식
    dp[i]=dp[i-1]+(2*dp[i-2])

# 출력 : 첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
print(dp[n]%10007)

#다이나믹프로그래밍