문제

정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.

• 1+1+1+1
• 1+1+2
• 1+2+1
• 2+1+1
• 2+2
• 1+3
• 3+1

정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.

입출력

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.

출력

각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.

입출력 예시

<입력>
3
4
7
10
<출력>
7
44
274

---

해설

1을 더할 때는 1만 필요하므로 경우의 수는 1
2를 더할 때는 1+1과 2가 필요하므로 경우의 수는 2
3을 더할 때는 1+1+1과 1+2, 2+1, 3이 필요하므로 경우의 수는 3


4를 더할 때는 문제에 나온 예시와 같이 7가지의 경우의 수가 존재하지만 저렇게 일일이 더할 필요 없다.

4는 3+1과 2+2, 1+3으로 표현할 수 있다.

그렇다고 해서 경우의 수가 3인 건 아니다.

• 3+1 으로 표현할 때
  3를 더하는 모든 경우에 1만 더하면 4가 된다.
  3을 더하는 경우의 수는 3이다.
  => 3+1 으로 표현할 때의 경우의 수는 3이다.
• 2+2 로 표현할 때
  2를 더하는 모든 경우에 2만 더하면 4가 된다.
  2를 더하는 경우의 수는 2이다.
  => 2+2 으로 표현할 때의 경우의 수는 2이다.
• 1+3 으로 표현할 때
  1을 더하는 모든 경우에 3만 더하면 4가 된다.
  1을 더하는 경우의 수는 1이다.
  => 1+3 으로 표현할 때의 경우의 수는 1이다.

4를 1,2,3의 합으로 나타내는 경우의 수는 3+2+1 = 7이다.

앞으로 나오는 11까지의 모든 수 또한 위와 같은 방법으로 구할 수 있다.

해설 그림

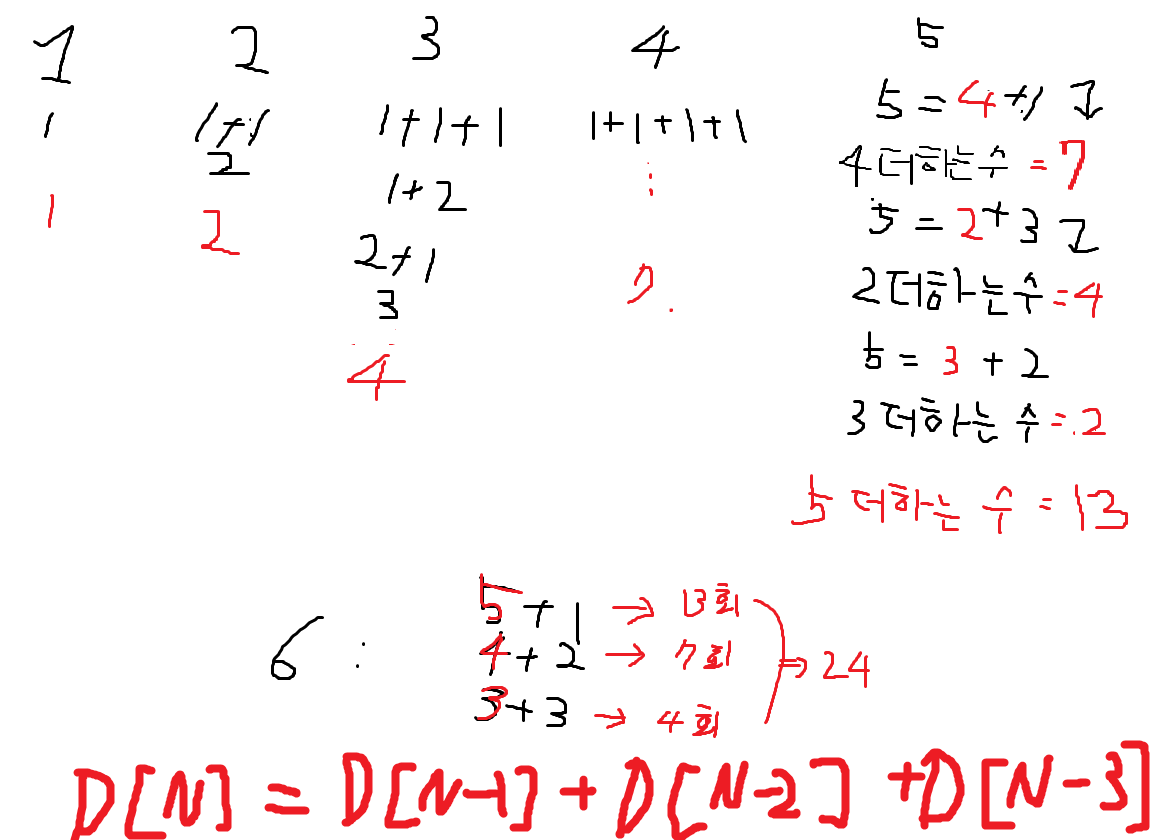
코드

# 1,2,3 더하기
# 다이나믹 프로그래밍
# 정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
# 1+1+1+1
# 1+1+2
# 1+2+1
# 2+1+1
# 2+2
# 1+3
# 3+1

# 입력 : 첫째 줄에 테스트 케이스의 개수 T가 주어진다. 
# 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. 
T = int(input())

# n은 양수이며 11보다 작다.
# Bottom-up으로 모든 경우의 수 구하기
dp = [0]*12
dp[1] = 1
dp[2]=2
dp[3] = 4
dp[4] = 7

#점화식은 D[N] = D[N-1]+D[N-2]+D[N-3]
for i in range(5, 12):
    dp[i] = dp[i-1]+dp[i-2]+dp[i-3]

#모든 경우의 수를 다 구했으므로 T번동안 원하는 숫자를 입력받아서
# 2xn의 경우의 수(dp[n])를 출력하자.
answer="" #정답 출력용 문자열. 자바의 StringBuilder같은 역할
for i in range(0, T):
    n = int(input())
    answer += str(dp[n])+"\n"

print(answer)

#다이나믹프로그래밍

---

고난

• 1, 2, 3 만 더해야 한다는 걸 모르고 5를 구할 때 1+4로 처리해 버렸다.
  그러면 경우의 수가 하나 더 나옴...
• 2의 경우의 수가 2(1+1, 2)인데 자기 자신도 포함하는지 모르고 1+1만 있는 줄 알아서 경우의 수를 1로 처리해버림...
  그래서 1의 경우의 수 1(1),
  2의 경우의 수 1(1+1),
  3의 경우의 수 3(1+1+1, 1+2, 2+1)이라 생각했고
  4의 경우의 수는 7이므로 점화식이 D[N]=2*D[N-1]+D[N-2] 인줄 알았다..