
https://www.acmicpc.net/problem/2458
문제 설명
1번부터 N번까지 번호가 붙여져 있는 학생들에 대하여 두 학생끼리 키를 비교한 결과의 일부가 주어져 있다. 단, N명의 학생들의 키는 모두 다르다고 가정한다. 예를 들어, 6명의 학생들에 대하여 6번만 키를 비교하였고, 그 결과가 다음과 같다고 하자.
1번 학생의 키 < 5번 학생의 키
3번 학생의 키 < 4번 학생의 키
5번 학생의 키 < 4번 학생의 키
4번 학생의 키 < 2번 학생의 키
4번 학생의 키 < 6번 학생의 키
5번 학생의 키 < 2번 학생의 키이 비교 결과로부터 모든 학생 중에서 키가 가장 작은 학생부터 자신이 몇 번째인지 알 수 있는 학생들도 있고 그렇지 못한 학생들도 있다는 사실을 아래처럼 그림을 그려 쉽게 확인할 수 있다. a번 학생의 키가 b번 학생의 키보다 작다면, a에서 b로 화살표를 그려서 표현하였다.
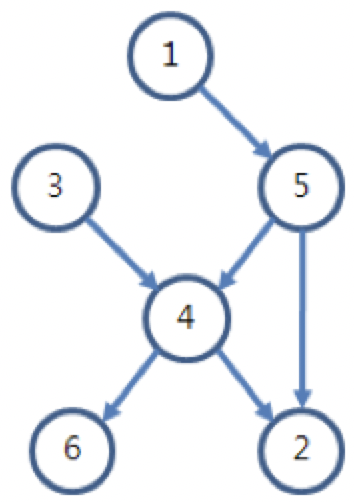
1번은 5번보다 키가 작고, 5번은 4번보다 작기 때문에, 1번은 4번보다 작게 된다. 그러면 1번, 3번, 5번은 모두 4번보다 작게 된다. 또한 4번은 2번과 6번보다 작기 때문에, 4번 학생은 자기보다 작은 학생이 3명이 있고, 자기보다 큰 학생이 2명이 있게 되어 자신의 키가 몇 번째인지 정확히 알 수 있다. 그러나 4번을 제외한 학생들은 자신의 키가 몇 번째인지 알 수 없다.
학생들의 키를 비교한 결과가 주어질 때, 자신의 키가 몇 번째인지 알 수 있는 학생들이 모두 몇 명인지 계산하여 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 학생들의 수 N (2 ≤ N ≤ 500)과 두 학생 키를 비교한 횟수 M (0 ≤ M ≤ N(N-1)/2)이 주어진다. 다음 M개의 각 줄에는 두 학생의 키를 비교한 결과를 나타내는 두 양의 정수 a와 b가 주어진다. 이는 번호가 a인 학생이 번호가 b인 학생보다 키가 작은 것을 의미한다.
출력
자신이 키가 몇 번째인지 알 수 있는 학생이 모두 몇 명인지를 출력한다.
풀이
문제 속에 답이 있습니다
나보다 위에있는 노드 + 아래에 있는 노드가 N-1이면 등수 알 수 있음
n 뒤에 몇명 + n 앞에 몇명 = N-나이면나는 그 중간에 껴있다는 것이다.
- 다른 노드를 경유해서라도 어떤 노드로 갈 수 있는지 검사 -> 플로이드 워셜
- 인접행렬에서 N이 행일 때 true개수 + N이 열일 때 true개수가 N-1이면 res+1
import java.io.*;
import java.util.*;
public class B2458_키순서 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int res = 0;
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
// 인접행렬 기본적으로 false으로 초기화 => 만날 수 없다는 뜻
boolean[][] adjMatrix = new boolean[N + 1][N + 1];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adjMatrix[from][to] = true;
} // end input. end create adjacent matrix
// Floyd-Warshall: i노드에서 다른 노드를 경유해서라도 j로 갈 수 있는지 검사
for (int k = 1; k <= N; k++) { // 경유 노드
for (int i = 1; i <= N; i++) { // 출발 노드
if (i == k) continue;
for (int j = 1; j <= N; j++) { // 도착 노드
if (i == j || j == k) continue;
// i 에서 j로 갈 수 있음
if(adjMatrix[i][k] && adjMatrix[k][j]) {
adjMatrix[i][j] = true;
}
}
}
} // end Floyd
// 인접행렬에서, 어떤 수 n이 행일 때 true인 수 + 어떤 수 n이 열일 때 true인 수 = N-1이면 가능
// n 뒤에 몇명 + n 앞에 몇명 = N-나 이면 나는 그 중간에 껴있다는 것이다.
for (int i = 1; i <= N; i++) {
int cnt = 0;
// i가 행일 때
for (int j = 1; j <= N; j++) {
if(i==j) continue;
if(adjMatrix[i][j]) cnt++;
}
for (int j = 1; j <= N; j++) {
if(i==j) continue;
if(adjMatrix[j][i]) cnt++;
}
if(cnt==N-1) res++;
}
System.out.println(res);
}
}어째서 플로이드 워셜인가?
예제 2에서 등수 확인이 가능한 4를 살펴보자.
4는 플로이드 워셜을 통해 6, 2에 도달할 수 있다. 도달할 수 있다는 건 나보다 자식이라는 뜻이고 그것은 곧 "나보다 큰" 학생이라는 걸 알 수 있다.
그리고 인접행렬을 보면 4행에 6, 2열에 true(도달할 수 있다는 뜻)가 새겨질 것이다.
그리고 1, 3, 5가 플로이드 워셜을 통해 4에 도달할 것이다. 그것들이 도달했다는 건 4보다 부모라는 뜻이고 그것은 곧 "나보다 작은"학생이라는 걸 알 수 있다.
그리고 인접행렬을 보면 1, 3, 5행의 4열에 true가 새겨질 것이다.
다른 노드들 또한 플로이드 워셜을 통해 인접행렬에 또다른 노드로의 도달 가능성이 새겨져있을 것이다.
그렇다면 플로이드 워셜 종료 후 어떤 노드 n에 대해 "나보다 작다 또는 크다"의 정보가 true 또는 false로 나타날 것이다.
여기서 n을 행으로 취할 때의 true갯수와 열로 취할 때 true갯수를 더하면 나보다 크고 작은 애들의 합이고, 이들이 N-1개라면 n은 등수를 알 수 있다.
결과

후기
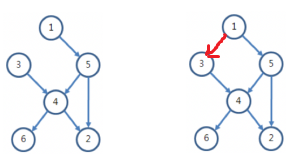
처음에는 부모노드가 없거나, 부모노드의 자식과 관계가 있다면(이동할 수 있다면) 등수를 알 수 있다고 생각했다. (1, 2번 예시를 보고)
그러나 3번 예시를 보고 그것은 완전히 틀렸다는 것을 알 수 있었다.
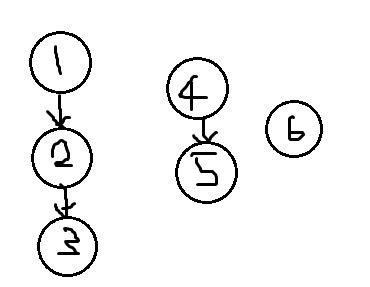
3번 예시를 그려보았다.
내 논리로 따지면 다른 노드 다 된다.
결국 문제를 천천히 읽어보고 문제에 답이 있다는 걸 알았다.
