https://school.programmers.co.kr/learn/courses/30/lessons/12943
1937년 Collatz란 사람에 의해 제기된 이 추측은, 주어진 수가 1이 될 때까지 다음 작업을 반복하면, 모든 수를 1로 만들 수 있다는 추측입니다. 작업은 다음과 같습니다.

1-1. 입력된 수가 짝수라면 2로 나눕니다.
1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다. 
2. 결과로 나온 수에 같은 작업을 1이 될 때까지 반복합니다.

예를 들어, 주어진 수가 6이라면 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1 이 되어 총 8번 만에 1이 됩니다. 위 작업을 몇 번이나 반복해야 하는지 반환하는 함수, solution을 완성해 주세요. 단, 주어진 수가 1인 경우에는 0을, 작업을 500번 반복할 때까지 1이 되지 않는다면 –1을 반환해 주세요.

제한 사항
입력된 수, num은 1 이상 8,000,000 미만인 정수입니다.

입출력 예
n result
6 8
16 4
626331 -1

입출력 예 설명
입출력 예 #1
문제의 설명과 같습니다.

입출력 예 #2
16 → 8 → 4 → 2 → 1 이 되어 총 4번 만에 1이 됩니다.

입출력 예 #3
626331은 500번을 시도해도 1이 되지 못하므로 -1을 리턴해야 합니다.

풀이

def solution(num):
    cnt =0
    while num!=1: #num이 1이될 때까지
        if num%2: # num이 홀수일 때(num이 짝수면 0이 나오고 else로 감)
            num = num*3 + 1
            cnt+=1
        else: #num이 짝수면
            num /=2 
            cnt += 1
    return cnt if cnt<500 else -1

처음에는 dp로 풀려고 했는데, 홀수 수 계산할 때 더 큰 수의 dp가 필요함을 알게돼서 그렇겐 안함.
dp[3]을 구하기 위한 과정=>(dp[3] = dp[10]+1, dp[10]=dp[5]+1, dp[5]=dp[16]+1)

결과

그냥 구현했는데 나쁘지 않음

남의 코드

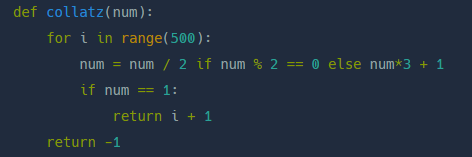
일단 계산 횟수가 500까지여야되는 걸 for로 처리한 게 놀라움!
그리고 내가 쓴 조건문을 줄여놓은 듯 해 간결해 보임

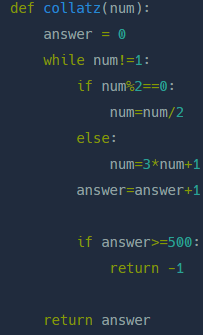
그리고 다른 사람들은 반복문 내에서 cnt가 500이상이 되면 멈추도록 한 반면 나는 계산이 다 끝나고 cnt가 500이 넘으면 -1이 리턴되게 했다. 실행시간 면에서 차이가 많이 날 것 같다.