🎈 깊이 우선 탐색 - DFS (Depth-First Search)
"깊이 우선 탐색(DFS)이란 그래프 탐색 알고리즘 중에서 루트 노드(또는 다른 임의의 노드)에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다. 주로, 모든 노드를 방문하고자 하는 경우에 사용된다."
그래프 탐색이란?
: 하나의 정점에서 시작해서 차례대로 모든 정점에 방문하는 것
대표적인 그래프 탐색 방법으로는 너비 우선 탐색과 깊이 우선 탐색이 존재한다. 그 중 깊이 우선 탐색에 대해서 알아보고자 한다.
💡 DFS 특징
- 자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있다.
- 재귀로 함수를 호출하는 방식으로 동작된다.
- 재귀를 사용하지 않고 스택 자료구조를 이용하는 방법도 존재한다.
- 어떤 노드를 방문했는지 검사한다.
- 이미 방문한 노드를 다시 방문하여 처리하게 되면 무한 루프에 빠질 수 있다. 그렇기 때문에 그래프 탐색에서는 방문한 노드를 처리하는 로직이 필요하다.
- 스택(Stack) 자료구조를 사용한다.
- 후입선출(LIFO) 방식으로 가장 최근에 방문한 노드 먼저 처리한다.
💨 DFS 과정
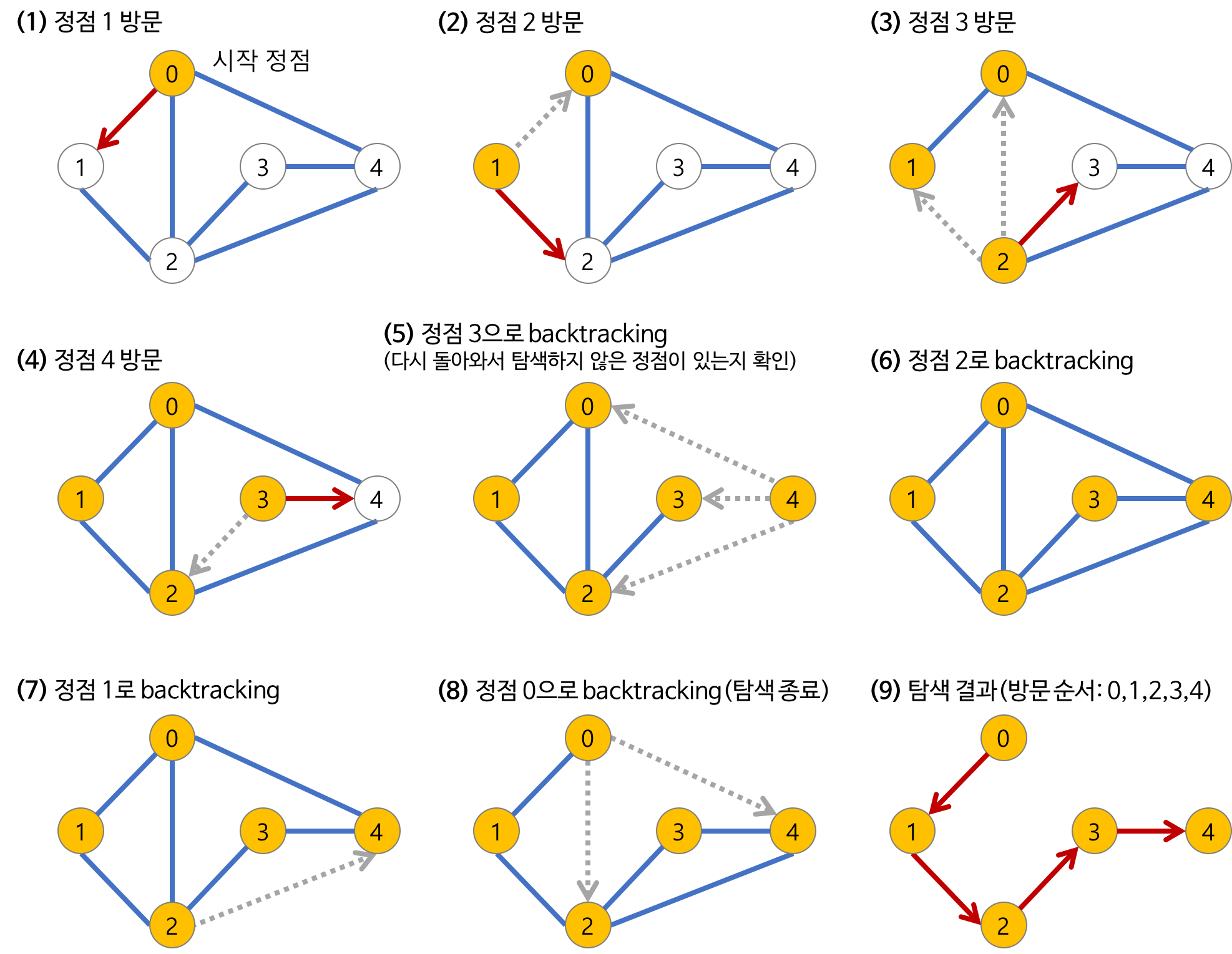
(1)시작 정점과 연결된 노드를 찾아 방문한다.(2) ~ (4)방문한 노드와 연결된 노드를 방문한다.(5)노드 3으로 돌아와서 노드 3과 연결된 노드 중 방문하지 않은 노드가 있는지 확인한다.
- 만약 있으면(2) ~ (4)과정을 반복한다.(6) ~ (9)위 과정을 반복하고 루트 노드로 돌아왔을 때 탐색을 종료한다.
💫 시간 복잡도
위와 같은 그래프를 구현하는 방법으로는 인접행렬과 인접 리스트 방식으로 구현할 수 있다.
인접 행렬: 2차원 배열
인접 리스트: LinkedList, ArrayList ..
인접 행렬 시간복잡도 : O(N^2)
인접 리스트 시간복잡도 : O(N+E)
N: 노드의 수
E: 간선의 수
📌 예제
val graph = mutableListOf<MutableList<String>>()
val result = mutableListOf<String>()
val dx = listOf(-1, 1, 0, 0)
val dy = listOf(0, 0, -1, 1)
fun main() {
repeat(5) {
graph.add(readln().split(" ").toMutableList())
}
for (i in 0 until 5) {
for (j in 0 until 5) {
dfs(i to j, graph[i][j])
}
}
println(result.count())
}
fun dfs(start: Pair<Int, Int>, s: String) {
if (s.length == 6) {
if (s !in result) {
result.add(s)
}
return
}
val x = start.first
val y = start.second
for (i in 0 until 4) {
val a = x + dx[i]
val b = y + dy[i]
if (a in 0 until 5
&& b in 0 until 5) {
dfs(a to b, s + graph[a][b])
}
}
}재귀 호출 방식을 활용하였다.
val graph = mutableListOf<MutableList<String>>()
val result = mutableListOf<String>()
val dx = listOf(-1, 1, 0, 0)
val dy = listOf(0, 0, -1, 1)
fun main() {
repeat(5) {
graph.add(readln().split(" ").toMutableList())
}
for (i in 0 until 5) {
for (j in 0 until 5) {
dfs(i to j, graph[i][j])
}
}
println(result.count())
}
fun dfs(start: Pair<Int, Int>, ss: String) {
val stack = Stack<Triple<Int, Int, String>>()
stack.add(Triple(start.first, start.second, ss))
while (stack.isNotEmpty()) {
val (x, y, s) = stack.pop()
if (s.length == 6) {
if (s !in result) {
result.add(s)
}
continue
}
for (i in 0 until 4) {
val a = x + dx[i]
val b = y + dy[i]
if (a in 0 until 5
&& b in 0 until 5) {
stack.add(Triple(a, b, s + graph[a][b]))
}
}
}
}stack 자료구조를 활용하였다.

