[Algorithm] 너비 우선 탐색 - BFS(Breadth-First Search)

🎈 너비 우선 탐색 - BFS (Breadth-First Search)

"너비 우선 탐색(BFS)이란 그래프 탐색 알고리즘 중에서 인접한 노드를 먼저 탐색하는 방식이다. 주로 두 노드 사이의 최단 경로를 찾을 때 사용된다."

그래프 탐색이란?
: 하나의 정점에서 시작해서 차례대로 모든 정점에 방문하는 것

대표적인 그래프 탐색 방법으로는 너비 우선 탐색과 깊이 우선 탐색이 존재한다. 그 중 너비 우선 탐색에 대해서 알아보고자 한다.

---

💡 BFS 특징

1. 재귀로 호출하지 않는다.
   • 깊이 우선 탐색(DFS)은 재귀로 호출하는 방식이지만 너비 우선 탐색(BFS)은 재귀를 사용하지 않는다.
2. 어떤 노드를 방문했는지 검사한다.
   • 이미 방문한 노드를 다시 방문하여 처리하게 되면 무한 루프에 빠질 수 있다. 그렇기 때문에 그래프 탐색에서는 방문한 노드를 처리하는 로직이 필요하다.
3. 큐(Queue) 자료구조를 사용한다.
   • 선입선출(FIFO) 방식으로 먼저 방문한 노드 순서대로 처리한다.

---

💨 BFS 과정

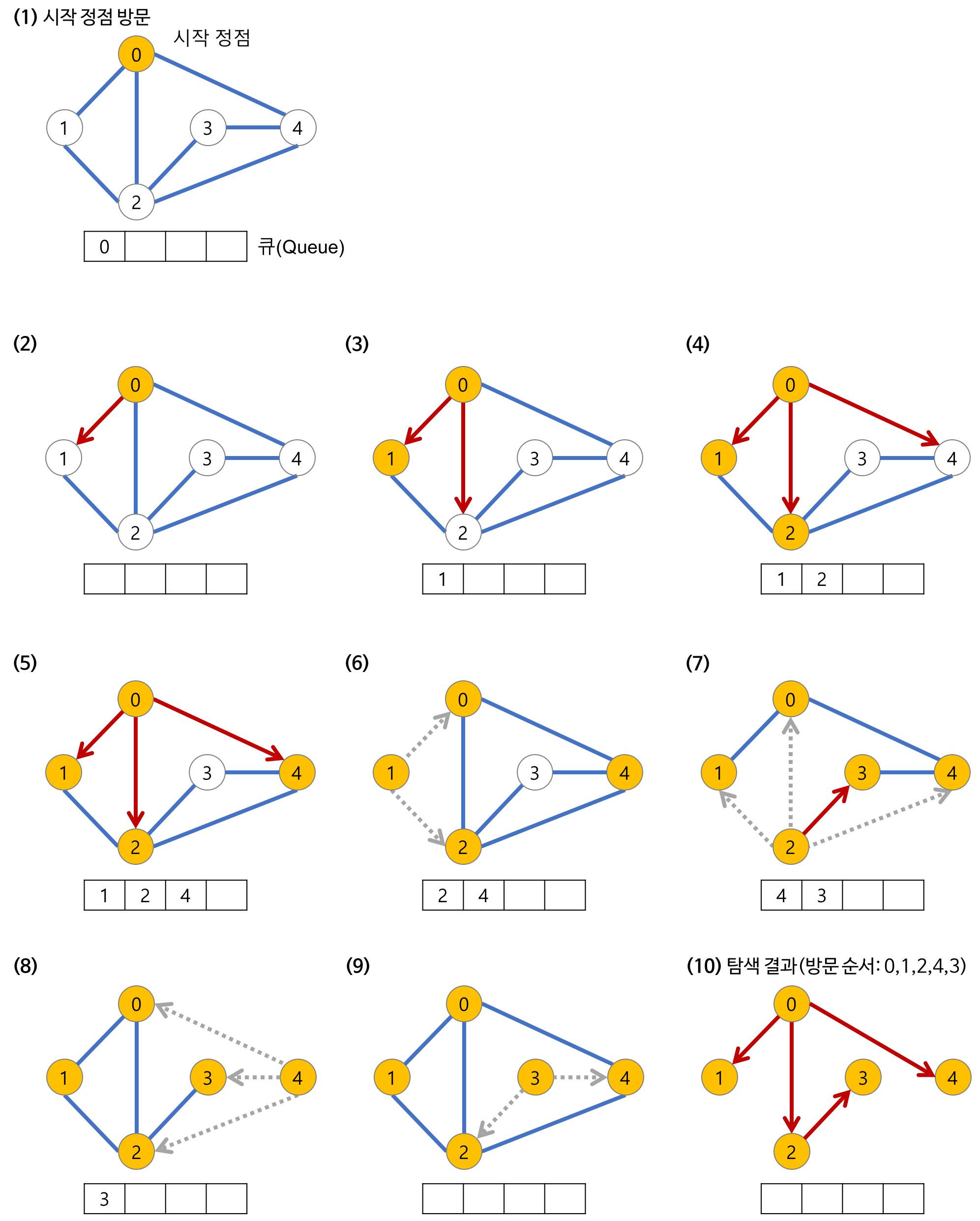
(1). 처음으로 시작 정점에 방문을 하며 큐에 시작 노드를 추가해준다.
(2) ~ (5). 큐에 노드를 빼내고 해당 노드와 연결된 다른 노드들을 찾아 방문한다. 이때 방문을 하면 큐에 노드를 추가해준다. 만약 이미 방문한 노드라면 무시한다.
(6) ~ (10). 과정을 반복하며 큐에 노드가 없을 때 종료된다.

---

💫 시간 복잡도

위와 같은 그래프를 구현하는 방법으로는 인접행렬과 인접 리스트 방식으로 구현할 수 있다.

인접 행렬: 2차원 배열
인접 리스트: LinkedList, ArrayList ..

인접 행렬 시간복잡도 : O(N^2)
인접 리스트 시간복잡도 : O(N+E)
N: 노드의 수
E: 간선의 수

---

📌 예제

1388번: 바닥 장식

var n = 0
var m = 0
val graph = mutableListOf<List<Char>>()
val visited by lazy { Array(n) { Array(m) { 0 } } }
var cnt = 0
fun main() {
    val (_n, _m) = readln().split(' ').map { it.toInt() }
    n = _n
    m = _m
    repeat(n) {
        graph.add(readln().toList())
    }

    for (i in 0 until n) {
        for (j in 0 until m) {
            bfs(i to j)
        }
    }

    println(cnt)
}

fun bfs(start: Pair<Int, Int>) {
    val q: Queue<Pair<Int, Int>> = LinkedList()
    q.add(start)

    if (visited[start.first][start.second] == 0) {
        visited[start.first][start.second] = 1
        cnt += 1
    } else return

    while (q.isNotEmpty()) {
        val (x, y) = q.poll()

        var a = x
        var b = y
        if (graph[x][y] == '-') b += 1 else a += 1

        if (a in 0 until n
            && b in 0 until m
            && visited[a][b] == 0
            && graph[start.first][start.second] == graph[a][b]) {
            visited[a][b] = 1
            q.add(a to b)
        }
    }
}

그래프가 행렬일때는 Queue에 Pair형태로 x, y 좌표가 들어간다.

2644번: 촌수계산

lateinit var graph: Array<MutableList<Int>>
lateinit var visited: Array<Int>
fun main() {
    val n = readln().toInt()
    val (x, y) = readln().split(' ').map { it.toInt() }
    graph = Array(n+1) { mutableListOf() }
    visited = Array(n+1) { 0 }

    val m = readln().toInt()
    repeat(m) {
        val (a, b) = readln().split(' ').map { it.toInt() }
        graph[a].add(b)
        graph[b].add(a)
    }

    println(BFS(x, y))
}

fun BFS(start: Int, end: Int): Int {
    val q: Queue<Pair<Int, Int>> = LinkedList()
    q.add(start to 0)
    visited[start] = 1

    while (q.isNotEmpty()) {
        val (node, cnt) = q.poll()
        for (i in graph[node]) {
            if (visited[i] == 0) {
                visited[i] = 1
                q.add(i to cnt + 1)
                if (i == end) return cnt + 1
            }
        }
    }

    return -1
}

이 문제는 깊이(depth)를 고려해야하는 문제이다. 그러므로, Queue에 깊이를 나타내는 자료형도 추가하여 큐에 추가할 때마다 +1 하여 추가했다. 해당 문제는 노드에 연결된 다른 노드들을 리스트형태로 저장하여 위 문제와 다르게 행렬 그래프가 아니다.

---

알고리즘 개념 - 너비우선탐색(BFS)
[알고리즘] 너비 우선 탐색(BFS)이란