이 글을 잘 이해하기 위해서는 이진탐색트리, Balanced Tree, Tree의 순회에 대한 개념이 필요합니다.
이 글은 다음과 같은 순서로 되어 있습니다.
1. 왜 AVL 트리가 만들어졌고, 어떤 상황에서 필요한지에 대해 알아봅니다.
2. 데이터를 직접 삽입/삭제하며 AVL 트리가 어떻게 동작하는지를 확인합니다.
3. 실제 Java로 AVL 트리의 삽입과 삭제를 구현합니다.
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
상단 링크는 AVL 트리가 어떻게 모양이 변하는지 시각적으로 확인할 수 있는 사이트입니다. 스스로 AVL 트리를 만들고 데이터를 삽입하고 삭제하면서 제대로 만들고 있는지 아래 사이트를 통해 확인해보세요.
AVL트리가 만들어진 배경
이진탐색트리는 빠른 검색을 위해 사용되는 자료구조인데요. 데이터를 찾을 때 배열은 시간복잡도 O(N)을 갖지만, 이진탐색트리는 일반적인 상황에서 O(logN)이라는 시간복잡도를 가져 훨씬 효율적으로 검색할 수 있어요. 아래 이진탐색트리를 한 번 보겠습니다.
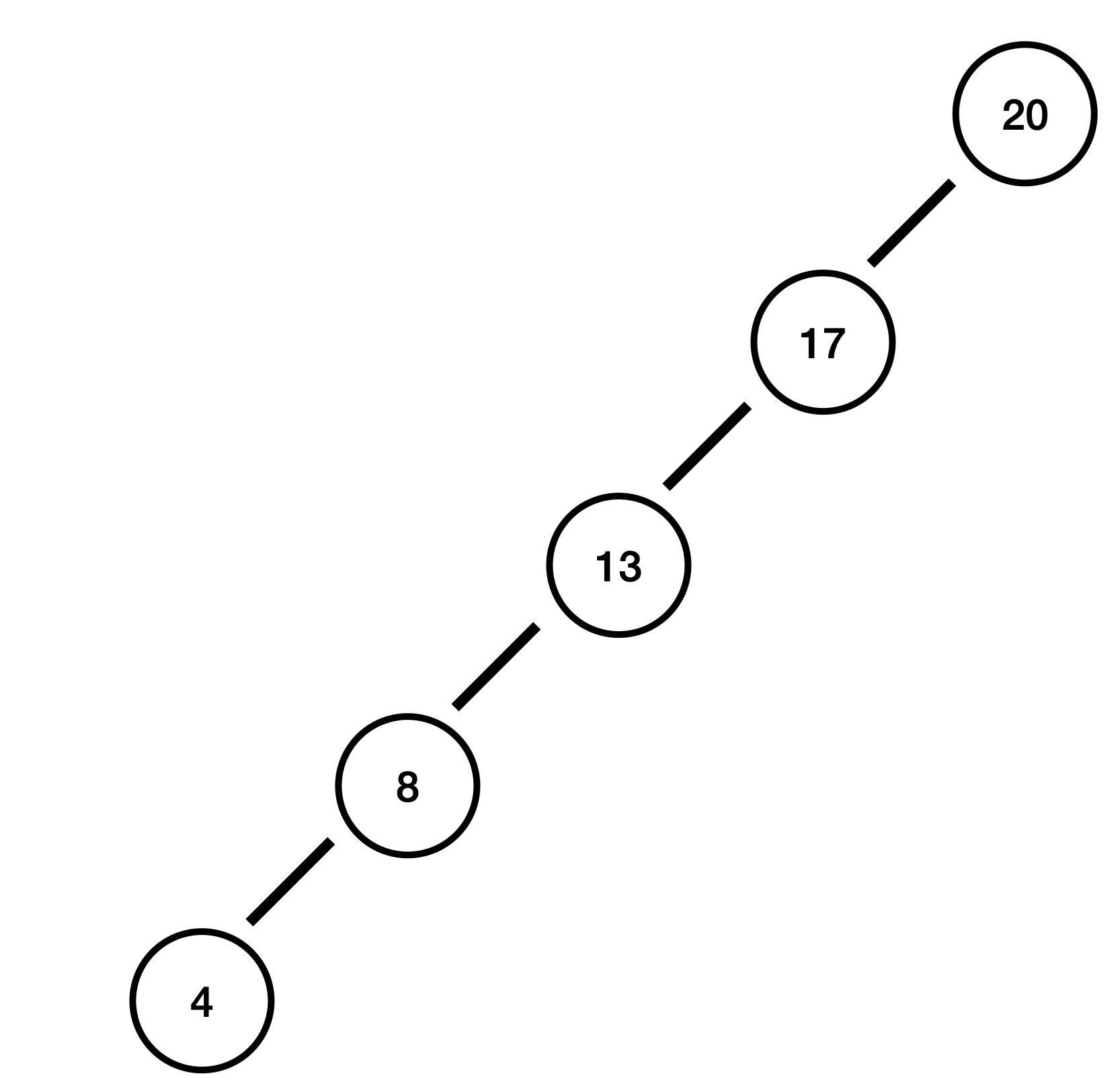
위 이진탐색트리에서 4라는 값을 찾아봅시다. 20에서부터 시작해서 17, 13, 8, 4 총 5개의 노드를 탐색해야 합니다. 이 경우 시간복잡도는 O(N)이 되는데요. 이게 바로 이진탐색트리의 약점입니다.
분명, 일반적인 상황에서는 O(logN)의 시간복잡도를 갖지만, 위와 같이 극단적인 상황에서는 O(N)이라는 시간복잡도를 갖게 됩니다.
즉, 트리가 위 예시처럼 편향되게 만들어지면 이진탐색트리는 검색에 있어서 효율적이지 못하다는 단점을 갖게 됩니다.
정리하면 이진탐색트리는 검색의 효율을 위해 편향되지 않은 Balanced Tree의 모양을 갖추고 있어야 합니다.
그래서 "데이터가 삽입/삭제될 때 트리 스스로 Balance를 맞출 수는 없을까?" 하는 아이디어에서 AVL 트리가 만들어졌습니다. AVL 트리는 그렇다면 어떻게 밸런스를 맞춰나갈까요?
정의
AVL 트리(발명자 Adelson-Velsky and Landis의 약자, 별 의미는 없다)는 트리 안의 모든 노드에서 왼쪽 Sub Tree, 오른쪽 Sub Tree의 높이 차이가 최대 1로만 되어 있는 트리입니다. 트리에 Data가 삽입되었을 때, 특정 노드에서 높이 차이가 1보다 커지면 스스로 균형을 잡으면서 Balance를 맞춰줍니다. 예시를 통해 어떻게 밸런스를 맞춰나가는지 이해를 해봅시다. 동영상으로 이해하는 게 편하시면 이 영상을 보시는걸 추천드릴게요.
예시
데이터가 삽입되는 예시
데이터가 삽입되는 경우 총 4가지의 Case가 존재합니다.
균형이 깨진 노드로부터 아래와 같은 4가지 경우가 가능해요.
1. 오른쪽-오른쪽
2. 왼쪽-왼쪽
3. 오른쪽-왼쪽
4. 왼쪽-오른쪽이 네 가지 경우들이 발생한 경우 어떻게 해결할 수 있는지 트리에 실제 데이터를 넣어보며 살펴보습니다.
❗️ 비어있는 노드는 자식이 존재하지 않는 리프 노드와 높이가 1이 차이나야 하므로, 비어있는 경우의 높이를 -1이라고 약속합니다. (리프 노드의 높이 == 0)
23삽입
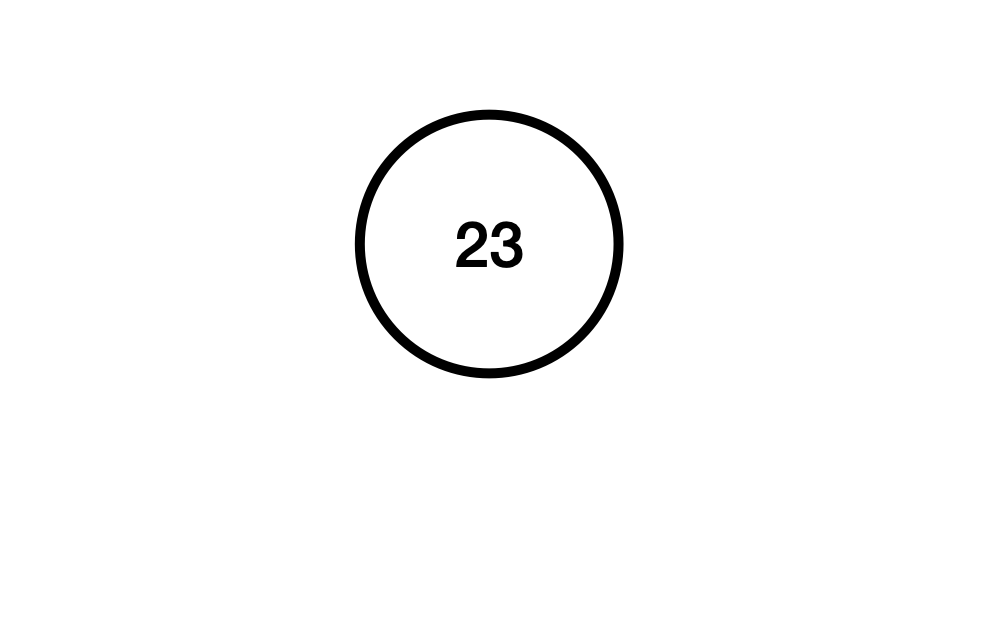
트리에 23을 삽입합니다. 트리의 Root가 없었기 때문에, 23은 Root가 됩니다.
23에서 왼쪽 Sub Tree와 오른족 Sub Tree의 높이 차는 0 -1 - (-1) = 0 으로 밸런스가 맞는 걸 확인할 수 있습니다.
50 삽입
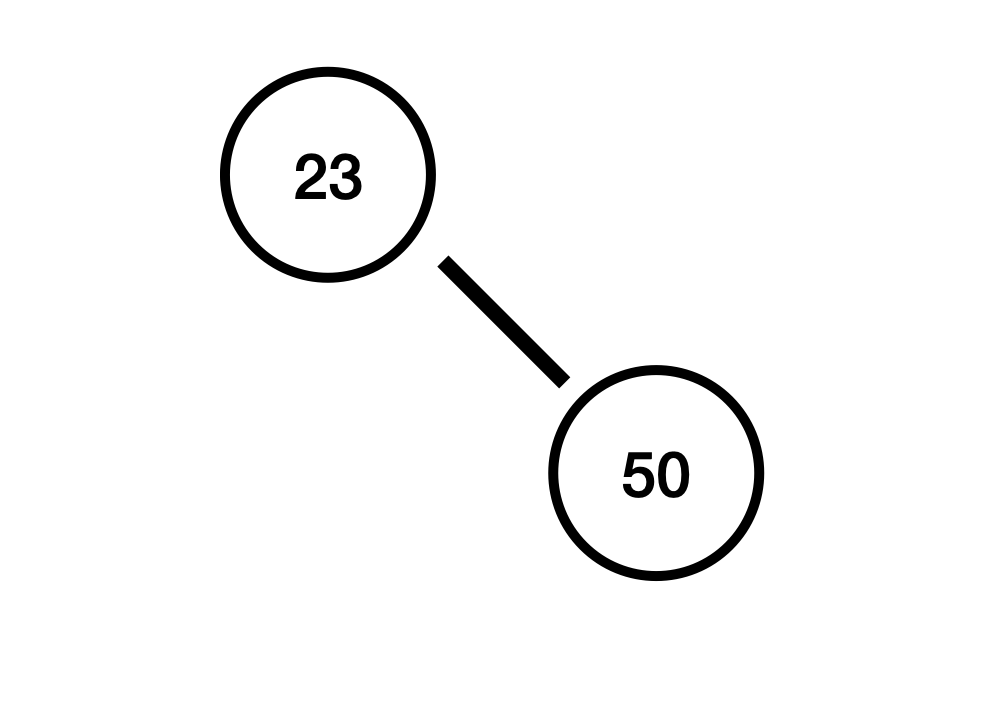
23 < 50 이기 때문에 노드 50은 23의 오른쪽으로 이동합니다. 23의 오른쪽 자식이 존재하지 않으므로 50은 23의 오른쪽 자식이 됩니다. 삽입된 노드를 기준으로 부모들이 밸런스가 깨지지 않았는지 확인합니다.
50에서 높이 차 : -1 - (-1) = 0
23에서 높이 차 : -1 - (0) = -1
❗️ 삽입된 노드를 기준으로, 부모들만 밸런스가 깨졌는지 확인하면 됩니다. 삽입된 노드의 조상이 아닌 경우 해당 노드를 기준으로 하단에 존재하는 노드들은 높이가 바뀔 일이 없습니다.
72 삽입 : 균형 깨짐!
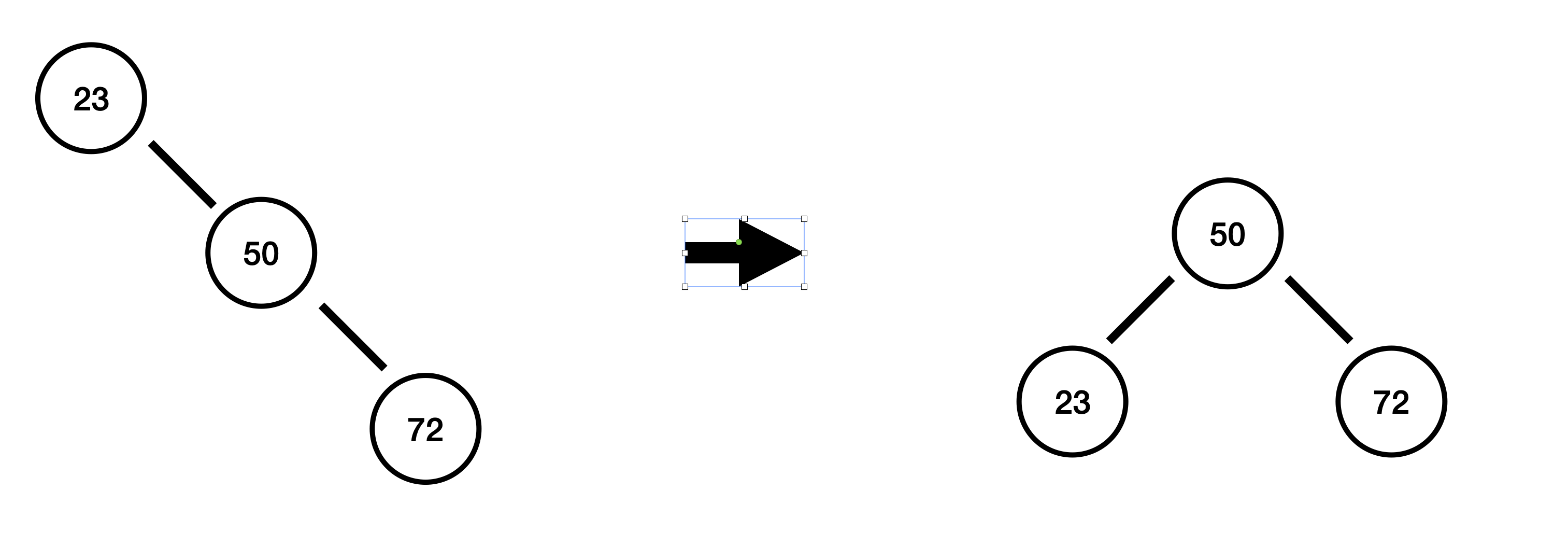
23 < 72 라서 23의 오른쪽으로 넘어옵니다. 해당 위치에는 50이 존재하는데, 50 < 72이기 때문에 오른쪽으로 이동한 뒤, 비어있는 자리이기 때문에 해당 위치로 72가 들어갑니다. 이 때 각 노드들의 높이를 계산해보겠습니다.
72에서 높이 차 : -1 - (-1) = 0
50에서 높이 차 : -1 - (0) = -1
23에서 높이 차 : -1 - (1) = -2 (균형 깨짐)
23에서는 높이 차이가 -2가 되는 걸 확인할 수 있습니다. 균형이 깨진 상황인데, 23을 기준으로 오른쪽 자식-오른쪽 자식 때문에 균형이 깨진 걸 확인할 수 있습니다. 이 경우에는 23을 기준으로 왼쪽 방향 회전을 시켜줍니다.
왼쪽 회전을 하게 되면 아래와 같은 과정을 거칩니다.
1. 오른쪽 자식 50이 해당 Sub Tree의 새로운 부모가 됩니다.
2. 원래 부모였던 23은 새로운 부모(노드 50)의 왼쪽 자식으로 들어간다.
3. 50의 왼쪽 자식은 23에게 자리를 뺏겼습니다. 그래서 새로운 자리에 넣어줘야 하는데, 그 위치는 자신의 자리를 뺏은 23의 오른쪽 자식이 됩니다.
❗️50의 왼쪽 자식이라는 건 무조건 23과 50 사이에 위치하게 됩니다. 그래서 50의 왼쪽 자식은 23의 오른쪽 자식으로 이동이 가능합니다.
17 삽입
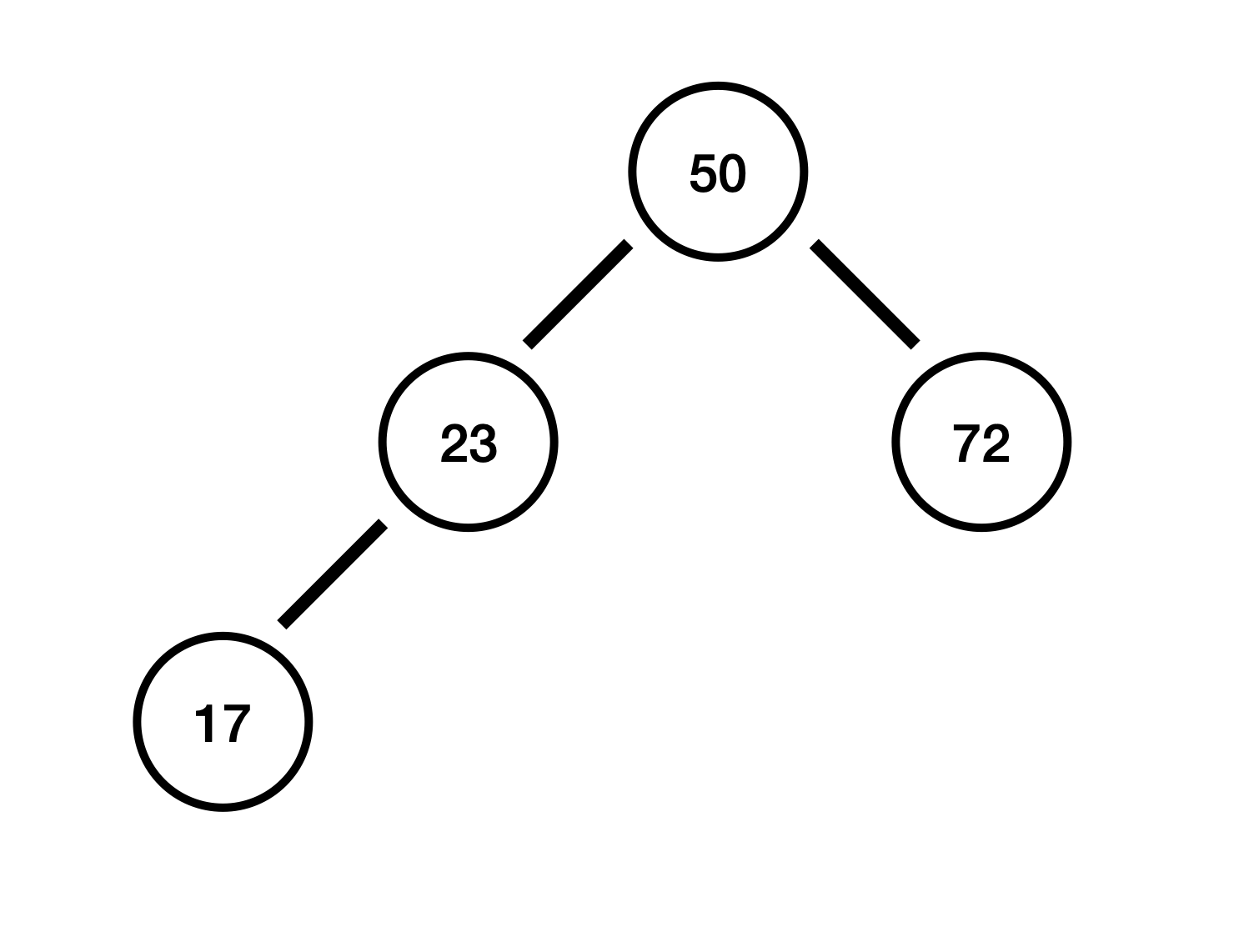
지금부터 노드가 어디 위치에 삽입되는지에 대한 설명은 생략하겠습니다. 삽입 이후 높이의 변화는 아래와 같습니다.
17에서 높이 차 : -1 - (-1) = 0
23에서 높이 차 : 0 - (-1) = 1
50에서 높이 차 : 1 - (0) = 1
12 삽입 : 균형 깨짐!
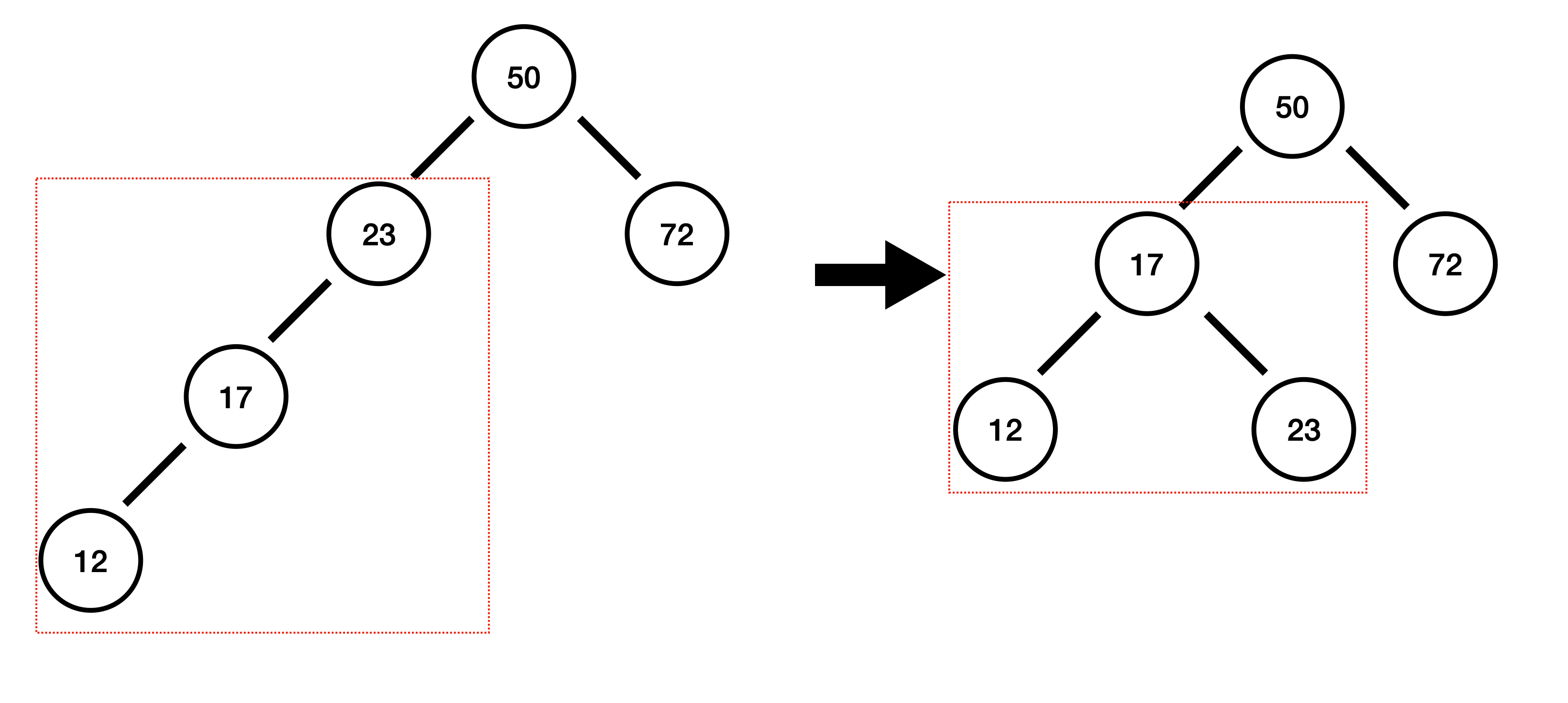
12에서 높이 차 : -1 - (-1) = 0
17에서 높이 차 : 0 - (-1) = 1
23에서 높이 차 : 1 - (-1) = 2 (균형 깨짐)
23에서 높이 차이가 2가 되면서 균형이 깨졌습니다. 23을 기준으로 왼쪽-왼쪽 형태로 균형이 깨져 있는데, 이 때는 23을 기준으로 오른쪽 방향 회전을 시켜줍니다.
오른쪽 회전을 하게 되면 아래와 같은 과정을 거칩니다.
1. 왼쪽 자식 17이 해당 Sub Tree의 새로운 부모가 됩니다.
2. 17의 오른쪽 자식으로 원래 부모였던 23이 들어갑니다.
3. 17의 오른쪽 자식은 23에게 자리를 뺏기기 때문에, 새로운 자리에 넣어줘야 한다. 자신의 자리를 뺏은 23의 왼쪽 자식으로 들어갑니다.
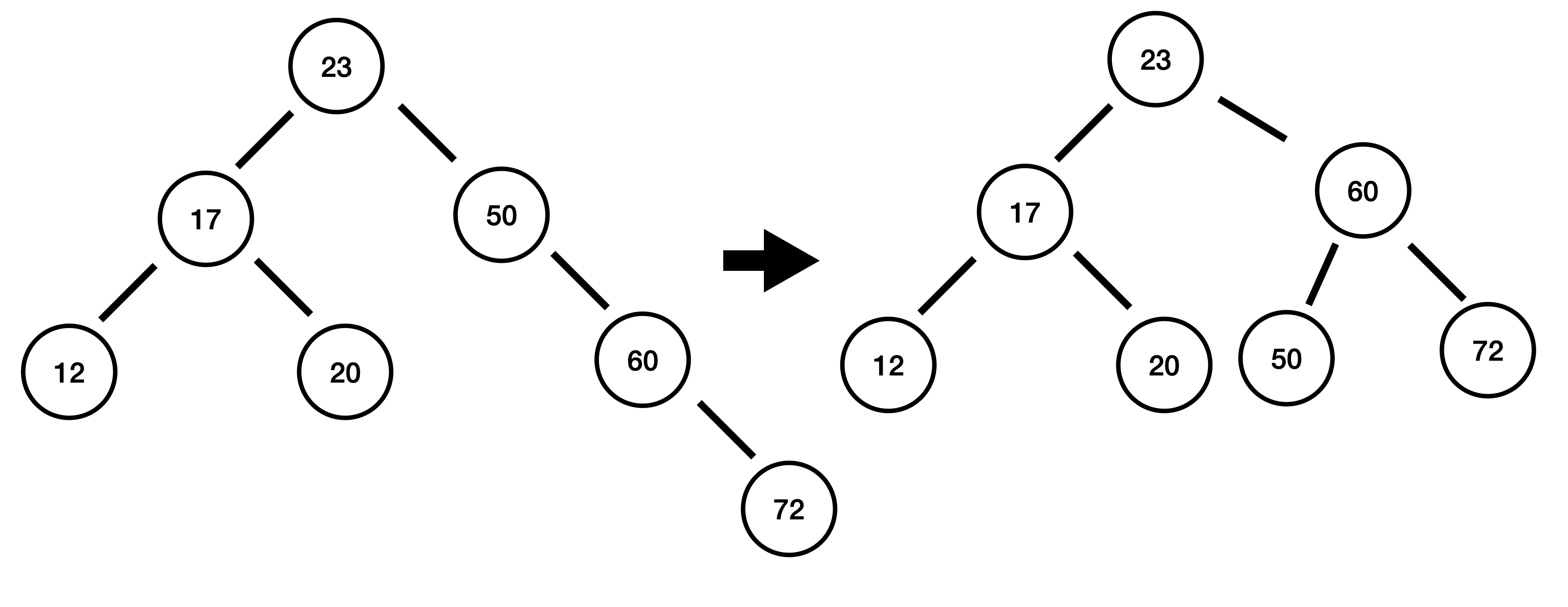
20 삽입 : 균형 깨짐!
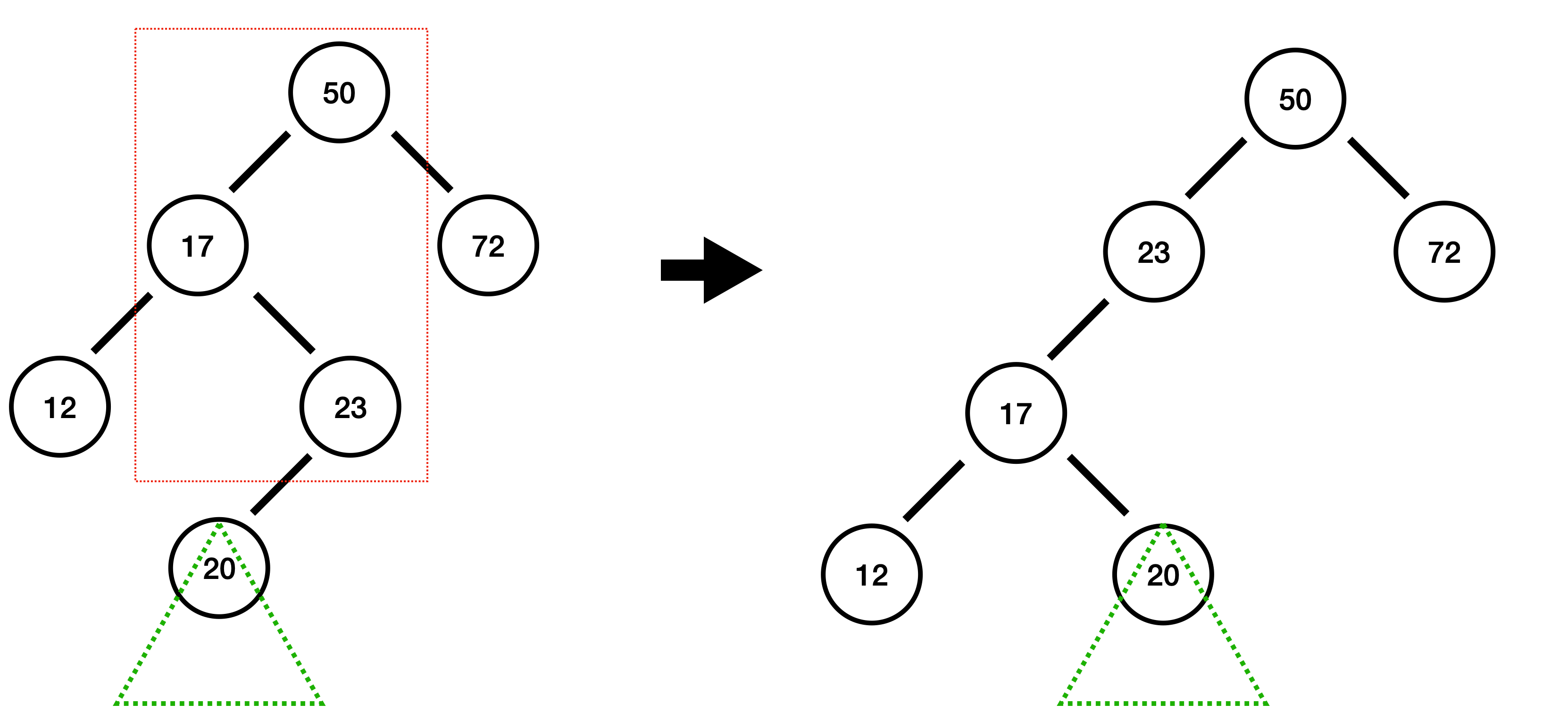
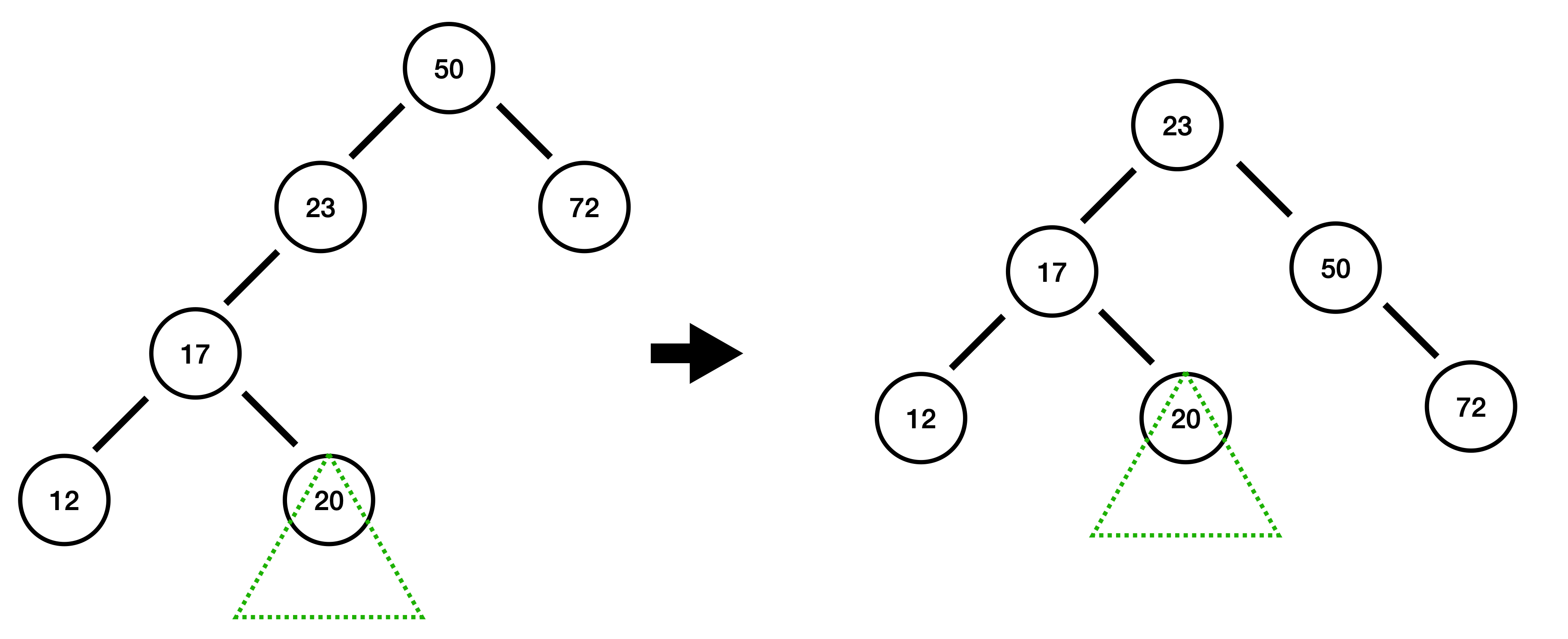
20에서 높이 차 : -1 - (-1) = 0
23에서 높이 차 : 0 - (-1) = 1
17에서 높이 차 : 0 - (1) = -1
50에서 높이 차 : 2 - (0) = 2 (균형 깨짐)
균형이 깨진 노드 50을 기준으로 왼쪽-오른쪽 형태로 균형이 깨져 있다. 이렇게 꺾인 모양으로 균형이 깨진 경우 먼저 꺾인 걸 펼쳐주는 과정이 필요합니다.
꺾인 모양을 펴주면 오른쪽-오른쪽 혹은 왼쪽-왼쪽으로 모양이 바뀌는데, 이전에 학습한 방식대로 균형을 잡아줍니다.
- 50의 자식 17을 기준으로 좌회전을 합니다.
- 원래 균형이 깨졌던 노드 50을 기준으로 우회전을 합니다.
60 삽입 : 균형 깨짐
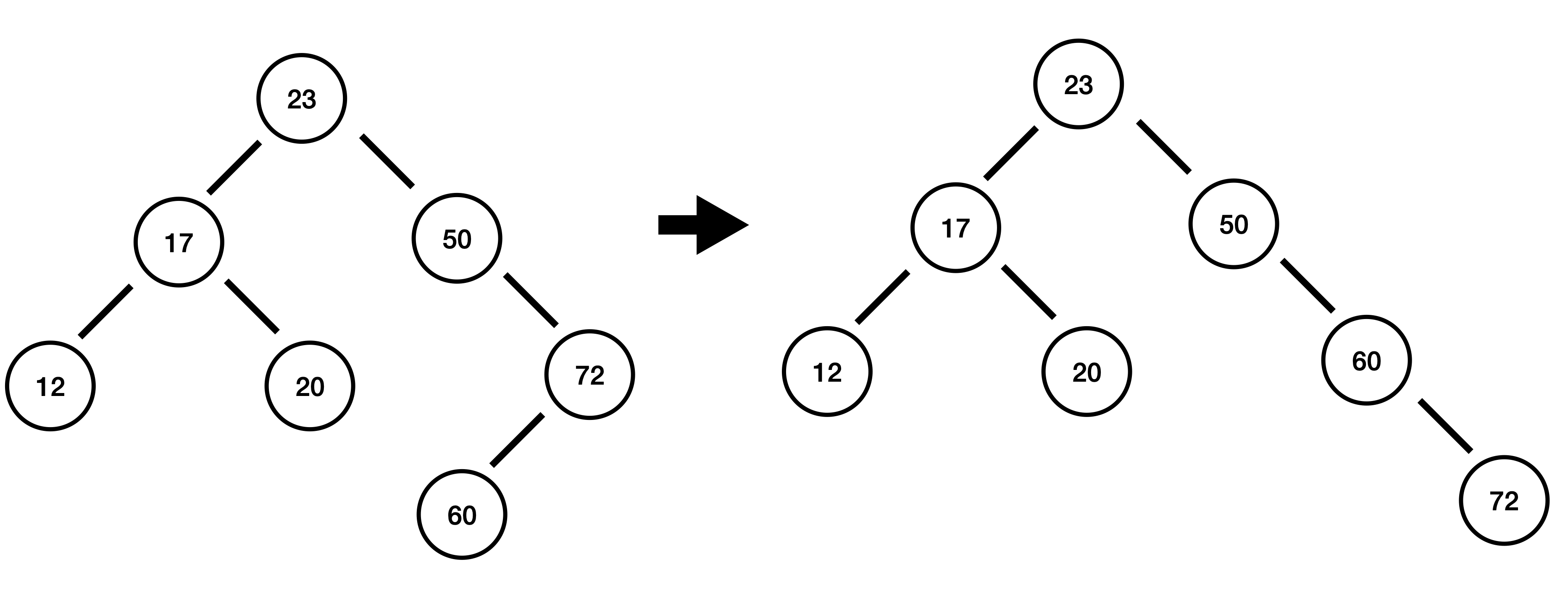
50에서 높이 차 : 0 - (2) = -2(균형 깨짐)
50 기준으로 오른쪽-왼쪽 형태로 균형이 깨진 Case인데, 아래 순서로 균형을 잡습니다.
- 50의 자식 72를 기준으로 우회전을 합니다.
- 50을 기준으로 좌회전을 합니다.
이렇게 네 가지 상황을 살펴보았는데, 이제 데이터가 삭제되는 예시를 보여드리겠습니다.
데이터가 삭제되는 예시
삭제되는 노드는 그냥 삭제되면 안됩니다. 삭제되는 노드는 누군가의 부모였을 수 있습니다. 부모가 그냥 사라진다면 자식들은 트리와 연결고리가 사라집니다. 그렇기 때문에 자신의 위치를 대체하는 다른 노드가 필요합니다.
삭제되는 노드는 자식의 개수에 따라 세 가지 타입으로 나눌 수 있습니다. 각 타입에 따라 해결하는 방식이 아래와 같이 달라집니다.
- 리프 노드 : 대체 하지 않고 그냥 삭제
- 자식이 1개 : 자식 노드가 삭제되는 노드를 대체
- 자식이 2개 : 좌측 Sub Tree의 최댓값 or 우측 Sub Tree의 최솟값이 삭제되는 노드를 대체
값을 삭제할 때, 트리에서 사라지는 노드의 위치는 해당 값을 대체한 노드의 원래 위치가 됩니다. 그래서 삭제되는 노드를 대체한 노드 를 기준으로 부모를 타고가며 밸런스가 깨졌는지 확인합니다. 밸런스가 깨지는 상황은 앞서 삽입할 때 알아보았으니 설명은 생략하겠습니다. 아래는 데이터를 삭제하는 예시입니다.
50 삭제
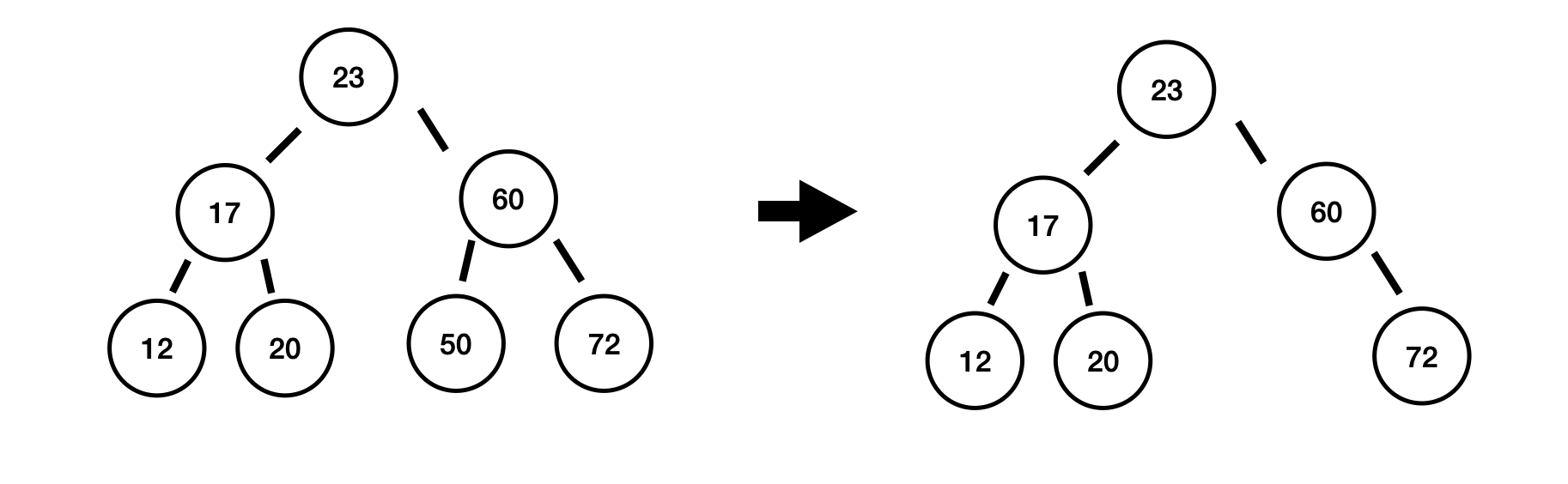
50은 리프 노드이기 때문에 대체할 필요 없이 해당 위치에서 삭제가 일어납니다.
삭제된 50의 부모부터 부모를 타고가며 검사한다.
60에서 높이 차 : -1 - (0) = -1
23에서 높이 차 : 1 - (1) = 0
23 삭제
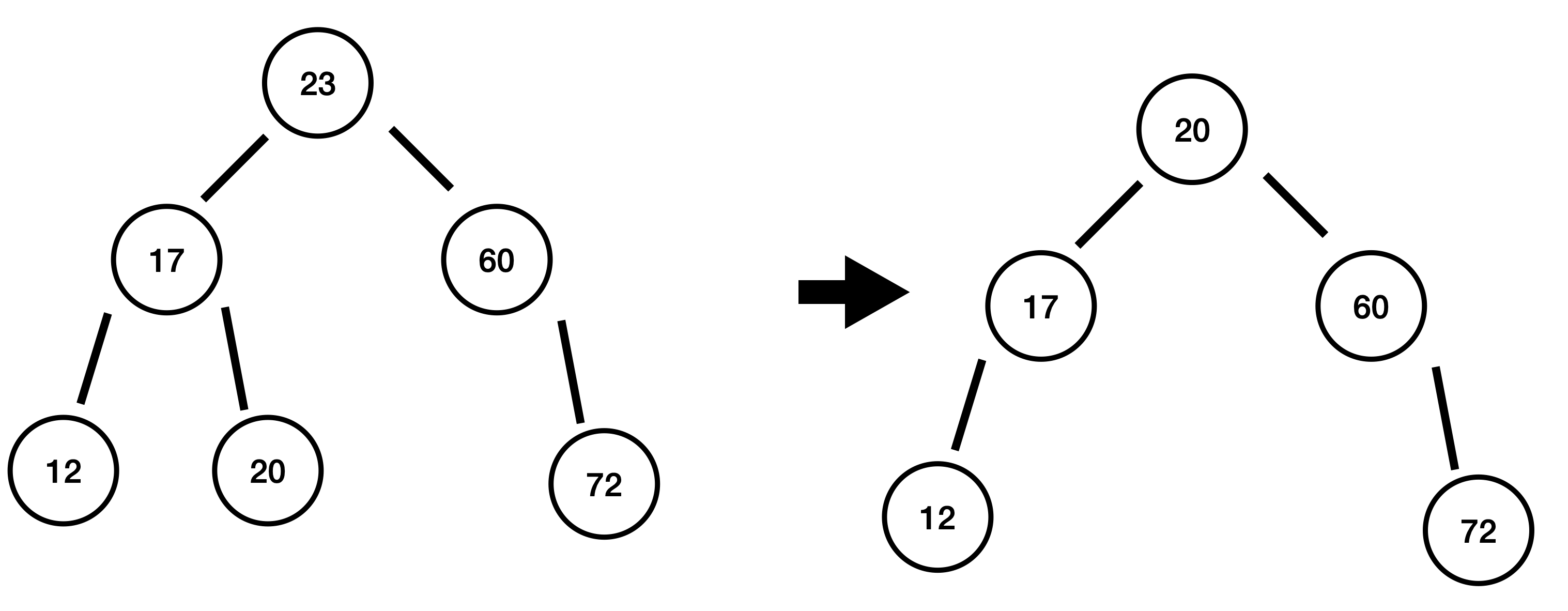
23은 왼쪽, 오른쪽에 모두 자식이 존재합니다. 왼쪽 Sub Tree의 최댓값 20을 통해 삭제되는 노드 23의 위치를 대체합니다.
위 사진에서 실제 사라지는 노드의 위치는 20이 존재하던 위치이기 때문에 20을 기준으로 높이의 변화가 생기게 됩니다. 그래서 20부터 부모를 타고 오면서 밸런스가 깨졌는지를 검사합니다.
17에서 높이 차 : 0 - (-1) = 1
20에서 높이 차 : 1 - (1) = 0
60 삭제
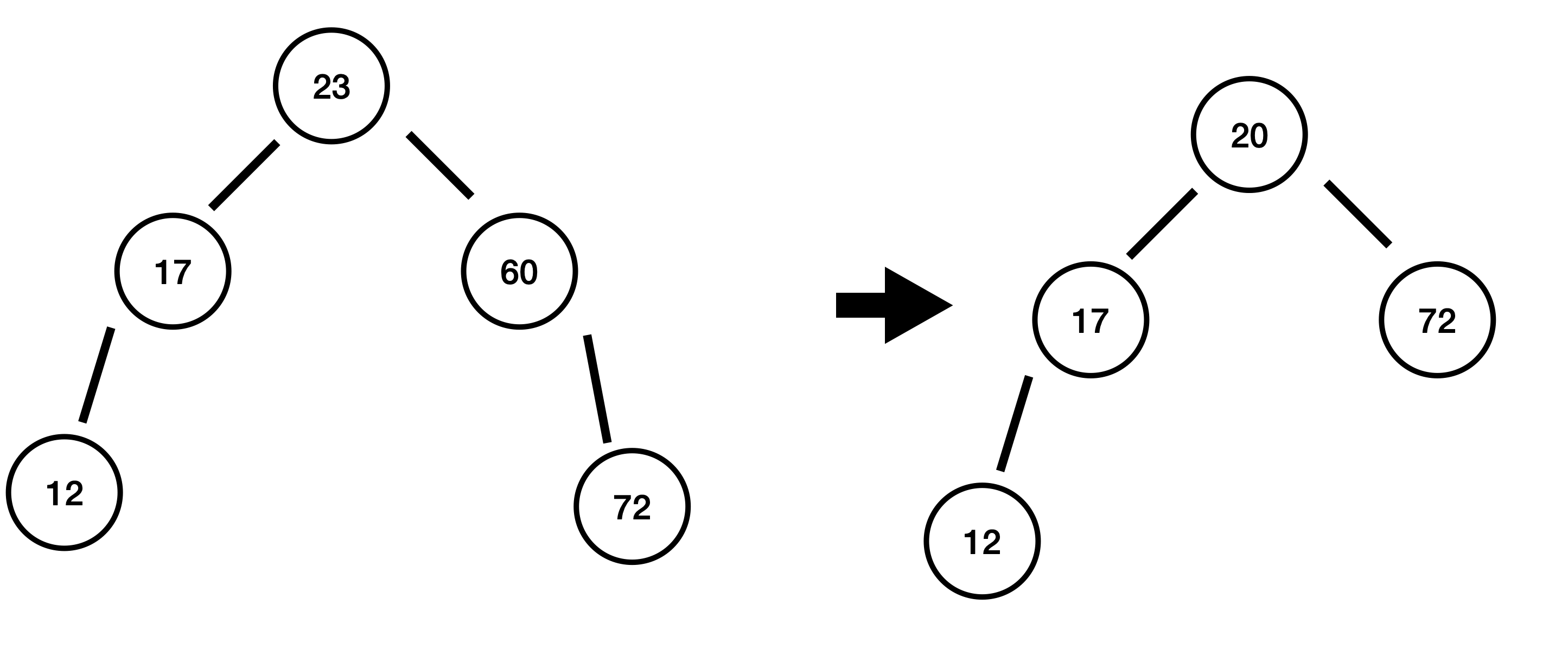
60은 자식이 하나만 존재합니다. 그래서 60의 자식 72가 60의 위치를 대체합니다. 이후 원래 72의 부모부터 밸런스가 깨졌는지를 검사합니다.
72에서 높이 차 : -1 - (-1) = 0
20에서 높이 차 : 1 - (0) = 1
72 삭제
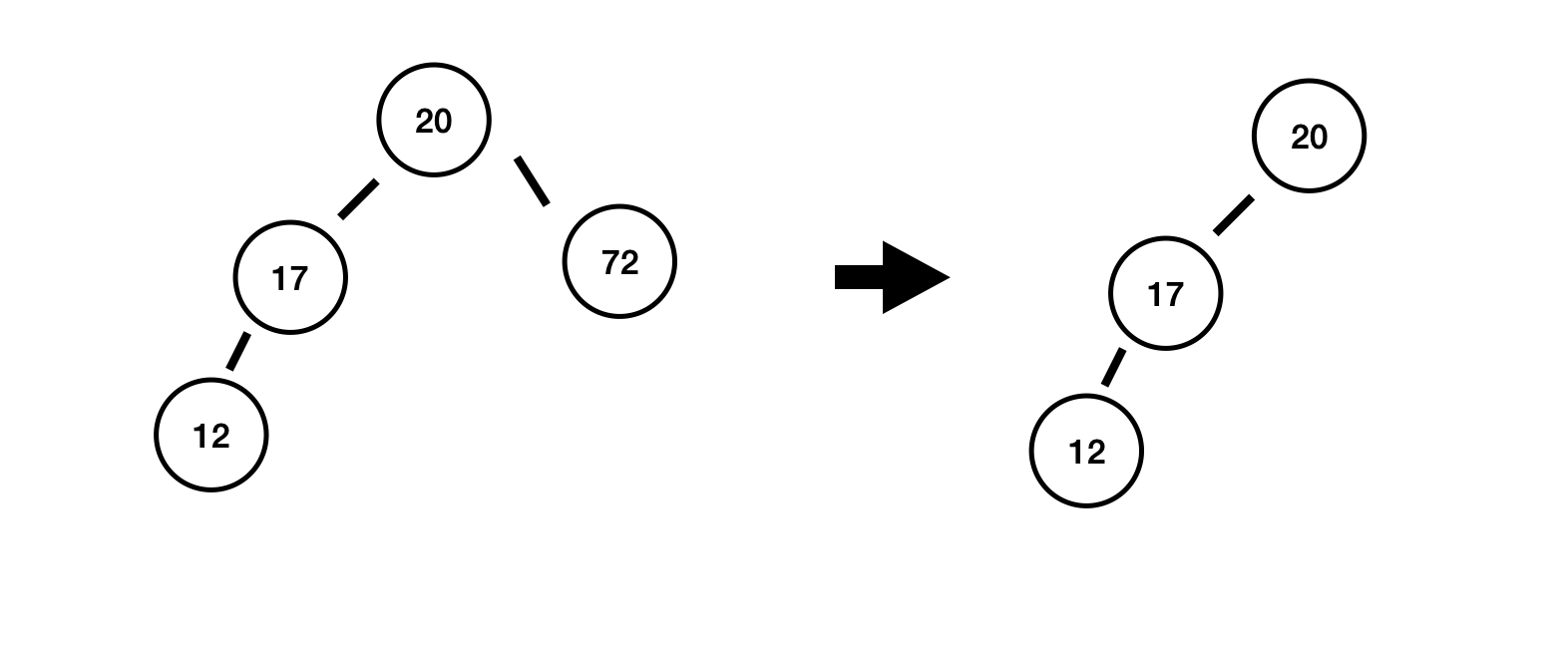
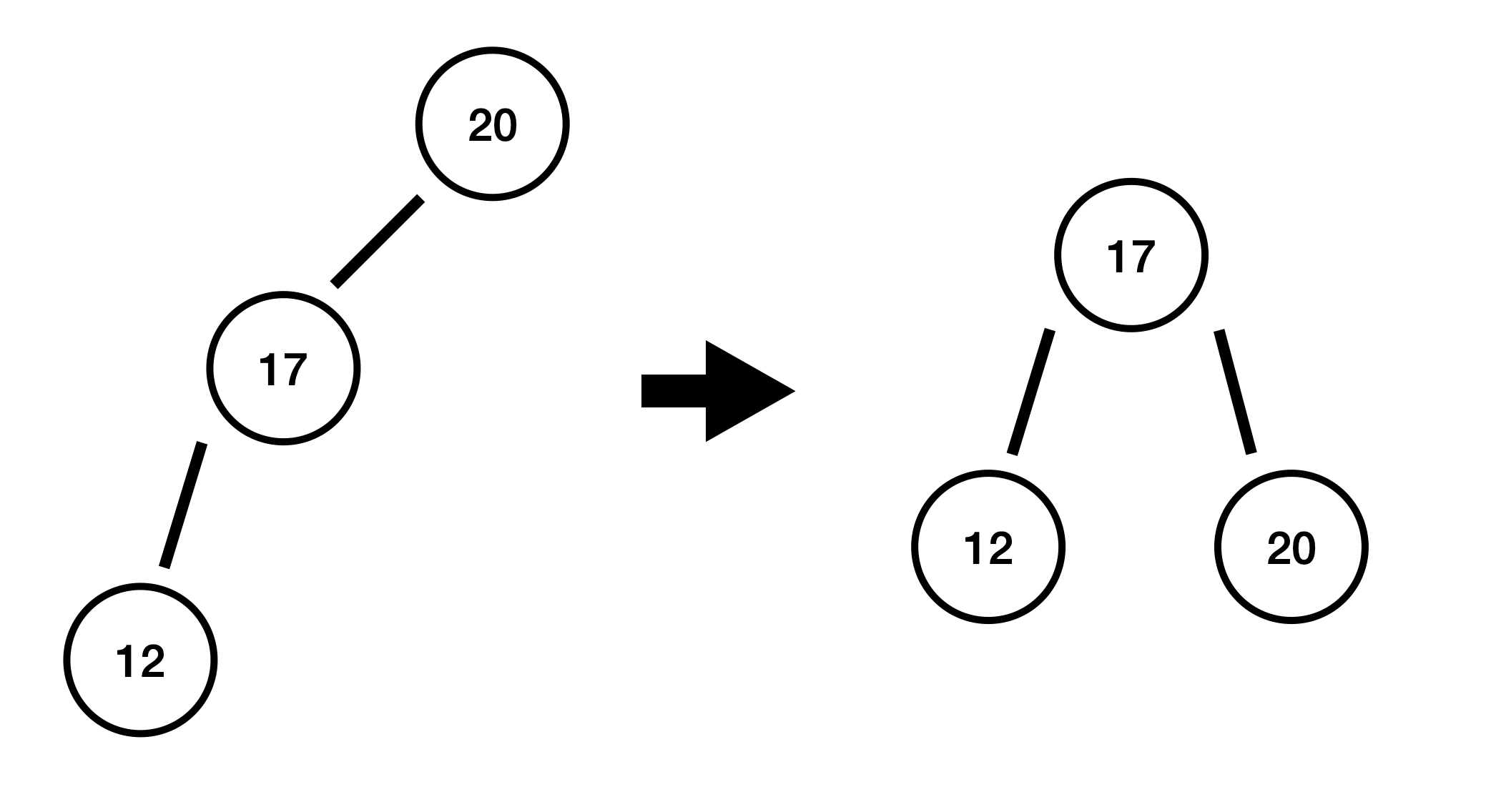
20에서 높이 차 : 2 - 0 = 2 (균형 깨짐)
왼쪽-왼쪽으로 편향되었기 때문에 우회전을 시켜줍니다.
이렇게 삭제가 일어났을 때 균형이 깨지는 상황에 대해서도 알아보았습니다. 이해가 되지 않았다면 다시 한 번 종이에 그림을 그려보며 글을 따라오는 걸 추천하겠습니다.
균형이 깨지는 Case 정리
데이터가 삽입/삭제될 때 트리의 균형이 깨진다면, 아래 네 가지 경우의 수가 존재합니다.
첫 번째 경우의 수는 균형이 깨진 노드를 기준으로 균형이 오른쪽-오른쪽 방향으로 깨진 케이스입니다.
- (오른쪽) 자식 노드는 새로운 부모가 된다.
- 원래 부모는 (오른쪽) 자식 노드의 (왼쪽) 자식 노드가 된다.
- (오른쪽) 자식 노드의 (왼쪽) Sub Tree는 원래 부모의 (오른쪽) Sub Tree가 된다.
두 번째 경우의 수는 왼쪽-왼족 방향으로 균형이 깨진 케이스인데, 해당 케이스는 위의 예시에서 괄호 안에 있는 값을 반대로 바꾸어 생각하면 됩니다.
세 번째 경우의 수는 오른쪽-왼쪽으로 트리의 균형이 깨진 케이스입니다. 해당 경우는 아래와 같이 해결할 수 있습니다.
- (오른쪽) 자식 노드를 기준으로 (왼쪽) 방향 회전을 한다.
- 원래 부모를 기준으로 (오른쪽)-(오른쪽) 형태로 트리 모양이 변경되는데, 해당 방향에서 해결할 수 있다.
네 번째 경우의 수는 왼쪽-오른쪽으로 트리의 균형이 깨진 케이스인데, 마찬가지로 오른쪽-왼쪽 균형이 깨진 예시에서 괄호 안의 값을 반대로 바꿔주면 됩니다.
구현
AVL 트리에 대한 이해가 끝났다면, 실제 코드로 구현해보며 실력을 키워봅시다.
Insert 구현
Tree 인터페이스
우선 Tree의 인터페이스를 만들어보겠습니다.
Tree에 필요한 기능은 아래와 같습니다.
- 데이터를 삽입/삭제
- 트리를 순회하며 데이터를 조회
package tree;
interface Tree {
public void insert(Integer data);
public void delete(Integer data);
public void traverse(); // 순회
}
노드
트리를 만들기 전, 트리의 구성요소인 노드를 만들겠습니다. 노드에 필요한 필드는 다음과 같습니다.
- 입력한 데이터를 저장하기 위한
data - 왼쪽, 오른쪽 자식 노드를 저장하기 위한
left,right - 각 SubTree의 높이를 비교하는데 사용하는
height
노드의 초기 높이는 0입니다. 노드가 아무런 처리도 되지 않았다는 건 left, right 자식 노드가 없다는 뜻이 됩니다.
class Node {
Integer data;
Node left;
Node right;
int height;
public Node(Integer data) {
this.data = data;
height = 0;
}
}AVL Tree 구현
AVL Tree는 우선 root 노드를 저장해야 합니다. root 노드에서 시작해 노드들을 연결시키기 때문입니다.
그리고 균형을 맞추기 위해 각 노드의 높이를 리턴하는 메서드 역시 필요합니다.
아래 예시에서는 전위 순회 방식으로 트리를 조회할 생각입니다.
package tree;
public class AVL implements Tree {
private Node root;
// 위에서 node가 없을 때 높이는 -1이라고 약속했다.
int height(Node node) {
if (node == null)
return -1;
return node.height;
}
@Override
public void insert(Integer data) {
}
@Override
public void delete(Integer data) {
}
@Override
public void traverse() {
if (this.root != null) {
traverse(this.root);
} else {
System.out.println("해당 트리는 비어있습니다.");
}
}
private void traverse(Node node) {
// preorder
if (node != null) {
System.out.print(node.data);
if (node.left != null) {
System.out.print(" // left node -> "+node.left.data);
} else {
System.out.print(" // left node -> null");
}
if (node.right != null) {
System.out.print(" // right node -> "+node.right.data);
} else {
System.out.print(" // right node -> null");
}
System.out.println();
traverse(node.left);
traverse(node.right);
}
}
}❓왜 traverse 메서드는 traverse()와 traverse(node)로 오버로딩 되어있을까?
traverse 메서드는 재귀 방식으로 일어납니다. traverse(parent)를 호출하면 traverse(왼쪽자식) traverse(오른쪽자식)을 실행하는 과정으로 데이터를 순회합니다.
즉, traverse(node)라는 메서드가 필요한데 해당 메서드가 Public으로 되어 있을 경우 사용자는 아무런 노드에서 traverse 메서드를 실행시킬 수 있다.
traverse(node)를 Private으로 감추고, Public한 traverse() 메서드를 만들어주면 사용자는 traverse() 메서드만 사용할 수 있습니다. traverse()를 실행하면 traverse(root)가 실행되도록 만들어줍니다. 이제 사용자는 Root 노드에서만 traverse를 실행시킬 수 있게 됩니다.
정리하면 사용자가 임의의 메서드에 접근하지 못하도록 만들기 위해 위와 같은 방식을 사용합니다. 해당 방식은 insert, delete에서도 똑같이 적용될 예정입니다.
이제 Tree의 삽입 메서드를 만들어보겠습니다. 앞서 설명했던 것처럼 insert 메서드를 오버로딩합니다.
@Override
public void insert(Integer data) {
this.root = insert(this.root, data);
}
private Node insert(Node node, Integer data) {
}AVL Tree 역시 이진탐색트리이기 때문에 현재 노드보다 작은 값이 들어오면 왼쪽, 큰 값이 들어오면 오른쪽에 노드를 추가합니다. 이미 존재하는 값이라면 아무 노드를 추가하지 않습니다. 삽입 결과로 해당 SubTree의 root를 반환합니다.
private Node insert(Node node, Integer data) {
if (node == null) {
return new Node(data);
}
if (data < node.data) {
node.left = insert(node.left, data);
} else if (data > node.data) {
node.right = insert(node.right, data);
}
return node;
}
이렇게 이진탐색트리가 만들어졌습니다. 만들어진 트리를 실행하면 아래와 같은 결과가 출력됩니다.
public class Main {
public static void main(String[] args) {
// 현재 코드 : 이진탐색트리 예시
AVL tree = new AVL();
tree.insert(10);
tree.insert(20);
tree.insert(30);
tree.insert(40);
tree.insert(50);
tree.insert(25);
tree.traverse();
}
}
// return value는 아래와 같습니다.
// 10 // left node -> null // right node -> 20
// 20 // left node -> null // right node -> 30
// 30 // left node -> 25 // right node -> 40
// 25 // left node -> null // right node -> null
// 40 // left node -> null // right node -> 50
// 50 // left node -> null // right node -> null
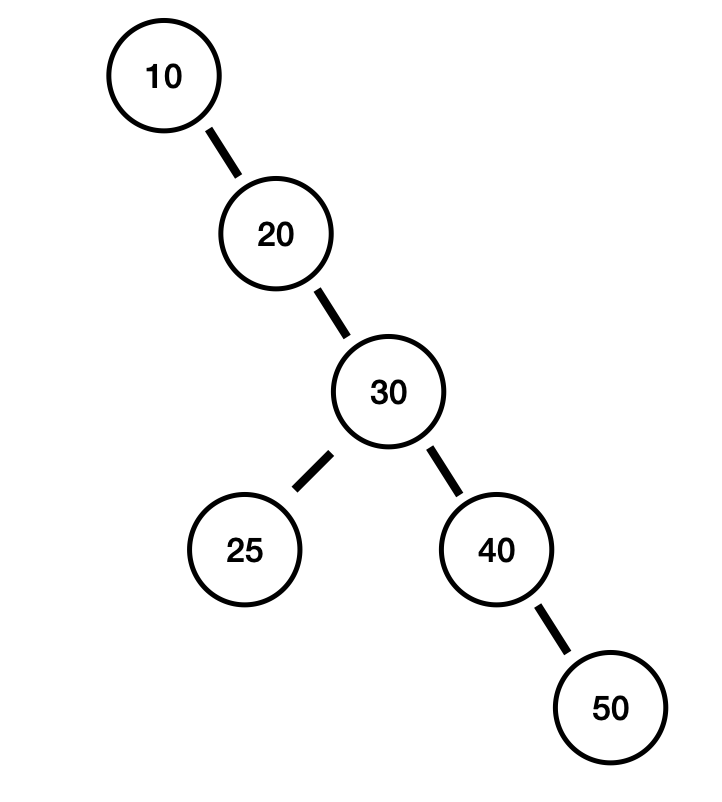
이진탐색트리를 만들었습니다! 하지만 우리가 만들어야 하는 건 AVL 트리입니다.
AVL 트리는 균형이 깨진 걸 인지하고 회전을 돌릴 수 있어야 합니다.
앞서 살펴본 좌회전시 발생하는 로직을 가져오겠습니다.
- 오른쪽 자식 노드는 새로운 부모가 된다.
- 원래 부모는 오른쪽 자식 노드의 왼쪽 자식 노드가 된다.
- 오른쪽 자식 노드의 왼쪽 Sub Tree는 원래 부모의 오른쪽 Sub Tree가 된다.
한 번 차근차근 구현해 볼까요?
1. 오른쪽 자식 노드는 새로운 부모가 된다.
오른쪽 자식 노드를 newParent라는 변수에 저장합니다.
2. 원래 부모는 오른쪽 자식 노드의 왼쪽 자식 노드가 된다.
newParent의 left에 parent를 저장합니다.
3. 오른쪽 자식 노드의 왼쪽 Sub Tree는 원래 부모의 오른쪽 Sub Tree가 된다.
오른쪽 자식 노드의 왼쪽 Sub Tree를 T2에 저장한 뒤, 원래 부모의 오른쪽 자식으로 T2를 할당합니다.
코드는 아래와 같습니다.
private Node leftRotate(Node parent) {
// 오른쪽 자식 노드를 ```newParent```라는 변수에 저장한다.
Node newParent = parent.right;
// 오른쪽 자식 노드의 왼쪽 Sub Tree를 T2에 저장한다.
Node T2 = newParent.left;
// newParent의 left에 parent를 저장한다.
newParent.left = parent;
// 원래 부모의 오른쪽 자식으로 T2를 할당한다
parent.right = T2;
// 회전 이후 트리의 부모를 반환한다(부모를 통해서 전체 트리에 연결되니까)
return newParent;
}자식 노드가 바뀌면 부모 노드는 높이가 변경될 수 있습니다.
노드의 높이 = max(왼쪽 자식 높이, 오른쪽 자식 높이) + 1
회전이 일어난 뒤, 자식 노드가 변경된 노드들은 parent와 newParent입니다. 따라서 이 두 노드에서 새롭게 높이를 계산해야 합니다.
❗️ 주의할 점은 parent의 높이를 먼저 계산해줘야 한답니다. 왜냐하면 부모 높이 = max(자식1, 자식2) + 1 이기 때문입니다. 아래 코드에서는 newParent의 높이는 max(parent의 높이, 다른 자식의 높이) + 1 입니다. parent 높이의 갱신 없이 newParent의 높이를 갱신하면 제대로 된 높이가 나오지 않겠죠?
Node들의 높이를 새롭게 계산해준 코드는 아래와 같습니다.
// 좌회전
private Node leftRotate(Node parent) {
Node newParent = parent.right;
Node T2 = newParent.left;
newParent.left = parent;
parent.right = T2;
parent.height = Math.max(height(parent.left), height(parent.right)) + 1;
newParent.height = Math.max(height(newParent.left), height(newParent.right)) + 1;
return newParent;
}우회전 역시 같은 논리흐름이기 때문에 설명은 생략하겠습니다.
private Node rightRotate(Node parent) {
Node newParent = parent.left;
Node T2 = newParent.right;
newParent.right = parent;
parent.left = T2;
parent.height = Math.max(height(parent.left), height(parent.right)) + 1;
newParent.height = Math.max(height(newParent.left), height(newParent.right)) + 1;
return newParent;
}좌회전, 우회전을 만들었으니 이제 insert를 완성시켜볼까요?
트리에 데이터를 삽입한 뒤, 데이터가 삽입된 부분부터 높이를 갱신하며 해당 노드의 밸런스가 깨졌는지를 확인합니다.
만약 밸런스가 깨졌다면 네 가지 상황을 구별해 회전을 시켜줍니다.
이렇게 완성된 Insert 코드는 아래와 같습니다.
private Node insert(Node node, Integer data) {
// BST 삽입을 수행
// 트리의 첫 값이 삽입되었을 때 새로운 노드를 만든다 -> 해당 노드는 root가 된다
if (node == null) {
return new Node(data);
}
if (data < node.data) {
node.left = insert(node.left, data);
} else if (data > node.data) {
node.right = insert(node.right, data);
} else {
// 변경되는 코드가 없으니 Early Return을 시킨다.
return node;
}
// 데이터가 삽입된 이후, 높이를 갱신한다
node.height = 1 + Math.max(height(node.left), height(node.right));
int balance = getBalance(node);
// left-left
if (balance > 1 && data < node.left.data)
return rightRotate(node);
// right-right
if (balance < -1 && data > node.right.data) {
return leftRotate(node);
}
// left-right
if (balance > 1 && node.left.data < data) {
node.left = leftRotate(node.left); // 왼쪽 자식노드에 대해 먼저 좌회전을 한다
return rightRotate(node);
}
// right-left
if (balance < -1 && data < node.right.data) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 데이터가 삽입되었지만, 밸런스가 깨지지 않은 경우
return node;
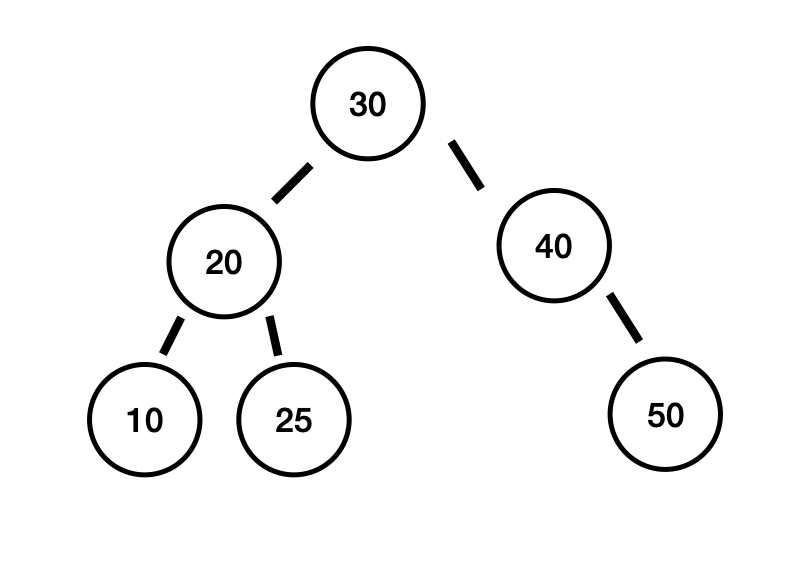
}다시 예시 코드를 넣어보면 아래와 같이 결과가 바뀝니다.
public class Main {
public static void main(String[] args) {
// 현재 코드 : 이진탐색트리 예시
AVL tree = new AVL();
tree.insert(10);
tree.insert(20);
tree.insert(30);
tree.insert(40);
tree.insert(50);
tree.insert(25);
tree.traverse();
}
}
// return value는 아래와 같습니다.
// 30 // left node -> 20 // right node -> 40
// 20 // left node -> 10 // right node -> 25
// 10 // left node -> null // right node -> null
// 25 // left node -> null // right node -> null
// 40 // left node -> null // right node -> 50
// 50 // left node -> null // right node -> null
위 예시를 실행하면 아래와 같은 트리를 보여줍니다.
Delete 구현
삭제 역시 이진탐색트리와 마찬가지로 구현합니다. 삭제할 값이 현재 노드보다 작으면 왼쪽, 크면 오른쪽 자식으로 이동합니다. delete의 결과로 해당 SubTree의 root를 반환합니다.
삭제 연산 시 삭제할 값을 발견하면 삭제하는 과정이 필요합니다.
삭제하는 노드가 존재하면, 아래와 같은 과정이 필요합니다.
- 해당 노드의 자식이 존재하는지 확인한다.
- 만약 자식이 존재한다면 대체할 노드를 찾는다.
2-1. 왼쪽 자식이 존재한다면, 왼쪽 자식의 Tree에서 최댓값을 찾는다.(자식이 1개일수도 2개일수도 있다.)
2-2. 왼쪽 자식이 존재하지 않는다면(자식은 1개), 해당 노드를 대체하는 노드는 오른쪽 자식이 된다.- 자식이 존재하지 않으면 해당 노드를 삭제한다(== 해당 서브트리를 삭제한다)
- 삭제 이후 밸런스가 깨졌으면 회전을 돌린다.
자식이 존재하지 않는다면 null을 반환합니다. null을 반환한다는 건 해당 delete 메서드를 호출한 부모의 parent.left 혹은 parent.right가 null이 된다는 의미입니다. 즉, parent와 연결을 끊음으로써 자신을 삭제합니다.
삭제할 노드의 왼쪽 자식이 존재하지 않는다면, 자식이 한 개이기 때문에 오른쪽 자식으로 자신을 대체합니다. 오른쪽 자식을 해당 SubTree의 Root로 만들어 반환합니다. 즉, delete 메서드를 호출한 부모에게 오른쪽 자식을 반환해 자신을 삭제하고 부모와 오른쪽 자식을 연결합니다.
왼쪽에 자식이 존재하면 왼쪽 서브 트리의 최댓값을 찾습니다. 발견한 노드를 삭제하고, 자신의 값을 왼쪽 서브 트리의 최댓값으로 변경합니다.
private Node delete(Node node, Integer data) {
if (node == null) {
return null;
}
// 삭제할 값을 찾는 중
if (data < node.data) {
node.left = delete(node.left, data);
} else if (data > node.data) {
node.right = delete(node.right, data);
}
else {
// 삭제할 값 발견 -> 대체할 노드를 찾아야 한다.
// 자식의 개수에 따라서 삭제된 노드를 대체하는 노드가 달라진다 (자식 입장에서 부모를 찾을 수 없음 -> 그래서 값을 바꾸는 방식을 사용)
if (node.getChildCnt() == 0) {
node = null;
} else {
if (node.left != null) { // 좌측 subtree에서 가장 큰 값을 찾는다(left에 자식이 있음)
Node target = findMaxNode(node.left);
node.data = target.data;
node.left = delete(node.left, target.data);
} else { // 자식이 1개(right에만) -> 자식을 자신의 위치로 올리면 된다
node = node.right;
}
}
}
return node;
}
private Node findMaxNode(Node node) {
// max Value를 찾고,
if (node.right != null) {
return findMaxNode(node.right);
} else {
return node;
}
}
삭제를 끝마친 뒤 높이를 재조정하고 밸런스가 깨진 경우 회전을 시킵니다. 삽입과 동일한 연산이 수행되어 설명은 생략하겠습니다.
private Node delete(Node node, Integer data) {
if (node == null) {
return null;
}
// 삭제할 값을 찾는 중
if (data < node.data) {
node.left = delete(node.left, data);
} else if (data > node.data) {
node.right = delete(node.right, data);
}
else {
// 삭제할 값 발견 -> 대체할 노드를 찾아야 한다.
// 자식의 개수에 따라서 삭제된 노드를 대체하는 노드가 달라진다 (자식 입장에서 부모를 찾을 수 없음 -> 그래서 값을 바꾸는 방식을 사용)
if (node.getChildCnt() == 0) {
node = null;
} else {
if (node.left != null) { // 좌측 subtree에서 가장 큰 값을 찾는다(left에 자식이 있음)
Node target = findMaxNode(node.left);
node.data = target.data;
node.left = delete(node.left, target.data);
} else { // 자식이 1개(right에만) -> 자식을 자신의 위치로 올리면 된다
node = node.right;
}
}
}
if (node == null) { // Leaf노드가 삭제된 케이스
return null;
}
// 높이를 다시 정의한다
// node에서 밸런스가 깨지지 않았는지 검사한다
node.height = Math.max(height(node.left),height(node.right)) + 1;
int balance = getBalance(node);
if (node.left != null) {
System.out.println(node.left.data);
}
// left-left
if (balance > 1 && data < node.left.data) {
return rightRotate(node);
}
// right-right
if (balance < -1 && data > node.right.data) {
return leftRotate(node);
}
// left-right
if (balance > 1 && node.left.data < data) {
node.left = leftRotate(node.left); // 왼쪽 자식노드에 대해 먼저 좌회전을 한다
return rightRotate(node);
}
// right-left
if (balance < -1 && data < node.right.data) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 변경사항이 없을 경우
return node;
// 밸런스가 깨지지 않았는가 검사한다
}
private Node findMaxNode(Node node) {
// max Value를 찾고,
if (node.right != null) {
return findMaxNode(node.right);
} else {
return node;
}
}
삭제까지 모든 코드가 완성되었습니다. 참고로 삭제 연산의 경우 대체할 노드를 찾는 과정에서 왼쪽 서브트리의 최댓값을 찾는 방법, 오른쪽 서브트리의 최솟값을 찾는 방법이 있습니다. 그래서 AVL 트리라고 모두 같은 모양이 나오지 않습니다. 아무튼, 제 코드를 실행하면 아래와 같은 결과를 얻을 수 있습니다.
public class Main {
public static void main(String[] args) {
// 현재 코드 : 이진탐색트리 예시
AVL tree = new AVL();
tree.insert(10);
tree.insert(20);
tree.insert(30);
tree.insert(40);
tree.insert(50);
tree.insert(25);
tree.delete(10);
tree.insert(9);
tree.delete(10);
tree.insert(45);
tree.insert(55);
tree.insert(49);
tree.delete(45);
tree.traverse();
}
}
// return value는 아래와 같습니다.
// left node -> 20 // right node -> 49
// left node -> 9 // right node -> 25
// left node -> null // right node -> null
// left node -> null // right node -> null
// left node -> 40 // right node -> 50
// left node -> null // right node -> null
// left node -> null // right node -> 55
// left node -> null // right node -> null
전체 코드
전체 코드는 다음과 같습니다.
// AVL.java
package tree;
public class AVL implements Tree {
private Node root;
int height(Node node) {
if (node == null)
return -1;
return node.height;
}
@Override
public void insert(Integer data) {
this.root = insert(this.root, data);
}
@Override
public void delete(Integer data) {
Node node = delete(this.root, data);
if (node == null) {
// 트리에 데이터가 없는 경우
return;
}
}
@Override
public void traverse() {
if (this.root != null) {
traverse(this.root);
} else {
System.out.println("해당 트리는 비어있습니다.");
}
}
private void traverse(Node node) {
// preorder
if (node != null) {
System.out.print(node.data);
if (node.left != null) {
System.out.print(" // left node -> "+node.left.data);
} else {
System.out.print(" // left node -> null");
}
if (node.right != null) {
System.out.print(" // right node -> "+node.right.data);
} else {
System.out.print(" // right node -> null");
}
System.out.println();
traverse(node.left);
traverse(node.right);
}
}
private Node delete(Node node, Integer data) {
if (node == null) {
return null;
}
// 삭제할 값을 찾는 중
if (data < node.data) {
node.left = delete(node.left, data);
} else if (data > node.data) {
node.right = delete(node.right, data);
}
else {
// 삭제할 값 발견 -> 대체할 노드를 찾아야 한다.
// 자식의 개수에 따라서 삭제된 노드를 대체하는 노드가 달라진다 (자식 입장에서 부모를 찾을 수 없음 -> 그래서 값을 바꾸는 방식을 사용)
if (node.getChildCnt() == 0) {
node = null;
} else {
if (node.left != null) { // 좌측 subtree에서 가장 큰 값을 찾는다(left에 자식이 있음)
Node target = findMaxNode(node.left);
node.data = target.data;
node.left = delete(node.left, target.data);
} else { // 자식이 1개(right에만) -> 자식을 자신의 위치로 올리면 된다
node = node.right;
}
}
}
if (node == null) { // Leaf노드가 삭제된 케이스
return null;
}
// 높이를 다시 정의한다
// node에서 밸런스가 깨지지 않았는지 검사한다
node.height = Math.max(height(node.left),height(node.right)) + 1;
int balance = getBalance(node);
// left-left
if (balance > 1 && data < node.left.data) {
return rightRotate(node);
}
// right-right
if (balance < -1 && data > node.right.data) {
return leftRotate(node);
}
// left-right
if (balance > 1 && node.left.data < data) {
node.left = leftRotate(node.left); // 왼쪽 자식노드에 대해 먼저 좌회전을 한다
return rightRotate(node);
}
// right-left
if (balance < -1 && data < node.right.data) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 변경사항이 없을 경우
return node;
// 밸런스가 깨지지 않았는가 검사한다
}
private Node findMaxNode(Node node) {
// max Value를 찾고,
if (node.right != null) {
return findMaxNode(node.right);
} else {
return node;
}
}
private Node insert(Node node, Integer data) {
// BST 삽입을 수행
// 트리의 첫 값이 삽입되었을 때 새로운 노드를 만든다 -> 해당 노드는 root가 된다
if (node == null) {
return new Node(data);
}
if (data < node.data) {
node.left = insert(node.left, data);
} else if (data > node.data) {
node.right = insert(node.right, data);
} else { // 이미 트리에 존재하는 값을 삽입하려 할 때 -> root를 반환한다
return node;
}
// 삽입 후 검사(삽입 결과가 left-left인지, right-right인지....)
node.height = 1 + Math.max(height(node.left), height(node.right));
int balance = getBalance(node);
// left-left
if (balance > 1 && data < node.left.data)
return rightRotate(node);
// right-right
if (balance < -1 && data > node.right.data) {
return leftRotate(node);
}
// left-right
if (balance > 1 && node.left.data < data) {
node.left = leftRotate(node.left); // 왼쪽 자식노드에 대해 먼저 좌회전을 한다
return rightRotate(node);
}
// right-left
if (balance < -1 && data < node.right.data) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 변경사항이 없을 경우
return node;
}
private Node rightRotate(Node parent) {
if (parent.left == null) {
return parent;
}
Node newParent = parent.left;
Node T2 = newParent.right; // 적절한 이름? 회전 기준노드의 우측 sub 노드
// 회전
newParent.right = parent;
parent.left = T2;
// update Height ( 현재 트리 기준 자식(원래 부모) 먼저 갱신 -> 그래야 부모가 제대로 갱신)
parent.height = Math.max(height(parent.left), height(parent.right)) + 1;
newParent.height = Math.max(height(newParent.left), height(newParent.right)) + 1;
return newParent;
}
private Node leftRotate(Node parent) {
if (parent.right == null) {
return parent;
}
Node newParent = parent.right;
Node T2 = newParent.left;
newParent.left = parent;
parent.right = T2;
parent.height = Math.max(height(parent.left), height(parent.right)) + 1;
newParent.height = Math.max(height(newParent.left), height(newParent.right)) + 1;
return newParent;
}
private int getBalance(Node node) {
if (node == null) {
return 0;
}
return height(node.left) - height(node.right);
}
static class Node {
Integer data; // 제너릭스
Node left;
Node right;
int height;
public Node(Integer data) {
this.data = data;
height = 0;
}
public int getChildCnt() {
int temp = 0;
if (left != null) {
temp += 1;
}
if (right != null) {
temp += 1;
}
return temp;
}
}
}
끝마치며
AVL 트리를 통해 이진탐색트리의 약점을 보완할 수 있게 되었습니다. 하지만, AVL 트리는 좀 엄격한 자료구조입니다. 삽입/삭제가 일어났을 때 회전이 빈번하게 발생합니다. 다시 말해, 자료구조를 정렬하는 데 시간이 어느 정도 소요됩니다. 이 부분을 보완하기 위해 Red-Black 트리라는 자료구조가 만들어지는데요.
실제로 AVL 트리보다 Red-Black 트리가 더 자주 사용됩니다. (AVL 트리 역시 여전히 사용됩니다)
여기까지 공부를 끝마치신 여러분은 다음으로 Red-Black 트리를 공부하는 걸 권해드립니다.
저 역시 이후에 Red-Black Tree에 대해 글을 작성할텐데, 해당 글에 AVL 트리와 Red-Black 트리의 장단점, 어떤 상황에서 어떤 자료구조가 더 유용한지에 대해 함께 작성하도록 하겠습니다. 읽어주셔서 감사합니다.
출처:
