AVL Tree를 알아보자

soonbee·2020년 5월 17일

일반적인 이진검색트리에서는 트리구조가 한 쪽으로 치우쳐지는 경우가 발생할 수 있습니다. 이진검색트리의 평균 검색속도는 O(logN)이지만 한 쪽으로 치우쳐진 경우에는 검색속도가 O(N)까지 저하될 수 있죠. 이를 방지하기 위해 리밸런싱 작업을 수행하는 자료구조로는 AVL Tree, B-Tree, Red-Black Tree 등이 있으며 그 중 AVL Tree에 대해 알아보려고 합니다.

우선 AVL Tree가 어떻게 리밸런싱을 하는지 예시를 봅시다. 아래 그림과 같이 트리가 있습니다.

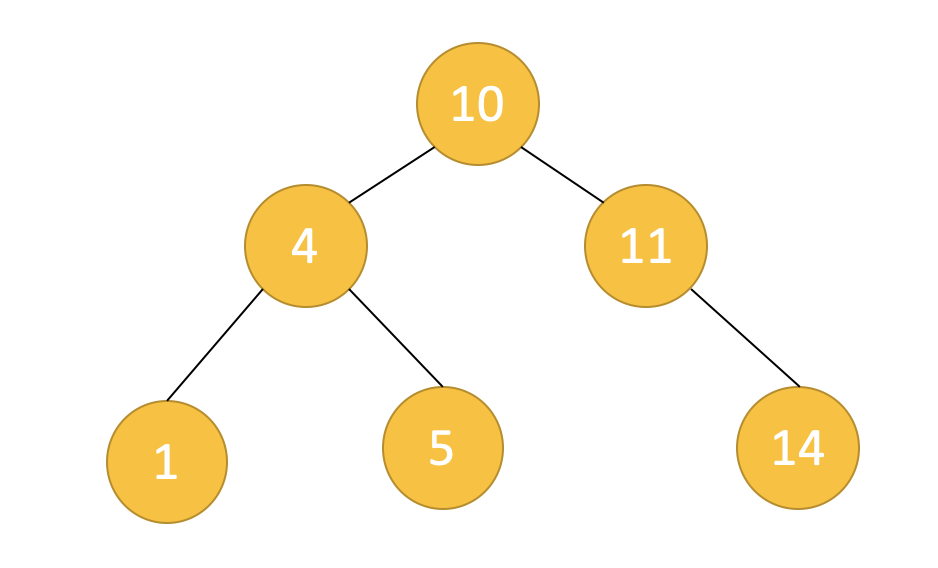
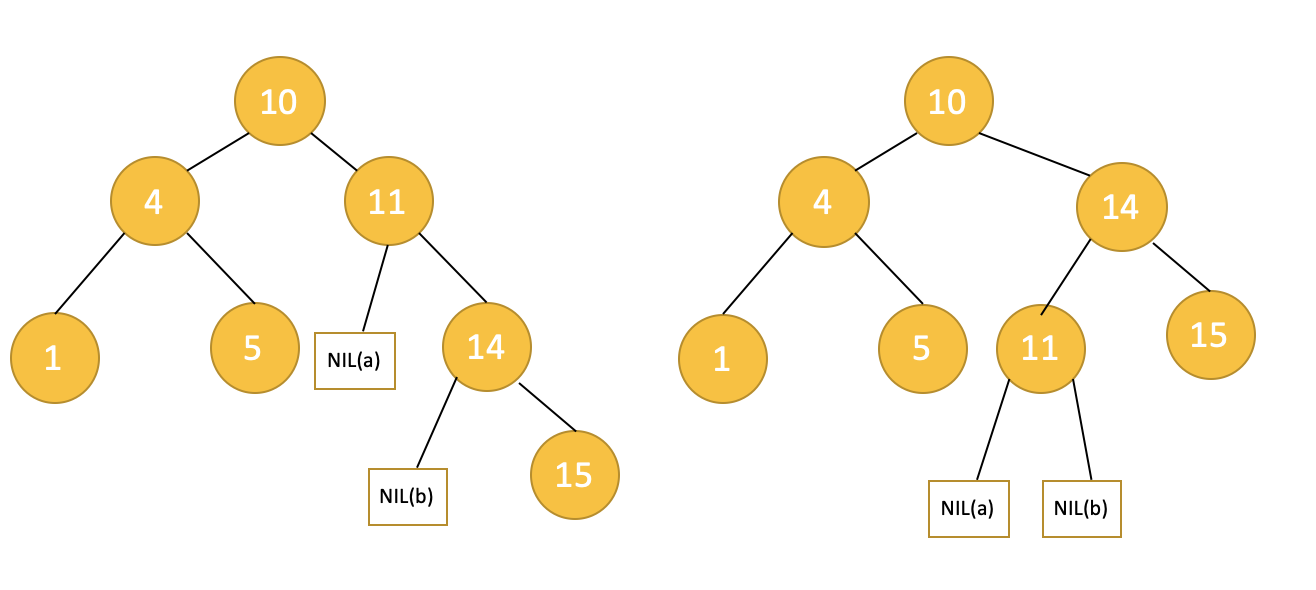
여기에 15를 삽입하겠습니다. 이진검색트리이므로 다음과 같이 될 거라고 예상할 수 있습니다.

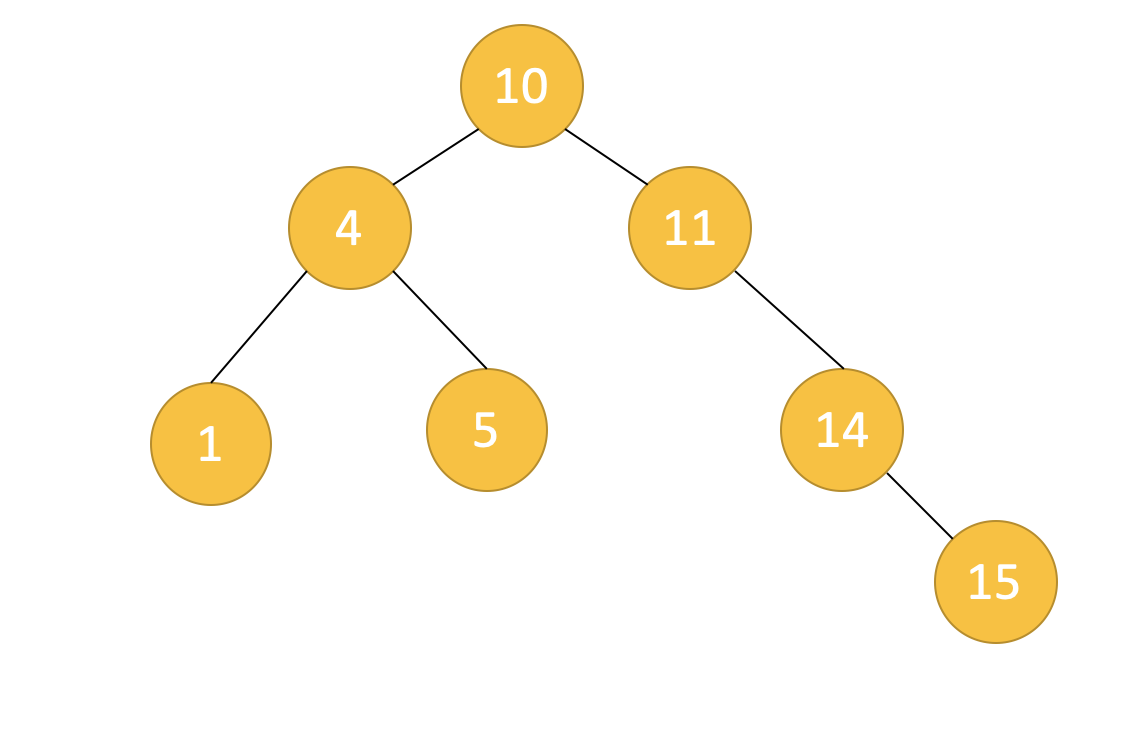
AVL Tree의 경우 데이터가 삽입되고나서 불균형이 발견되면 리밸런싱 작업을 수행하며 그 결과는 아래와 같습니다.

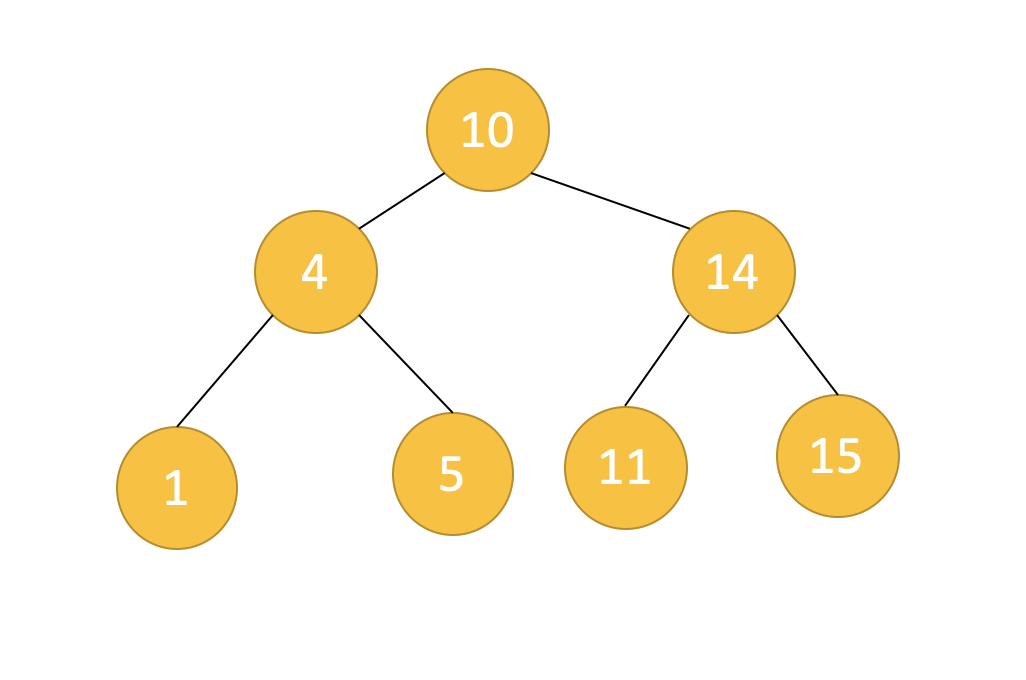
무언가 이전 상태보다 균형이 잡혔다는 느낌이 늘지 않나요? 그럼 이제 AVL Tree에 대해 자세하게 알아봅시다. AVL Tree에 대해 이해하기 위해서는 불균형의 기준이 무엇인가와 균형을 맞추기 위한 트리의 재구성을 어떻게 하는가에 대해 알 필요가 있습니다.

불균형 상태

AVL Tree에서 불균형이 발생하면 리밸런싱을 합니다. 그럼 어떤 상태를 불균형한 상태라고 볼 수 있을까요? AVL Tree에서는 하나의 노드를 기준으로 양쪽 서브트리의 높이 차이가 2 이상인 경우를 의미합니다. 처음에 보았던 예시를 다시 한 번 보죠. 각 노드들의 높이를 적어두었습니다. 자식노드가 없는 리프노드(leaf node)의 경우는 높이가 1이며 리프노드로부터 부모노드로 한단계씩 올라갈때마다 높이를 1씩 증가시키면 됩니다. 서브트리가 비어있는 경우에 높이는 0 입니다.

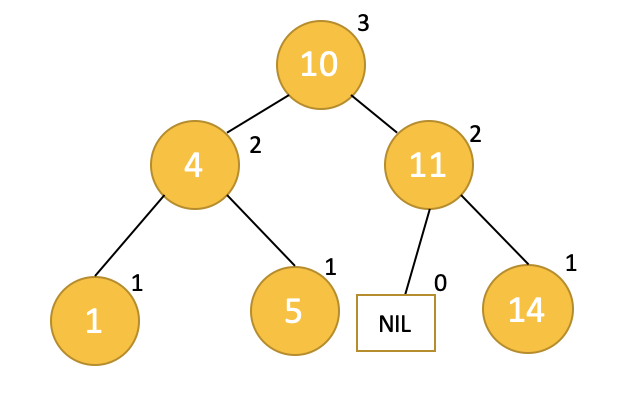
트리에 15를 삽입하였고 그 결과 삽입된 데이터의 상위 노드들은 모두 높이가 1씩 증가합니다.

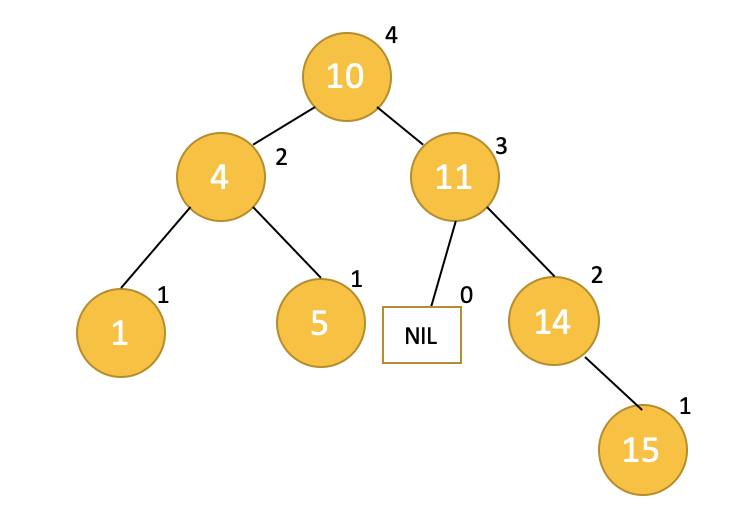
노드 11을 봅시다. 11의 왼쪽자식이 존재하지 않으므로 왼쪽서브트리의 높이는 0이고 오른쪽 서브트리의 높이는 2입니다. 아까 불균형의 조건은 좌우 서브트리의 높이차가 2 이상인 경우라고 했죠? 따라서 불균형이 발생했다고 할 수 있습니다. AVL Tree에서는 균형을 맞추기 위해 리밸런싱 작업을 수행합니다. 어떻게 리밸런싱을 할까요? 바로 회전이라는 작업을 통해 이루어집니다.

트리의 회전

정확히는 트리를 재구조화하는 작업입니다. 재구조화된 결과가 마치 트리가 회전한 것처럼 되어서 회전이라고 부르죠. 회전의 종류로는 left rotation 과 right rotation 이 있습니다.

left rotation

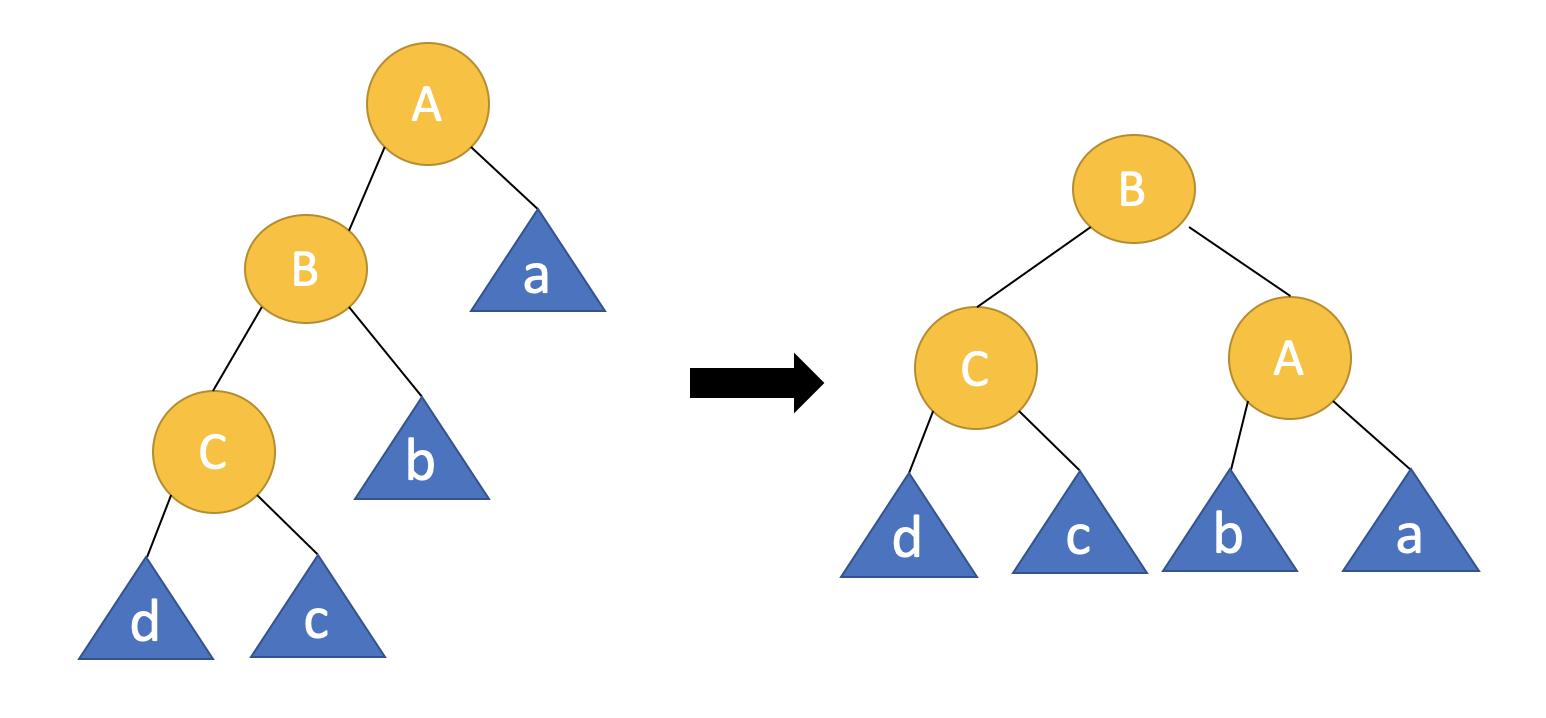
먼저 left rotation을 알아봅시다. a, b, c는 서브트리를 의미합니다. 서브트리는 노드가 단 1개일수도 혹은 비어있을 수도 있습니다. 회전 기준은 노드 A입니다.

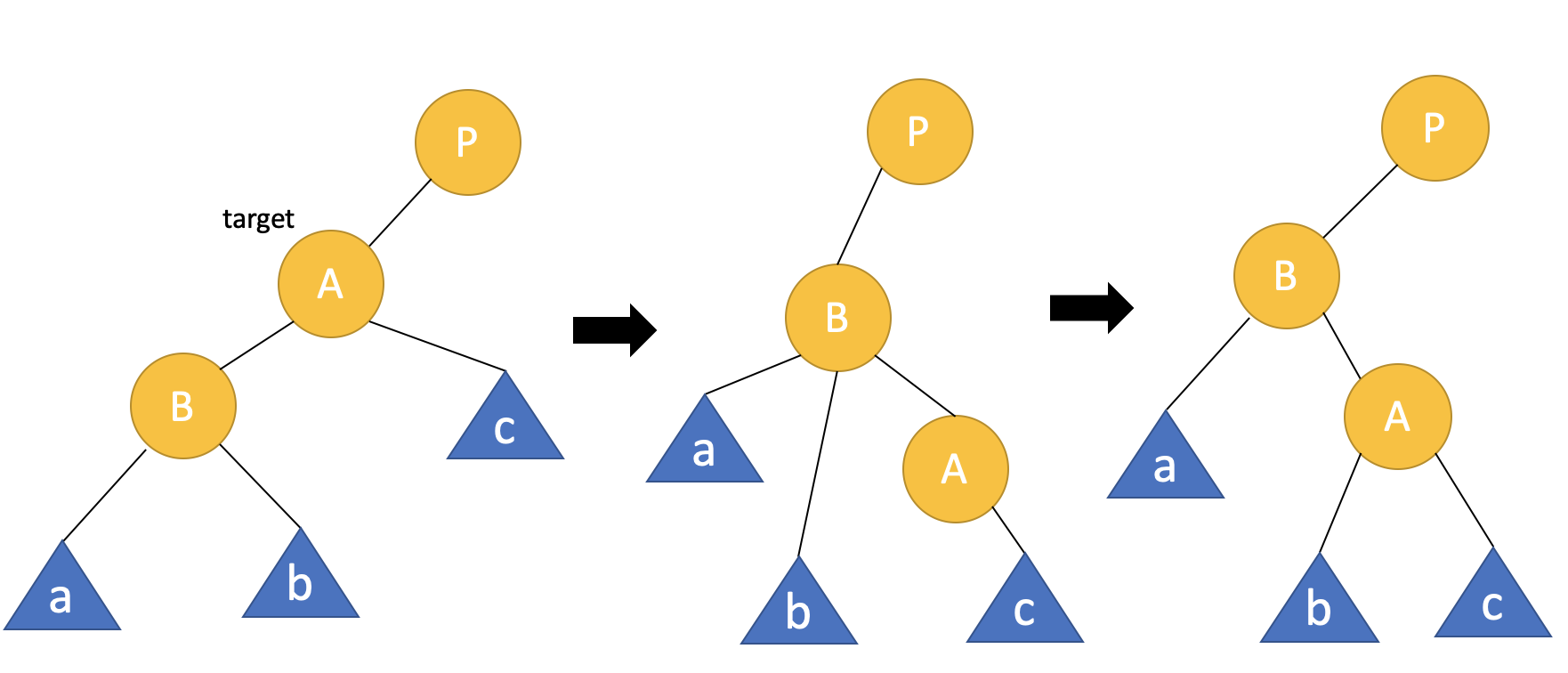
어려워 보이지만 생각보다 복잡한 로직은 아니에요. 너무 어렵게 생각하지 않아도 됩니다. 회전하면서 노드 A의 위치를 노드 B가 대신하고, 그 과정에서 노드 B의 자식이 3개가 되므로 서브트리 b의 위치를 조정합니다. 서브트리 b의 위치조정은 'b는 A보다 작고 B보다 크다' 가 'b는 B보다 크고 A보다 작다' 로 말의 순서가 바뀐 거라고 생각하면 됩니다.

left rotation의 수도코드를 아래와 같이 표현할 수 있습니다.

target.parent.right = target.right
tmp = target.right.left
target.right.left = target
target.right = tmp

right rotation

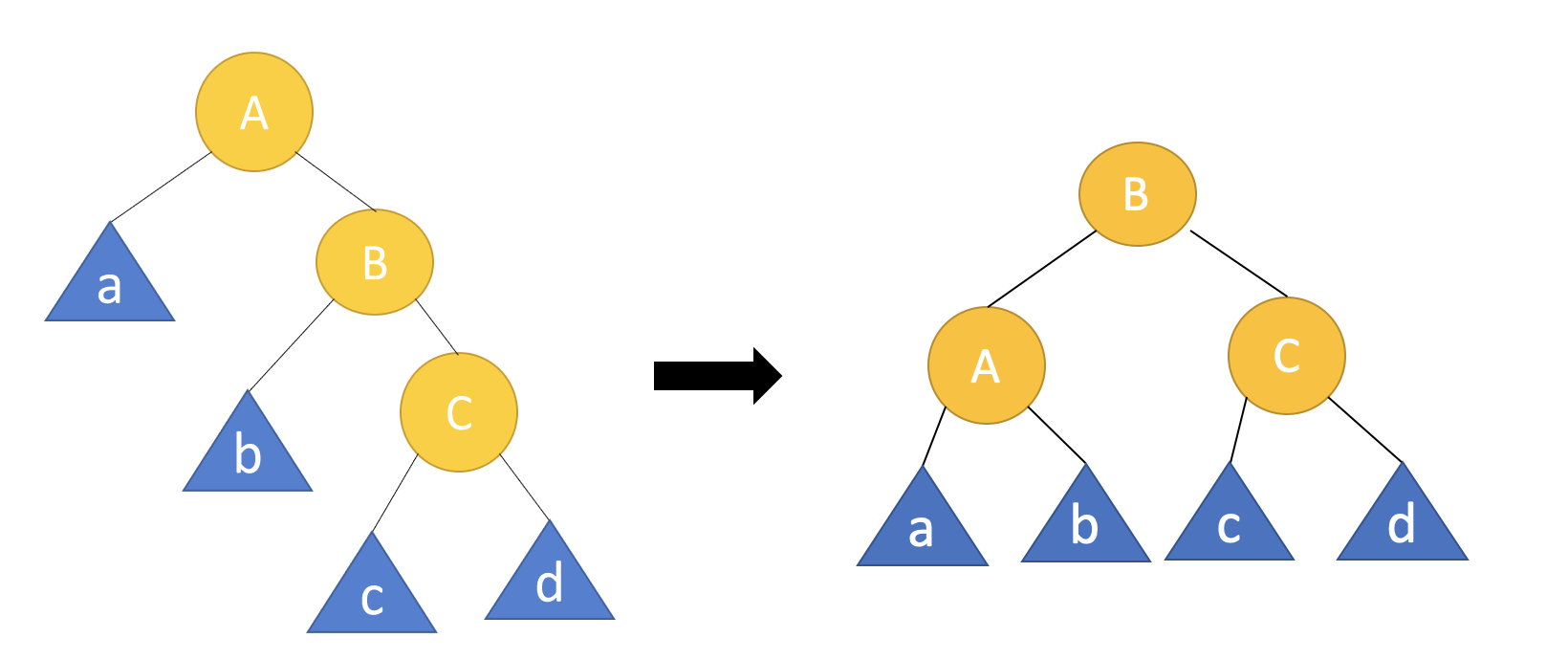
다음은 right rotation입니다. 마찬가지로 a, b, c는 서브트리이고 회전기준은 노드 A입니다.

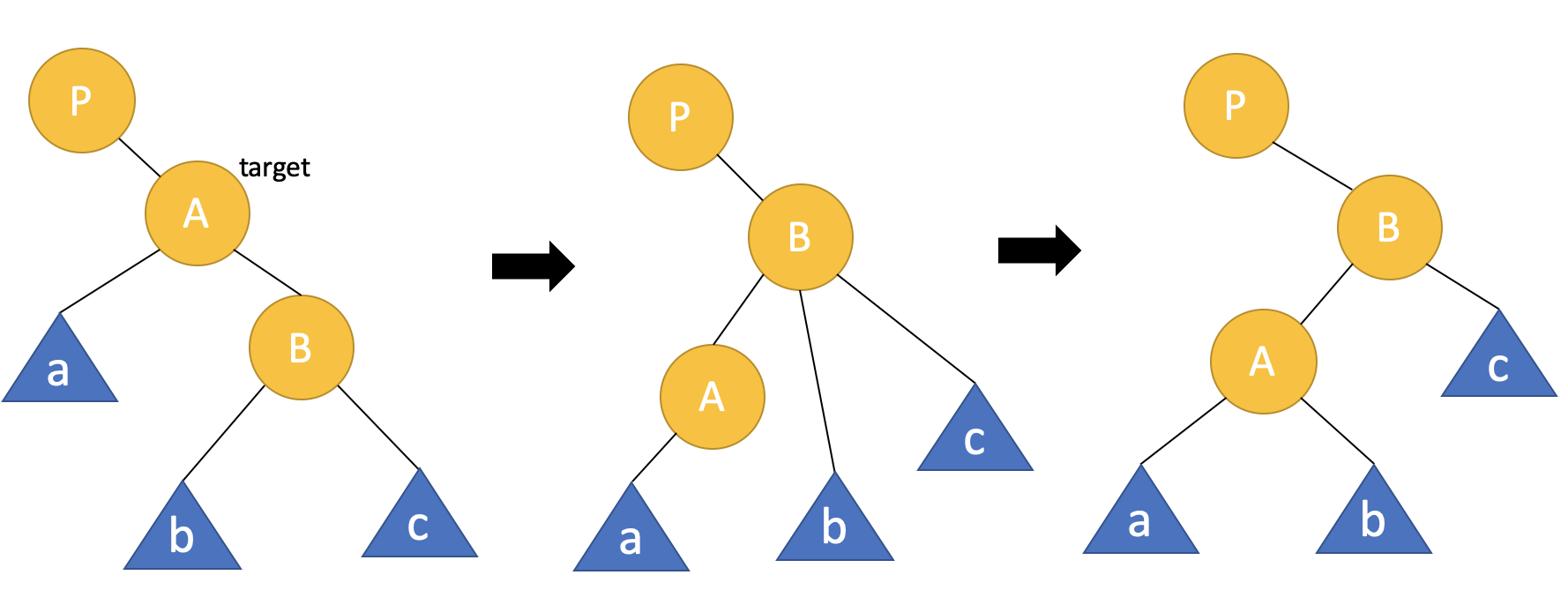
right rotation도 마찬가지로 회전하면서 노드 A의 위치를 노드 B가 대신하고 서브트리 b의 위치를 조정합니다. 'b는 A보다 크고 B보다 작다' 가 'b는 B보다 작고 A보다 크다'로 말의 순서만 바뀌었다는 걸 기억하세요.

right rotation의 수도코드는 아래와 같습니다.

target.parent.left = target.left
tmp = target.left.right
target.left.right = target
target.left = tmp

rotation 예제

그럼 회전을 사용해봅시다. 위에서 사용했던 예시를 가져오겠습니다.

15가 삽입되었고 그 결과 노드 11을 기준으로 불균형이 발생한 상태입니다. 그럼 노드 11을 기준으로 left rotation을 적용하겠습니다. 왜 left rotaion을 적용해야 하는지에 대해서는 아래에서 설명하겠습니다.

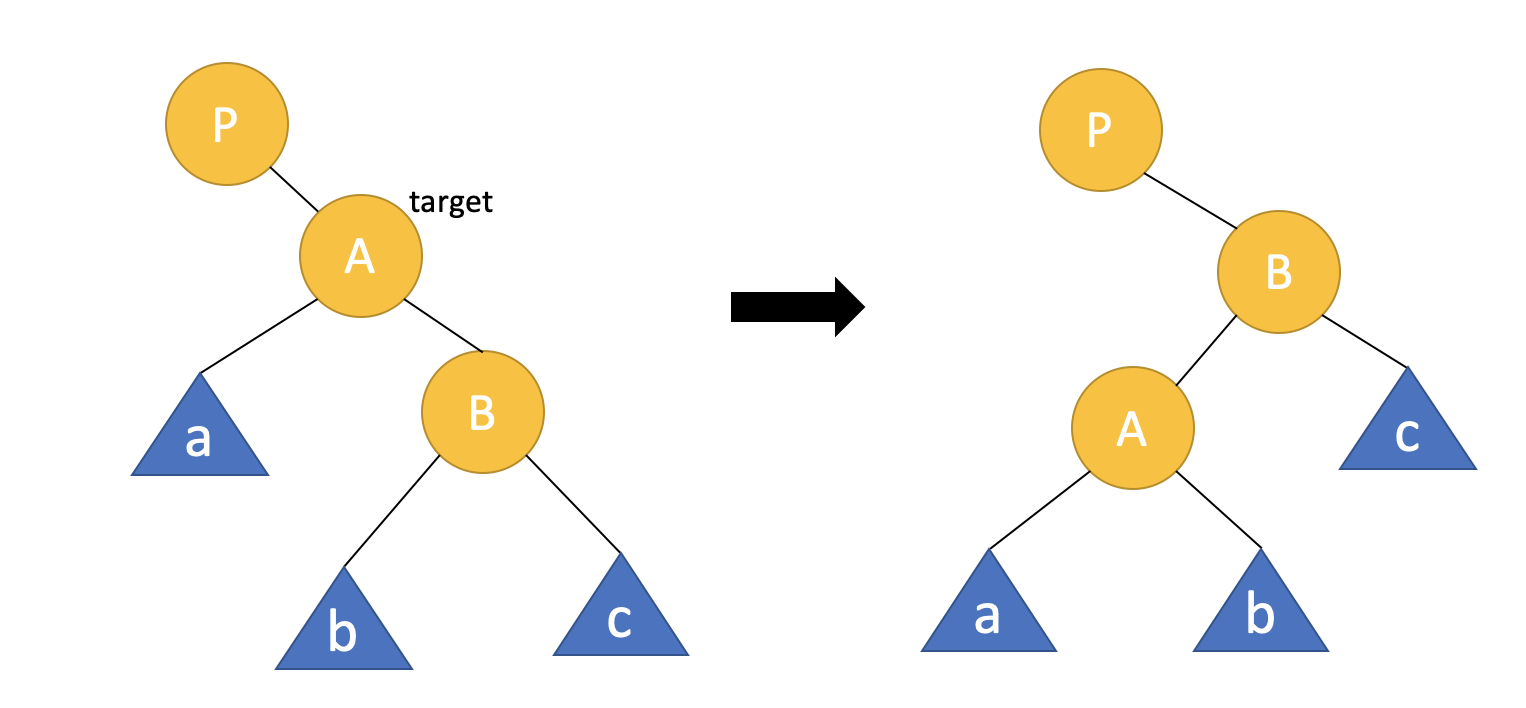
하나씩 매칭해보면 P = 노드 10, A = 노드 11, B = 노드 14입니다. NIL은 각각 NIL(a), NIL(b) 로 구분하였습니다. 회전 결과 트리의 불균형이 사라졌습니다.

rotation case

불균형 상태인지 아닌지 판단도 할 수 있고 해결하기 위한 방법도 배웠습니다. 그럼 left rotation과 right rotation을 언제 적용해야 하는지 알아봅시다. 총 4가지의 경우가 있습니다. 불균형이 발생한 노드는 A입니다.

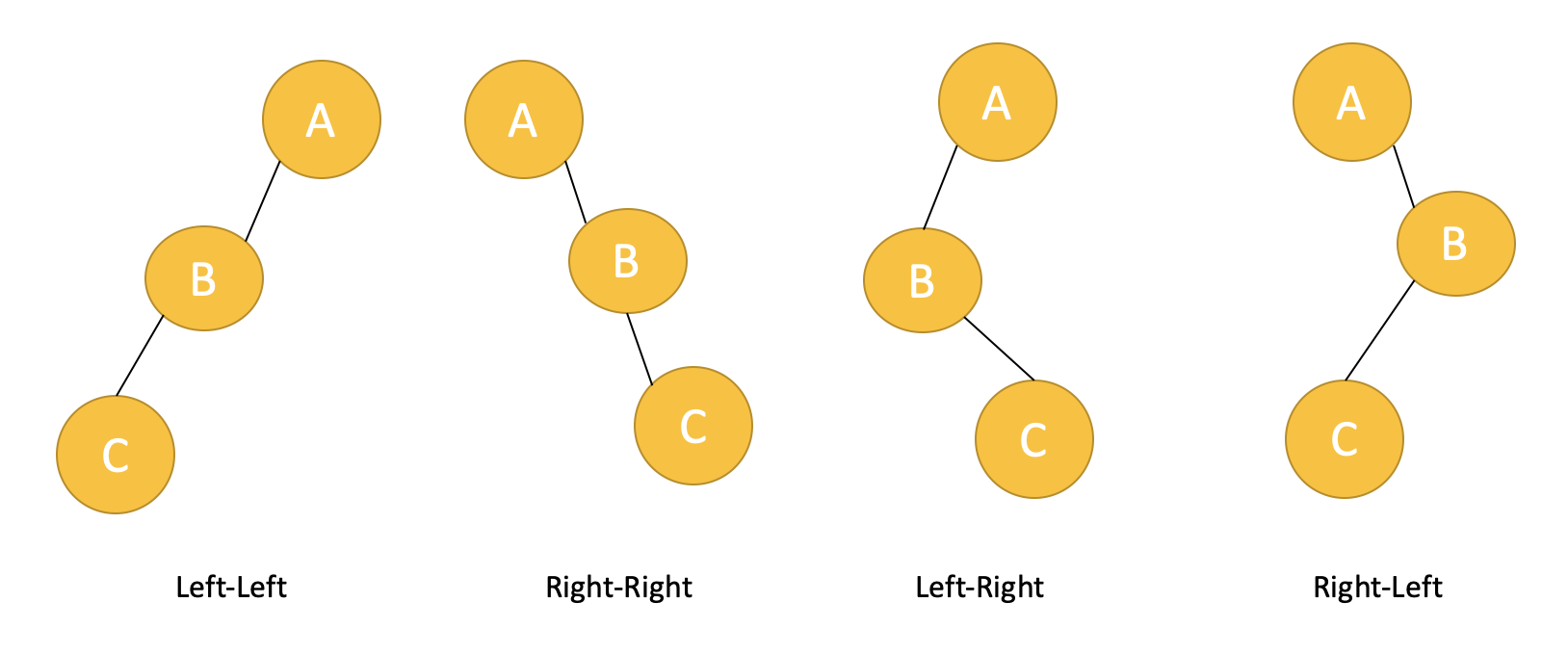
Left-Left (LL)

Left-Left 인 경우에는 A노드를 기준으로 right rotation을 진행합니다.

Right-Right (RR)

Right-Right 인 경우에는 A노드를 기준으로 left rotation을 진행합니다.

Left-Right(LR)

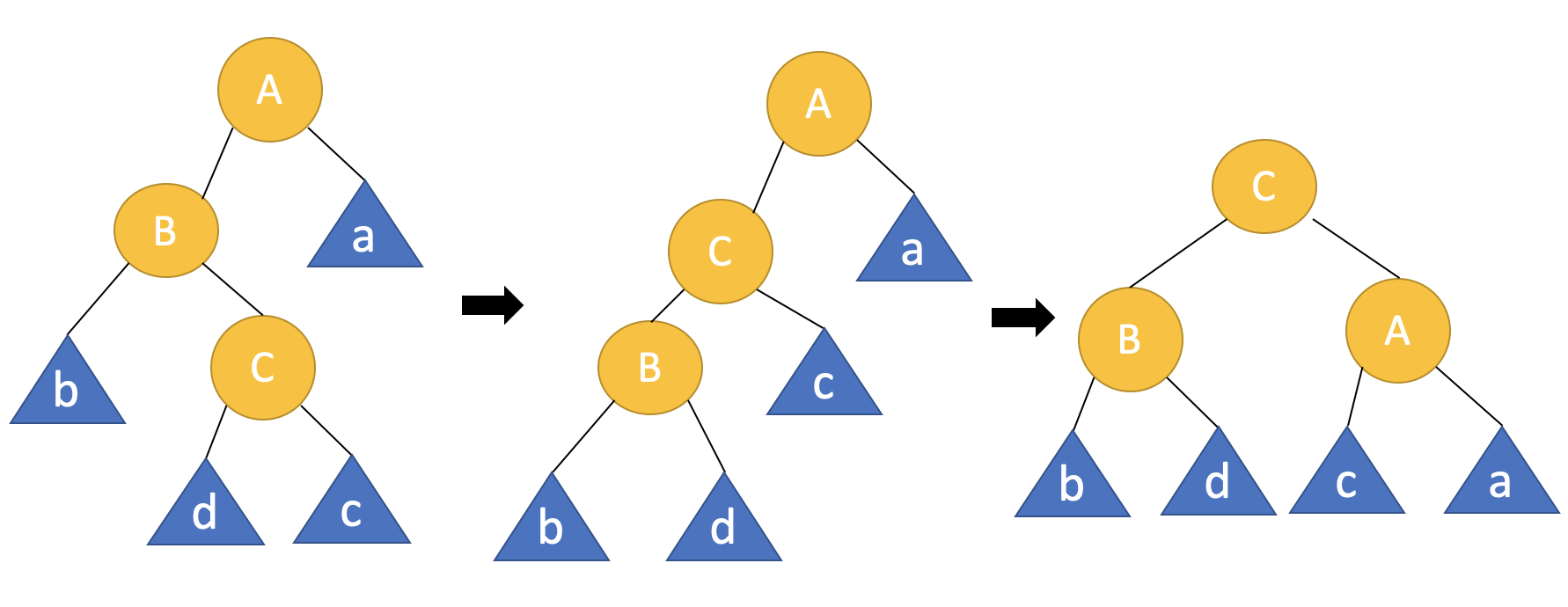
Left-Right인 경우에는 두 단계를 거쳐야 합니다.

우선 노드 B를 기준으로 left rotation을 진행한 후 노드 A를 기준으로 right rotation을 진행합니다.

Right-Left(RL)

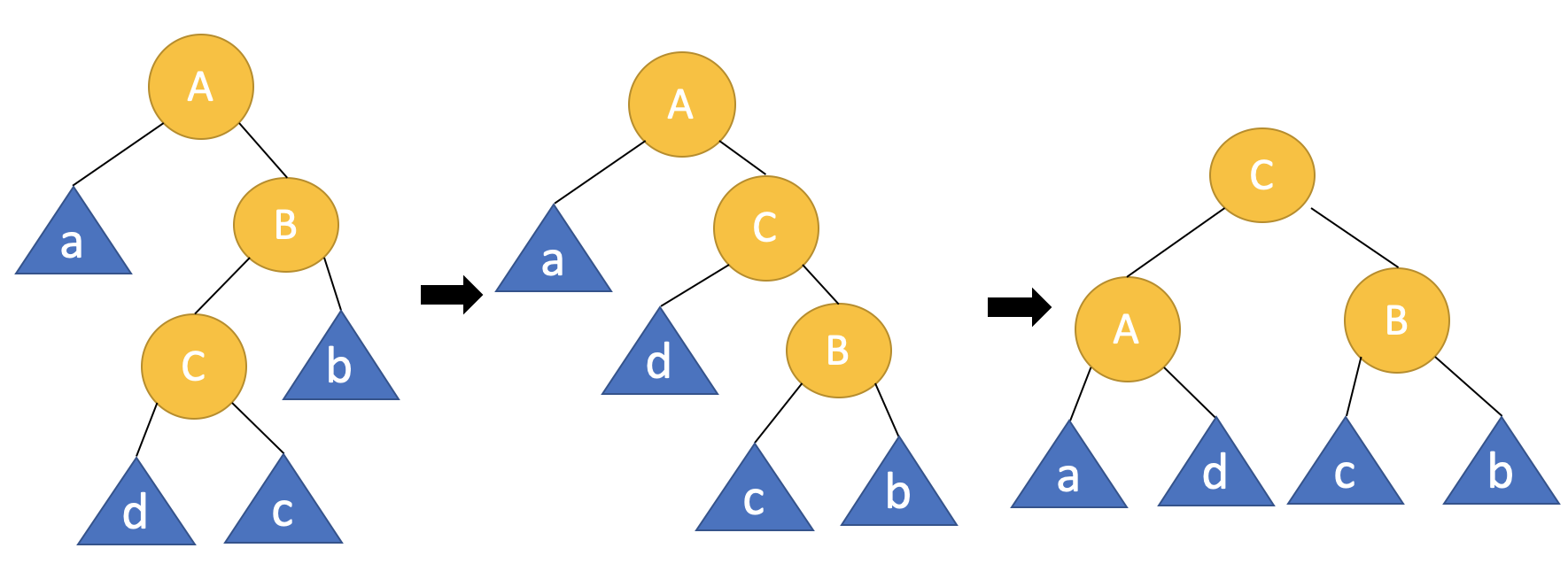
Left-Right인 경우에는 두 단계를 거쳐야 합니다..

우선 노드 B를 기준으로 right rotation을 진행한 후 노드 A를 기준으로 left rotation을 진행합니다.

서브트리의 결정

여기서 한 가지 헷갈리는 게 과연 '누가 서브트리이고 누가 회전의 축이 되는 노드인가?' 입니다.

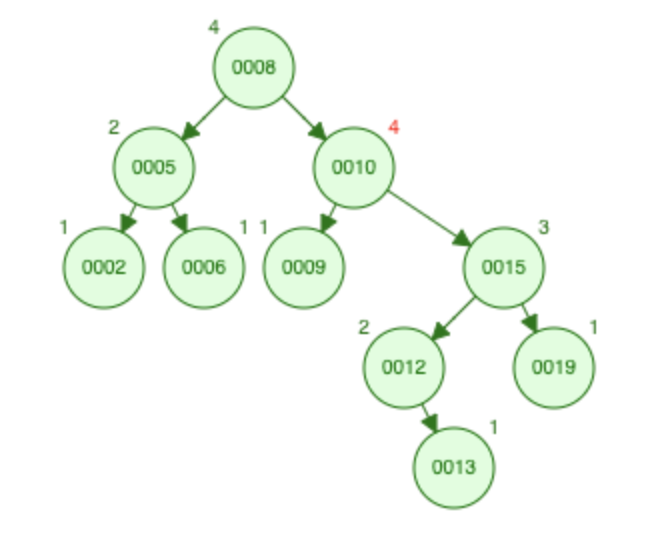
위 그림에서는 노드 10에서 불균형이 발생했습니다. 그럼 노드 A = 노드 10, 노드 B = 노드 15 까지는 쉽게 구분이 되죠. 그럼 노드 12 와 노드 19 중 누가 노드 C이고 누가 서브트리 b일까요? 정답은 높이가 낮은 쪽이 서브트리입니다. 위 그림에서는 노드 12 = 노드 C이고 노드 19 = 서브트리 b 이므로 RL case 입니다.

heightDiff = node.left.height - node.right.height

LL: target.heightDiff > 1 && target.left.heightDiff >= 0

RR: target.heightDiff < -1 && target.right.heightDiff <= 0

LR: target.heightDiff > 1 && heightDiff > 1 && target.left.heightDiff < 0

RL: target.heightDiff < -1 && target.right.heightDiff > 0

만약 높이가 같다면 어떨까요? 그런 경우에는 어느 쪽을 서브트리라고 해도 상관없습니다. 그러나 굳이 쉬운 길을 어렵게 돌아갈 필요는 없죠. 높이가 같아 RR case, RL case 둘 다 된다면 RR case로 생각하고 LL case, LR case 둘 다 가능한 상황이라면 LL case라고 생각하면 됩니다.

삽입연산

이진트리라고 생각하고 데이터를 삽입하면 됩니다. 삽입할 데이터가 기준 노드보다 작다면 왼쪽, 크다면 오른쪽으로 이동합니다. 반복하다가 비어있는 자리를 발견하면 위치시킵니다. 새로운 데이터가 삽입됨에 따라 트리가 불균형해졌을수도 있습니다. 이를 검사하기 위해 삽입된 위치로부터 루트노드까지 올라가면서 불균형 여부를 검사합니다. 불균형이 발견되면 case에 따라 회전연산을 적용하면 됩니다.

삭제연산

삽입과 마찬가지로 삭제 후 루트노드로 이동하면서 불균형이 발견되면 case에 따라 회전연산을 적용합니다. 삭제하는 방법은 3가지 경우 나눌 수 있습니다.

리프노드

삭제할 노드가 리프노드인 경우에는 쉽게 삭제하기만 하면 됩니다.

자식노드가 하나인 경우

자식노드가 있는데 한쪽에만 있는 경우 노드를 삭제하고 삭제한 노드의 위치를 자식노드가 대신하면 됩니다.

자식노드가 둘 다 있는 경우

자식노드가 둘 다 있는 경우에는 삭제하기 전 데이터 교환이 필요합니다. 삭제할 노드를 기준으로 좌측 서브트리의 최대값 노드 혹은 우측 서브트리의 최소값 노드를 찾은 후 데이터를 교환합니다. 보통 좌측 서브트리의 최대값 노드를 사용합니다. 데이터를 교체하면 좌측 서브트리의 최대값 노드 위치에 삭제할 데이터가 있게 되고 이 상태에서 노드를 삭제하면 됩니다.