[TIL] 자료구조/알고리즘 풀기 (3)

학습 주제

---

1. 큐(Queue)

2. 환형 큐(Circular Queue)

3. 우선순위 큐(Priority Queue)

4. 트리(Tree)

5. 이진 트리(Binary Tree)

6. 이진 트리 - 넓이 우선 순회(Breadth First Traversal)

7. 이진 탐색 트리(Binary Search Tree)

8. 힙(Heap)
   
   

1. 큐(Queue)

---

• 선입선출(FIFO)의 특징을 갖는 선형 자료구조

• 자료를 생성하는 작업과 그 자료를 이용하는 작업이 비동기적으로 일어나는 경우 활용
  
  

• 추상자료형
  - size(): 현재 큐의 데이터 원소 수 계산

  - isEmpty(): 현재 큐가 비어있는지를 판단
  - enqueue(x): 데이터 원소 x를 큐에 추가
  - dequeue(): 큐의 최전방 데이터 원소를 추출
  - peek(): 큐의 최전방 데이터 원소를 반환

  
  

• 구현

  1. 배열로 구현

       class ArrayQueue:
     		def __init__(self):
     			self.data = []
     
     		def size(self):
     			return len(self.data)
     
     		def isEmpty(self):
     			return self.size() == 0
     
     		def enqueue(self, item):
     			self.data.append(item)
     
     		def dequeue(self):
     			return self.data.pop(0)
     
     		def peek(self):
     			return self.data[0]

     • dequeue() 연산의 시간복잡도가 O(N)
       
       

  2. 양방향 연결 리스트로 구현

       class LinkedListQueue:
     		def __init__(self):
       			self.data = DoublyLinkedList()
     
     	    def size(self):
       			return self.data.getLength()
     
     		def isEmpty(self):
       			return self.size() == 0
     
     	    def enqueue(self, item):
       			node = Node(item)
       			self.data.insertAt(self.size() + 1, node)
     
     		def dequeue(self):
       			return self.data.popAt(1)
     
     	    def peek(self):
       			return self.data.getAt(1).data

2. 환형 큐(Circular Queue)

---

• 정해진 개수의 저장 공간을 돌면서 이용하는 큐
  
  

• 추상자료형

  • size(): 현재 큐의 데이터 원소 수 계산

  • isEmpty(): 현재 큐가 비어있는지를 판단

  • isFull(): 현재 큐가 가득 차있는지를 판단

  • enqueue(x): 데이터 원소 x를 큐에 추가

  • dequeue(): 큐의 최전방 데이터 원소를 추출

  • peek(): 큐의 최전방 데이터 원소를 반환
    
    

• 구현

  class CircularQueue:
        def __init__(self, n):
        	self.maxCount = n
            self.data = [None] * n
            self.count = 0
            self.front = -1
            self.rear = -1
  
        def size(self):
            return self.count
  
        def isEmpty(self):
            return self.count == 0
  
        def isFull(self):
            return self.count == self.maxCount
  
        def enqueue(self, x):
            if self.isFull():
                raise IndexError('Queue is full')
  
            self.rear = 0 if self.rear == self.maxCount - 1 else self.rear + 1
            self.data[self.rear] = x
            self.count += 1
  
        def dequeue(self):
            if self.isEmpty():
                raise IndexError('Queue is empty')
  
            self.front = 0 if self.front == self.maxCount - 1 else self.front + 1
            x = self.data[self.front]
            self.count -= 1
            return x
  
        def peek(self):
            if self.isEmpty():
                raise IndexError('Queue is empty')
  
            return self.data[0 if self.front == self.maxCount + 1 else self.front + 1]

3. 우선순위 큐(Priority Queue)

---

• FIFO 방식을 따르지 않고 원소들의 우선순위에 따라 큐에서 빠져나오는 큐

• 운영체제의 CPU 스케줄링에 활용
  
  

• 구현

  • enqueue()할 때 우선순위 순서를 유지하도록 하는 것이 조금 더 유리
    • dequeue()할 때 우선순위를 고려하면, 다른 모든 항목을 탐색해야 함
      
      
  • 양방향 연결 리스트로 구현하는 것이 배열로 구현하는 것보다 빠름
    
    

4. 트리(Tree)

---

• 노드와 간선(Edge)을 이용하여 데이터의 배치 형태를 추상화한 계층형 자료구조
  
  

• 구조

  

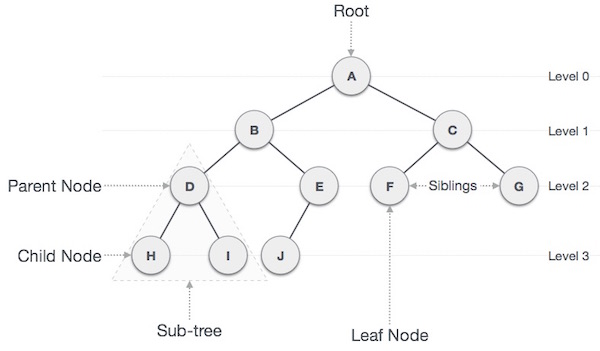
  • 루트 노드(Root): 트리의 최상위 노드
  • 단말 노드(Leaf): 자식이 없는 노드
  • 부모 노드(Parent)
  • 자식 노드(Child)
  • 형제 노드(Siblings) : 같은 부모를 갖는 노드
  • 서브 트리(Subtree) : 자신과 모든 자손으로 이루어진 트리
  • 간선(Edge) : 노드 간 연결선
  • 레벨(Level)
  • 깊이(Depth)
  • 차수(Degree): 자식(서브트리)의 수

5. 이진 트리(Binary Tree)

---

• 모든 노드의 차수가 2 이하인 트리

• 재귀적으로 정의 가능

  • 루트 노드 + 왼쪽 서브트리 + 오른쪽 서브트리
    
    

• 완전(Complete) 이진 트리

  • 마지막 레벨을 제외하고 모든 레벨이 노드로 완전히 채워져있는 트리

  • 마지막 레벨은 왼쪽부터 채워진 트리

  • 배열을 사용해 효율적으로 표현 가능

    

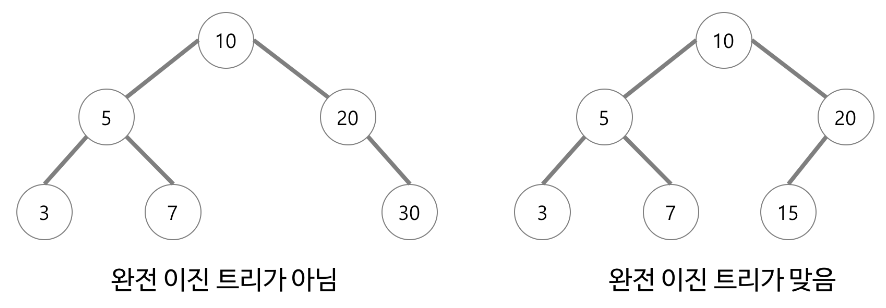
• 전(Full) 이진 트리

  • 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

    

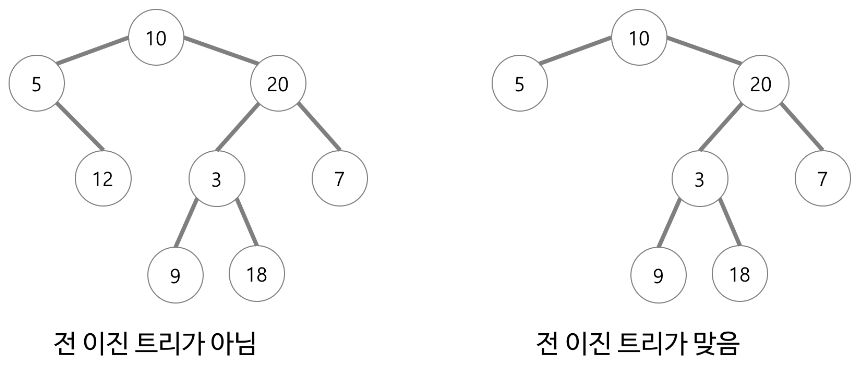
• 포화(Perfect) 이진 트리

  • 전 이진 트리이면서 완전 이진 트리인 경우

  • 말단을 제외한 모든 노드가 2개의 자식을 가짐

  • 모든 말단 노드가 동일한 레벨을 가짐

  • 노드의 개수가 항상 2^(k - 1)개
    - k: 트리의 높이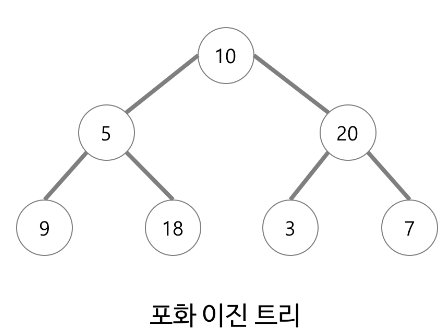

    

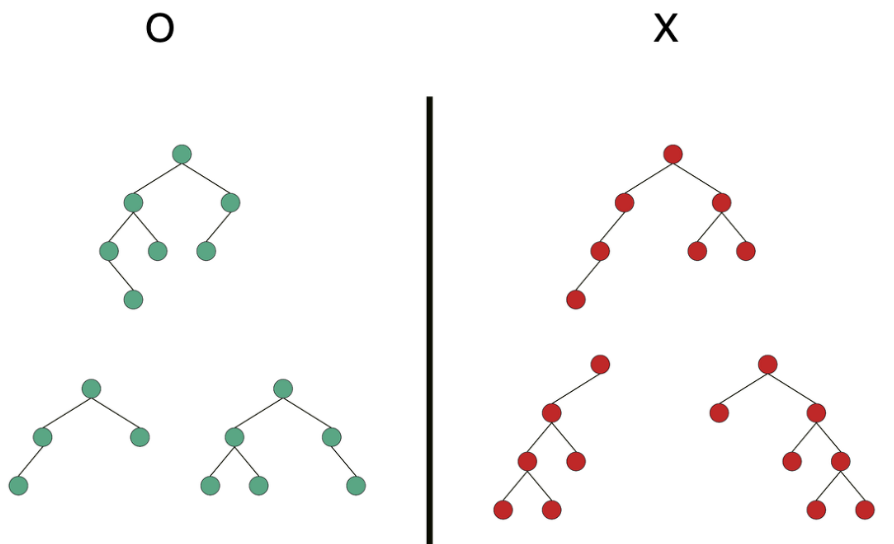
• 균형(Balanced) 이진 트리

  • 모든 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차가 1 이하인 트리

    

• 추상자료형

  • size(): 현재 트리에 포함되어 있는 노드의 수를 계산

  • depth(): 현재 트리의 깊이(= 높이)를 계산

  • 순회(Traversal)

    • 깊이 우선 순회(Depth First Traversal)
      • 중위 순회(In-order)
        • 왼쪽 자식 노드 → 현재 노드 → 오른쪽 자식 노드
      • 전위 순회(Pre-order)
        • 현재 노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드
      • 후위 순회(Post-order)
        • 왼쪽 자식 노드 → 오른쪽 자식 노드 → 현재 노드
          
          

  • 넓이 우선 순회(Breadth Fist Traversal)
    
    

• 구현

  class Node:
        def __init__(self, item):
            self.data = item
            self.left = None
            elf.right = None
  
        def size(self):
            l = self.left.size() if self.left else 0
            r = self.right.size() if self.right else 0
  
            return l + r + 1
  
        def depth(self):
            l = self.left.depth() if self.left else 0
            r = self.right.depth() if self.right else 0
  
            return max(l, r) + 1
  
        # preorder, postorder도 inorder와 거의 똑같고 순서만 다름
        def inorder(self):
            traversal = []
  
           if self.left:
               traversal += self.left.inorder()
  
           traversal.append(self.data)
  
           if self.right:
               traversal += self.right.inorder()
  
           return traversal

  class BinaryTree:
        def __init__(self, node):
            self.root = node
            
        def size(self):
            # 빈 트리가 아닌 경우
            if self.root:
                return self.root.size
                
            else:
                return 0
  
        def depth(self):
            if self.root:
                return self.root.depth()
        
            else:
                return 0
  
        def inorder(self):
            if self.root:
                return self.root.inorder()
                
            else:
                return []

6. 이진 트리 - 넓이 우선 순회(Breadth First Traversal)

---

• 레벨이 낮은 노드를 우선으로 방문

• 같은 레벨일 경우 부모 노드의 순서에 따라, 같은 부모일 경우 왼쪽부터 방문

  • 한 노드를 방문했을 때, 다음에 방문할 노드들을 큐에 순서대로 기록해야 함
    
    

• 재귀 적합 X
  
  

• 구현

  def bft(self):
      if not self.root:
          return []
  
      queue = ArrayQueue()
      queue.enqueue(self.root)
  
      traversal = []
  
      while not queue.isEmpty():
          popped = queue.dequeue()
          traversal.append(popped.data)
  
          if popped.left:
              queue.enqueue(popped.left)
  
          if popped.right:
              queue.enqueue(popped.right)
  
      return traversal

7. 이진 탐색 트리(Binary Search Tree)

---

• 모든 노드에 대해, 왼쪽 서브트리의 데이터는 모두 현재 노드의 값보다 작고, 오른쪽 서브트리의 데이터는 모두 현재 노드의 값보다 큰 이진 트리

• 이진 탐색에 비해 데이터 원소 추가, 삭제 용이

  • But, 공간 소요 큼
    
    

• 노드의 값이 연속적일 경우, 한쪽으로만 치우치기 때문에 효율적이지 못함
  -> AVL tree와 같이 높이의 균형을 유지하도록 구현하면, 탐색 효율성 보장 가능
  
  

• 추상자료형

  • insert(key, data): 트리에 주어진 데이터 원소 추가

  • remove(key): 트리에서 특정 원소 삭제

    • 자식의 개수에 따라 해야 할 연산이 다름

  • lookup(key): 트리에서 특정 원소 검색

  • inorder(): 키의 순서대로 데이터 원소 정렬

  • min(), max(): 최소 키, 최대 키를 갖는 원소 각각 탐색
    
    

• 구현

  class Node:
         def __init__(self, key, data):
             self.key = key
             self.data = data
             self.left = None
             self.right = None
  
          def inorder(self):
             traversal = []
  
             if self.left:
                 traversal += self.left.inorder()
  
             traversal.append(self)
  
             if self.right:
                 traversal += self.right.inorder()
  
             return traversal
  
          def min(self):
              if self.left:
                  return self.left.min()
  
              else:
                  return self
  
          def max(self):
              if self.right:
                  return self.right.max()
  
              else:
                  return self
  
          # parent의 default는 None
          # remove() 연산에서 parent 요구
          def lookup(self, key, parent = None):
              if key < self.key:
                  if self.left:
                      # 왼쪽 자식 노드의 부모는 현재 노드
                      return self.left.lookup(key, self)
  
                  else:
                      return None, None
  
              elif key > self.key:
                  if self.right:
                      return self.right.loopup(key, self)
  
                  else:
                      return None, None
  
              else:
                  return self, parent
  
          def insert(self, key, data):
              if key < self.key:
  
                  # 왼쪽 자식이 없는 경우, 삽입
                  if self.left is None:
                      self.left = Node(key, data)
  
                  # 있는 경우, 왼쪽 자식으로 insert() 메서드 재귀 호출
                  else:
                      self.left.insert(key, data)
  
              elif key > self.key:
                  if self.right is None:
                      self.right = Node(key, data)
  
                  else:
                      self.right.insert(key, data)
  
              # 인자로 받은 key값과 현재 노드의 key값이 같다면, KeyError 발생
              else:
                  raise KeyError
  
          def countChildren(self):
              count = 0
  
              if self.left:
                  count += 1
  
              if self.right:
                  count += 1
  
              return count

  class BinarySearchTree:
  		def __init__(self):
  		    self.root = None
  
  		def inorder(self):
  		    if self.root:
  			    return self.root.inorder()
  
  			else:
  				return []
  
  		def min(self):
  		    if self.root:
  			    return self.root.min()
  
  			else:
  				return None
  
  		def max(self):
  		    if self.root:
  			    return self.root.max()
  
  			else:
  				return None
  
  		def lookup(self, key):
  		    if self.root:
  			    return self.root.lookup(key)
  
  			else:
  				return None, None
  
  		def insert(self, key, data):
  		    if self.root:
  			    self.root.insert(key, data)
  
  			else:
  			    self.root = Node(key, data)

8. 힙(Heap)

---

• 완전 이진 트리의 한 종류

  • 노드의 추가/삭제는 마지막 노드에서만 수행

  • 배열로 구현하기 용이
    
    

• 루트 노드가 최댓값(Max Heap) or 최솟값(Min Heap)

• 재귀적으로 정의 가능

• 이진 탐색 트리와는 다르게 크기 순으로 정렬되어 있지 않기 때문에, 탐색이 빠르지 않음

• 삽입/삭제 연산의 시간복잡도는 O(log N)
  
  

• 추상자료형

  • init(): 빈 최대 힙 생성

  • insert(item): 새로운 원소 삽입

  • remove(): 최댓값 갖는 원소 추출
    
    

• 구현

  • 노드 번호가 m일 경우, 왼쪽 자식의 번호는 2m, 오른쪽 자식의 번호는 2m + 1

  • 부모 노드의 번호는 m // 2

  class MaxHeap:
      def __init__(self):
          self.data = [None]
  
      def insert(self, item):
          self.data.append(item)
          index = len(self.data) - 1
  
          while index > 1:
              curr_index = index
              curr = self.data[index]
  
              index = index // 2
              parent = self.data[index]
  
              if parent < curr:
                  self.data[curr_index], self.data[index] = self.data[index], self.data[curr_index]
  
              else:
                  break
  
      def remove(self):
          if len(self.data) > 1:
              self.data[1], self.data[-1] = self.data[-1], self.data[1]
              data = self.data.pop(-1)
              self.maxHeapify(1)
  
          else:
              data = None
  
          return data
  
      def maxHeapify(self, i):
          left = 2 * i
          right = (2 * i) + 1
          smallest = i
  
          # 왼쪽 자식이 존재하고, 왼쪽 자식의 값이 현재 노드의 값보다 큰 경우
          if left < len(self.data) and self.data[smallest] < self.data[left]:
  
              # smallest 는 왼쪽 자식의 인덱스
              smallest = left
  
          if right < len(self.data) and self.data[smallest] < self.data[right]:
              smallest = right
  
          if smallest != i:
              self.data[i], self.data[smallest] = self.data[smallest], self.data[i]
              self.maxHeapify(smallest)

  
  

• 응용

  1. 우선순위 큐

  2. 힙 정렬(Heap Sort)

     • 시간복잡도가 O(N * log N)

메모

---

• 환형 큐 구현 실습
  • dequeue()할 때 list.pop()이 아니라, 인덱스로 접근해 값을 가져와야 함
    • pop()은 항목의 값이 아닌 항목 자체를 추출하기 때문에 리스트의 길이 감소