! [Java][백준] #14620 - 꽃길

배수연·2024년 4월 12일

Java 백준 알고리즘

algorithm

목록 보기

25/45

🔗 백준 14620 - 꽃길

문제

알고리즘 분류

브루트포스 알고리즘

풀이

1. 입력

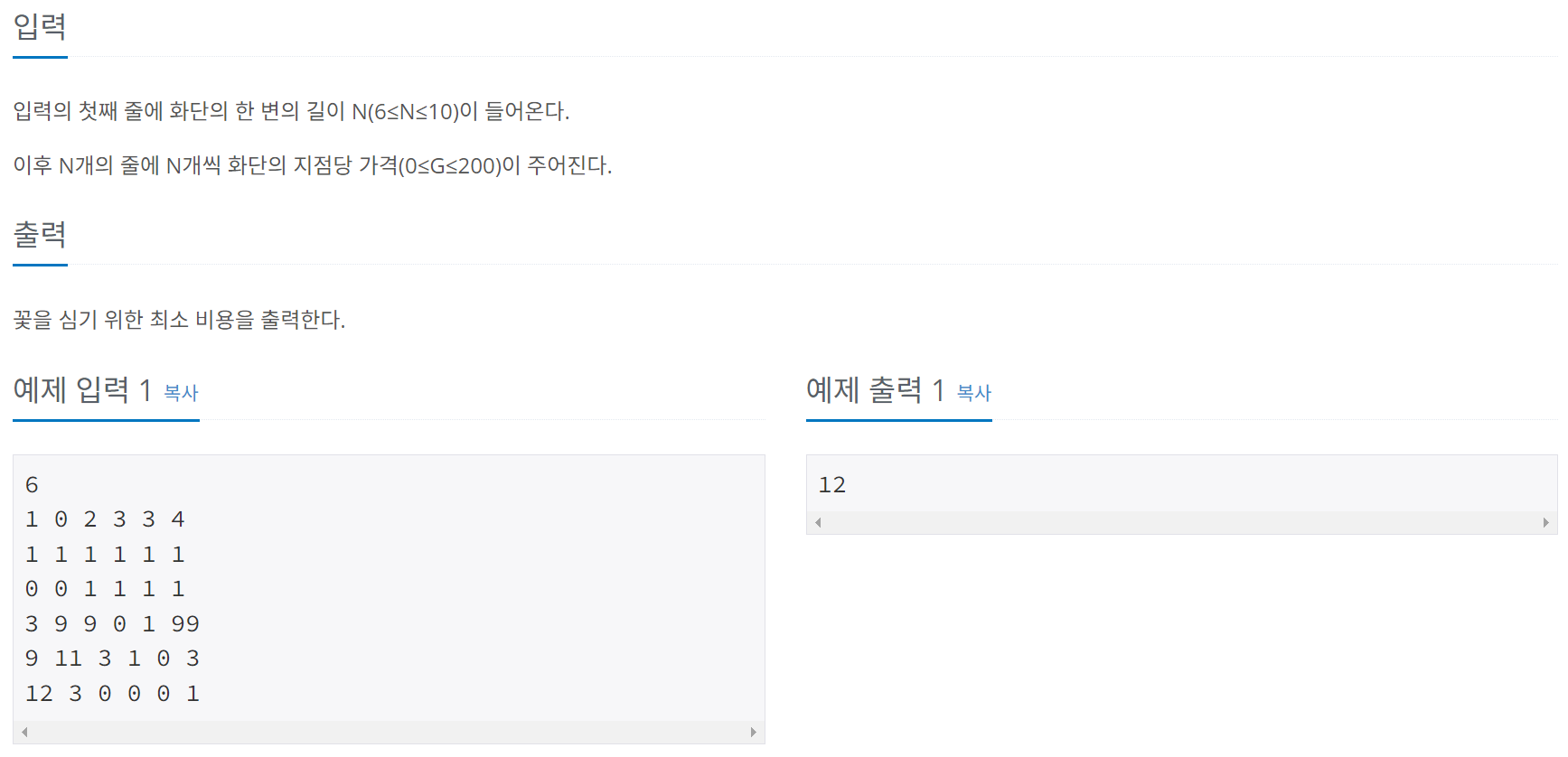
한 변의 크기 n을 입력받아, 비용을 값으로 갖는 n*n 화단 2차원 배열 생성

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        arr = new int[n+1][n+1];
        visited = new boolean[n+1][n+1];

        for(int i=1; i<=n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            for(int j=1; j<=n; j++) {
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

2. 심을 수 있는 칸인지 확인하는 함수 구현

가장 먼저 해당 칸이 이미 방문되었는지 확인
상하좌우 칸이 이미 방문한 칸일 경우, 또는 화단을 벗어나는 경우 false 반환

    public static boolean isPossible(int x, int y) {
        if(visited[x][y]) {
            return false;
        }
        for(int i=0; i<4; i++) {
            int nx = x+dx[i];
            int ny = y+dy[i];
            if(!isRange(nx,ny)) {
                return false;
            }
            if(visited[nx][ny]) {
                return false;
            }
        }
        return true;
    }
    public static boolean isRange(int x, int y) {
        if(x>=1 && y>=1 && x<=n && y<=n) {
            return true;
        }
        return false;
    }

3. 비용 계산 함수

해당 칸과 상하좌우 칸의 비용을 합쳐 저장

    public static int get_sum(int x, int y) {
        int sum = arr[x][y];
        for(int i=0; i<4; i++) {
            int nx = x+dx[i];
            int ny = y+dy[i];
            sum+= arr[nx][ny];
        }
        return sum;
    }

4. set visited 함수 구현

visited로 처리할 지에 대한 여부를 인자로 받아, 해당 칸과 상하좌우 칸의 방문 여부(boolean visited)를 저장

    public static void set_visit(int x, int y, boolean v) {
        if(v) {
            visited[x][y] =true;
            for(int i=0; i<4; i++) {
                int nx = x+dx[i];
                int ny = y+dy[i];
                visited[nx][ny] = true;
            }
        }
        else {
            visited[x][y]= false;
            for(int i=0; i<4; i++) {
                int nx = x+dx[i];
                int ny = y+dy[i];
                visited[nx][ny]= false;
            }
        }
    }

5. 위 함수를 조합한 DFS 함수 구현

먼저, 씨앗이 3개면 최솟값을 비교하여 저장하고 함수를 종료
2차원 배열을 돌면서, 심을 수 있는 칸이라면 그 칸과 상하좌우칸의 비용 합계를 저장함.

    public static void dfs(int seeds,  int sum) {
        if(seeds ==3) {
            min =Math.min(min, sum);
            return;
        }

        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) {
                if(isPossible(i,j)) {
                    int temp = get_sum(i,j);
                    set_visit(i,j,true);
                    dfs(seeds+1,sum+temp);
                    set_visit(i,j,false);
                }
            }
        }

    }

전체 코드

import java.io.*;
import java.util.*;
public class Main {
    static int[][] arr;
    static int n;
    static int min = Integer.MAX_VALUE;
    static int[] dx = {0,0,1,-1};
    static int[] dy = {1,-1,0,0};
    static boolean[][] visited;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        n = Integer.parseInt(br.readLine());
        arr = new int[n+1][n+1];
        visited = new boolean[n+1][n+1];

        for(int i=1; i<=n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            for(int j=1; j<=n; j++) {
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }
        dfs(0,0);
        System.out.println(min);
    }
    public static void dfs(int seeds,  int sum) {
        if(seeds ==3) {
            min =Math.min(min, sum);
            return;
        }

        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) {
                if(isPossible(i,j)) {
                    int temp = get_sum(i,j);
                    set_visit(i,j,true);
                    dfs(seeds+1,sum+temp);
                    set_visit(i,j,false);
                }
            }
        }

    }
    public static int get_sum(int x, int y) {
        int sum = arr[x][y];
        for(int i=0; i<4; i++) {
            int nx = x+dx[i];
            int ny = y+dy[i];
            sum+= arr[nx][ny];
        }
        return sum;
    }
    public static void set_visit(int x, int y, boolean v) {
        if(v) {
            visited[x][y] =true;
            for(int i=0; i<4; i++) {
                int nx = x+dx[i];
                int ny = y+dy[i];
                visited[nx][ny] = true;
            }
        }
        else {
            visited[x][y]= false;
            for(int i=0; i<4; i++) {
                int nx = x+dx[i];
                int ny = y+dy[i];
                visited[nx][ny]= false;
            }
        }
    }
    public static boolean isPossible(int x, int y) {
        if(visited[x][y]) {
            return false;
        }
        for(int i=0; i<4; i++) {
            int nx = x+dx[i];
            int ny = y+dy[i];
            if(!isRange(nx,ny)) {
                return false;
            }
            if(visited[nx][ny]) {
                return false;
            }
        }
        return true;
    }
    public static boolean isRange(int x, int y) {
        if(x>=1 && y>=1 && x<=n && y<=n) {
            return true;
        }
        return false;
    }
}