[Java][백준] #2960 - 에라토스테네스의 체

🔗 백준 2960 - 에라토스테네스의 체

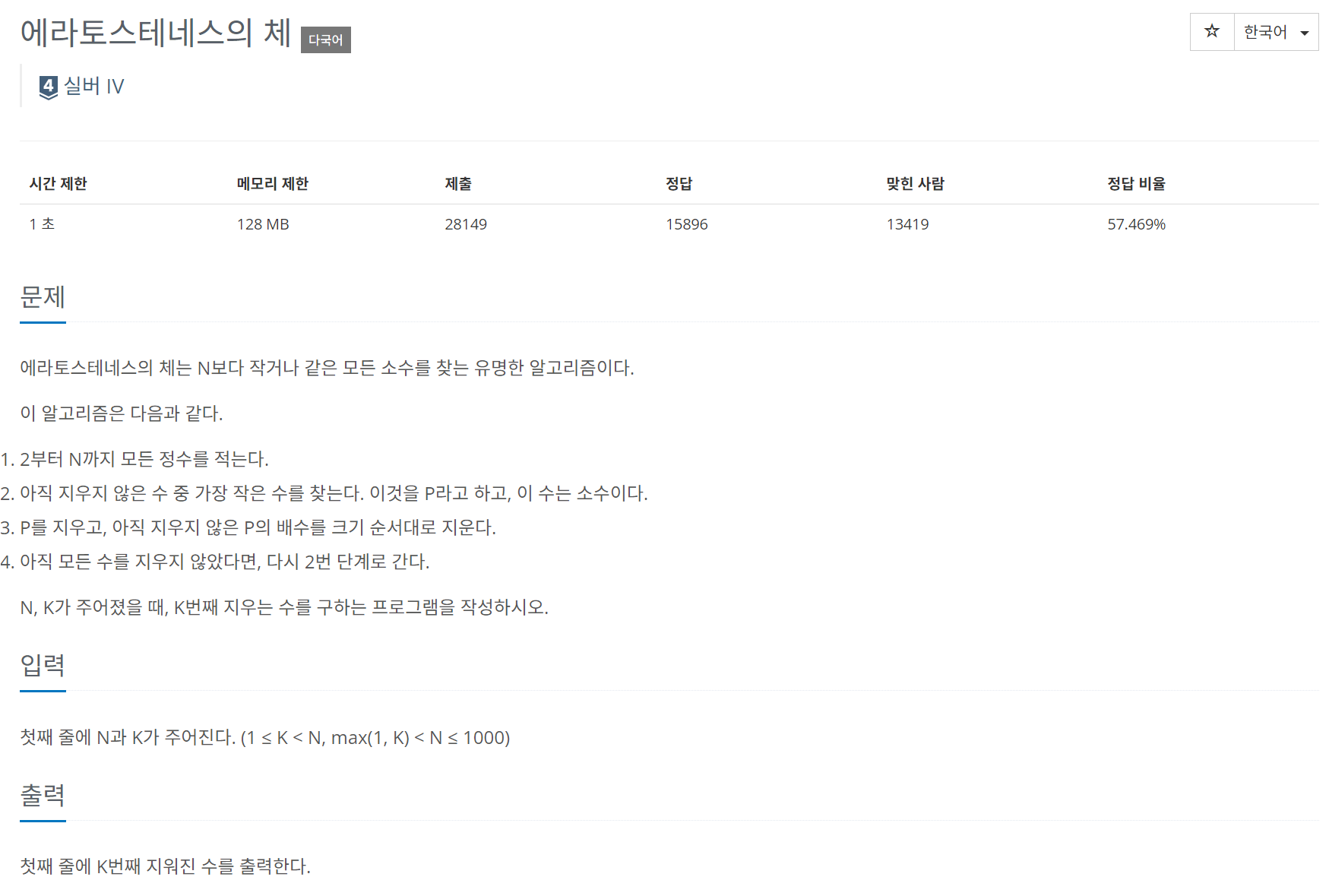
문제

알고리즘 분류

• 수학
• 구현
• 정수론
• 소수 판정
• 에라토스테네스의 체

---

IDEA

• 이 문제에서 주의할 점은, 소수를 찾는 문제가 아니다.
• 이전에 푼 소수구하기 문제와 달리, 이번 문제에서는 소수(2, 3, 5, 7 등)도 지워야 한다.
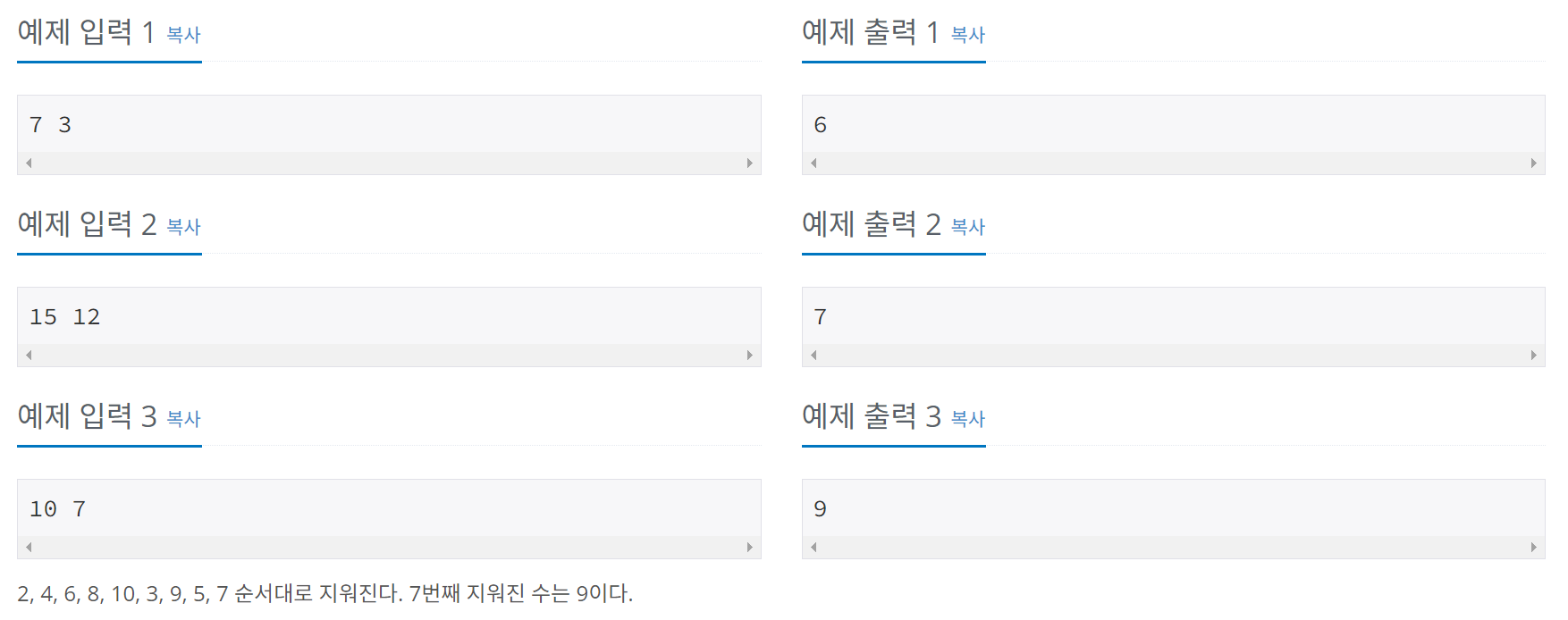
  - 예제 입력 3 아래의 설명을 보면 알 수 있다.

풀이

1. 입력

• 배열에 수 저장

        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        int[] sieve = new int[n+1]; // 배열 설정
        for(int i = 2; i<=n; i++){
            sieve[i] = i;
        }

2. 배수 지우기

• 2부터 시작하는 반복문을 통해 각 수의 배수를 0으로 초기화
• 소수를 구할 때, 2, 3, 5, 7 등 소수'는 지우지 않으나, 해당 문제에서는 소수도 지움
• 수가 지워질 때마다 count를 증가하며, 만약 count가 k와 같을 시 지워지는 수를 출력하고 반복문을 종료

        sieving:
        for(int i = 2; i<=n; i++){
            if (sieve[i] == 0) continue;
//            for(int j = i+i; j<=n; j+=i){ // 원래 소수를 구하던 방식
            for(int j = i; j<=n; j+=i){ // 소수도 삭제하는 방식
                if (sieve[j] == 0) continue;
                count++; // 지울 때마다 count증가
                if(count == k){ // 지워진 수가 k와 같으면
                    System.out.println(sieve[j]); // 출력 후
                    break sieving; // 반복문 종료
                }
                sieve[j] = 0;
            }
        }

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        int[] sieve = new int[n+1]; // 배열 설정
        for(int i = 2; i<=n; i++){
            sieve[i] = i;
        }

        int count = 0;
        sieving:
        for(int i = 2; i<=n; i++){
            if (sieve[i] == 0) continue;
//            for(int j = i+i; j<=n; j+=i){ // 원래 소수를 구하던 방식
            for(int j = i; j<=n; j+=i){ // 소수도 삭제하는 방식
                if (sieve[j] == 0) continue;
                count++;
                if(count == k){
                    System.out.println(sieve[j]);
                    break sieving;
                }
                sieve[j] = 0;
            }
        }
    }
}

• 문제는 어렵지 않았으나 소수를 지우는 걸 몰라서 좀 헤맨 문제.. 제목에 낚였음