Compiler

1. Definition of Compiler

• Translation, 소스코드에 대해서 같은 의미의 실행을 하는 프로그램으로 변환시켜줌.
• 이제는 언어에서 언어로 바꿔줌

2. Characteristics of Compiler

• input language 구조를 이해하고 프로세스를 한다.
• 분석된 구조를 타겟 언어의 형태로 맵핑하는 알고리즘 사용한다. (복잡함)
• compiler : 타겟 코드 만드는데 중요한것은 efficiency이다.
  / interpreter : 즉시 만드는 것은 flexibility를 중요시함.

3. A language-processing system

• (Idea) algorithm -> (Text editor) skeletal source program
  -> (pre-processor) modified source program -> (Compiler) Assembly code
  -> (Assembler) machine code(partial)
  (머신코드를 바로 만들기 힘들어서 어셈블러 만들고 나머지는 다른 친구들한테 시킴.)
  library, relocatable object files
  -> (Linker) absolute machine code

4. The Phases of A Compiler
   

• symbol-table manager 모든 모듈들이 공유하게 한다
• error handler 에러발생시 이를 보내서 핸들시킨다.

5. Lexical Analysis Phase (필수)

• source program file에서 characters 읽기
• Grouping : lexemes or tokens라 불리는 chunks로 characters 묶기
• 토큰은 keyword, constant, operator, identifier, etc라는 logically cohesive sequence of character
• lexer(or scanner)에 의해 수행이 되고, 여기서는 efficiency가 가장 중요 관점

6. Syntax Analysis Phase (필수)

• 그룹된 것을 계층적(hierarchically)으로 그룹화 시킴
• Intermediate repesentation 인 AST( Abstract Syntax tree)로 구성
• Performed by a parser
• Syntax Analysis Phase : Parse Tree
  

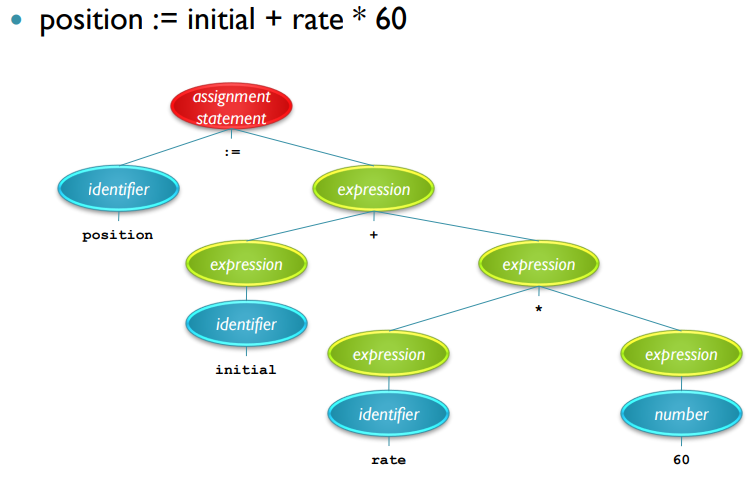
7. Semantic Analysis Phase

• 잘 되어있는지 check
• 대부분은 parser가 하지만, 몇몇은 done by lexer or code generator
• 이 수행자 is called constrainer by pittman
• Type checking, uniqueness

8. Intermediate Representation

9. Code optimization

• Reducing execution time
• Saving memory space
• Reducing communication bandwidth

10. Code Generation Phase (필수)

• 중간표현이나 어셈블리 코드를 마지막으로서 target code로 만드는 과정

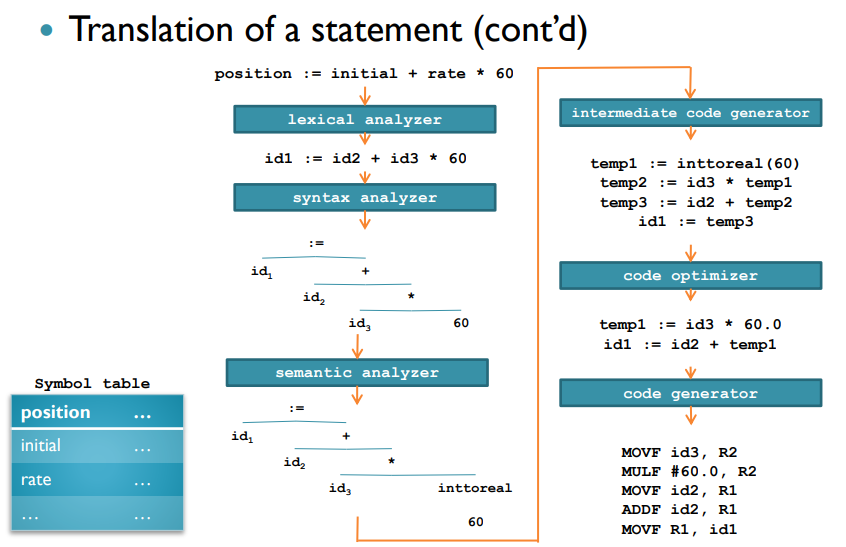
Grammar

1. Basic concepts

• 정해진대로 써야함
• 4가지로 구성 되어있음 (∑, N, P, S)
• ∑ 변할 수 없는 terminal symbols
• nonterminal symbols는 변할 수 있고 이는 N안에 있음
• proguction rules P에 적혀있음 (알파가 베타로 변할 수 있다)
• goal symbol S is the start symbol

2. 계산기 grammar

G = (∑, N, P, S) where
∑ = {n, +, \*, (, )}, // 이 5개만 쓸 수 있다.
N = {E, T, F},  // 다른것로 바꿀 수 있는 것들
P = {E → E + T, E → T, T →T * F, T → F, F → (E), F → n } // 바뀔 수 있다는 공식들 모음
S = E // 그 중에 E를 스타트 심볼로 정의하자

3. String

• terminal or zero로 이루어진 것

4. Language

• A set of strings
• mathematically L(G) = { ω | ω ∈ ∑ and S => ω}
• if L(G1) = L(G2) -> G1 and G2 are equivalent

G1 = { {a, b, c}, / terminals / 
{A, B} / non-terminals / 
{A ➔ aB, A ➔ bB, A ➔ cB, B ➔ a, B ➔ b, B ➔ c}, 
S / start symbol / } 
L(G1) = { aa, ab, ac, ba, bb, bc, ca, cb, cc}

5. Derivation

• A -> bB -> bc (two immediate derivations)
  could be summarized as A ->* bc

• Derive n + n * n using G2
  답변이 yes면 만들 수 있다, no면 만들 수 없다.
  If E ➔ n + n n is possible(at least one path to produce the string), then
  we say that “string n + n * n can be derived from E using G2” or n + n *
  n ∈ L(G2)
  
  grammacty collectly 하다!

• Parse Tree from n+n*n using G2
  
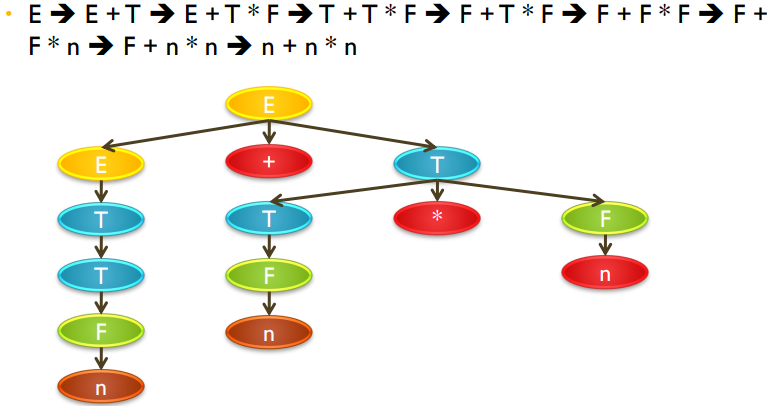
  순차과정은 Top down, 역순은 Bottom up

6. Terms for Grammar and Derivation Methods

• non terminal -> terminal로 만들어야함
• Rightmost derivation (Bottom up) vs. Leftmost derivation (Top down : start symbol 부터 시작함.)
  Rigghtmost : 오른쪽부터 없애는 것 위 예시 그림
• Ambiguous grammar
  왼쪽부터랑 오른쪽부터랑 결과가 다를때 쓸모가 없음 (트리가 달라지면)
  
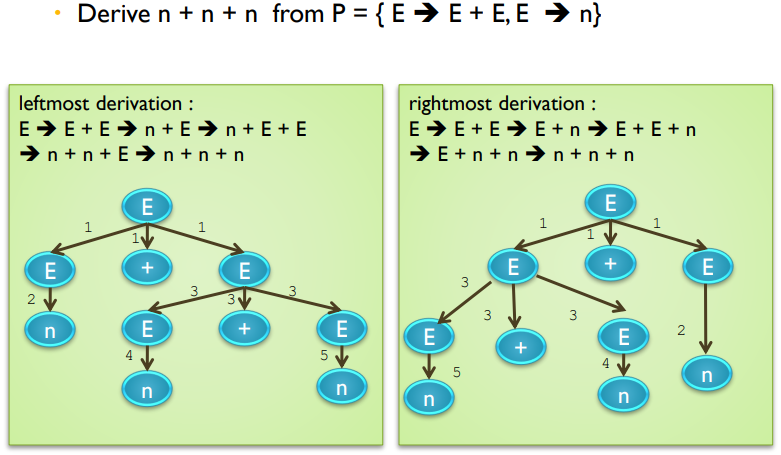
  3-2-5 = 6 / 3-2-5=-4