Introduction

• scanner
  Stripping out from the source program the comments and white spaces
  Reading in input characters and grouping them into tokens
  Correlating error messages from the compiler with the source program

• 파서로부터 lexical analysos phase 분리 이유
  Simpler design
  Parser does not care about comments, white space
  Improved compiler efficiency
  Specialized buffering technique
  Enhanced Portability
  Input peculiarities are restricted to lexical analyzer
  Better software engineering
  Debugging and maintenance
  

• Three approaches to implemnet lexical analysis
  1) Use a tool to produce lexical analyzer from the specification based on regular expression
  2) Write a lexical analyzer in a conventional systems programming language
  3) Write a lexical analyzer in assembly language
  

Regular Expression

1. Definition
   Ф is a RE and denotes the empty set : A set containing nothing
   ε is a RE and denotes {ε} : A set containing empty string
   A single character in ∑ is a RE (denotes {a} if a ∈ ∑)
   Suppose r and s are regular expressions denoting L(r) and L(s),

   r | s is a RE denoting L(r) ⋃ L(s) : sometimes said r + s
   r s is a RE denoting L(r) L(s)
   r* is a RE denoting (L(r))* (repeating)
   (r) is a RE denoting L(r) with extra parenthesis

2. Example
   (0 | 1)* : all strings of 1 and 0
   (1 | 10)* : all strings of 0's and 1's beginning with 1 and no consecutive 0's appear

   <수학적 귀납법으로 증명 가능>
   ① Say the general form is (1 | 10)i
   ② Base case : For i = 0 and 1, it is true and ε and (1 | 10)
   respectively
   ③ Induction Hypothesis : Suppose it is true for i = n, (1 | 10)n
   ④ show that it is also true for n + 1, that is, (1 | 10)n+1
   ⑤ (1 | 10)n+1 = (1 | 10)n
   (1 | 10) = (1 | 10)n 1 or (1 | 10)n 10
   ⑥ Thus, it is true for all n

3. Conventions in specifying the regular expressions
   

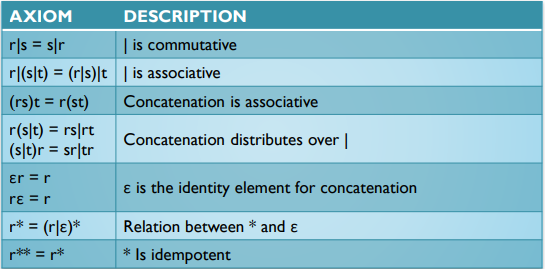
4. Examples : Let ∑ = {0, 1}
   The regular set denoted by the regular expressions a | b?
   {a, b}
   The regular set denoted by the regular expressions (a | b)(a | b)?
   {aa, ab, ba, bb}
   The regular set denoted by the regular expressions (a | b)*?
   {all strings containing zero or more instances of a and b's}
   The regular set denoted by the regular expressions a | a* b?
   {a, strings containing zero or more a's followed by b}
   {a, b, ab, aab, aaab, ... }

5. Non regular sets : regular expression not exist(No memory).
   L = { ωcω | ω is a string of a's and b's} - repeated string
   {abcab, aabbcaabb, aabcaab, ababcababc}

6. 

7. Transforming regular expression into regular grammar

   1. Introduce a start symbol
      w : A → w
   2. Remove meta symbols
      A → xy : A → xB B → y
   3. Remove Kleene star
      A → x*y : A → xB A → y B → xB B → y
   4. Union
      A → x | y : A → x A → y
   5. Eliminating redundancy
      A → B B → x : A → x B → x
   6. Empty production
      A → ε B → xA : B → xA B → x

   8.
   입실론? 빠지면 명백히 표시해야하지않나?
   9.

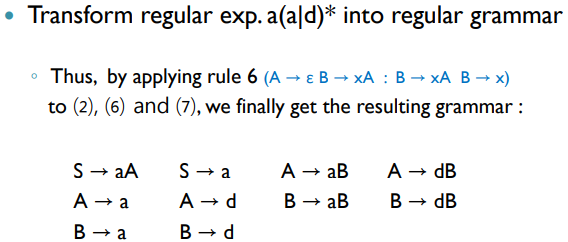
   10.

Finite State Automata

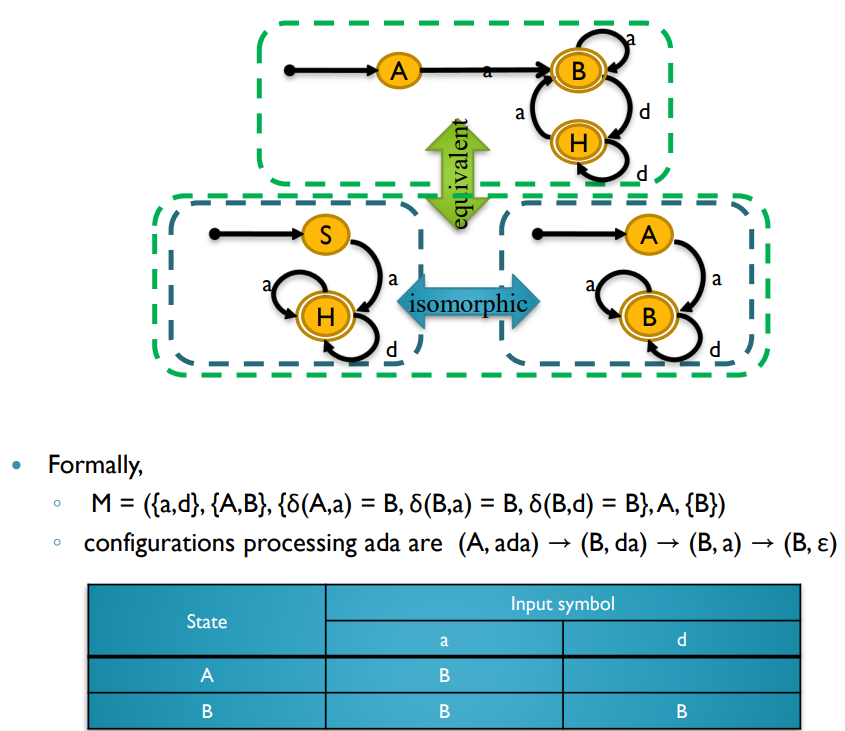
1. Def : Nondeterministic Finite-State Automata
   M = (∑, Q, Δ, q0, F) where
   ∑ is a set of all strings in the specification of regular expressions
   Q is a finite set of states
   Δ is a set of transition rules saying that how the automaton advances from one
   state to next for the input tape
   Thus Δ : Q x ∑ → Q
   q0 is the start state and
   F is the set of final states.

   Def : Configuration
   ◦ (q, ω) where current state q ∈ Q and the rest of input string ω∈ ∑*
   ◦ If an automaton is in (q, ε) where q ∈ F then FSA accepts the string;
   otherwise, the string is rejected by the FSA

2. 

3. 

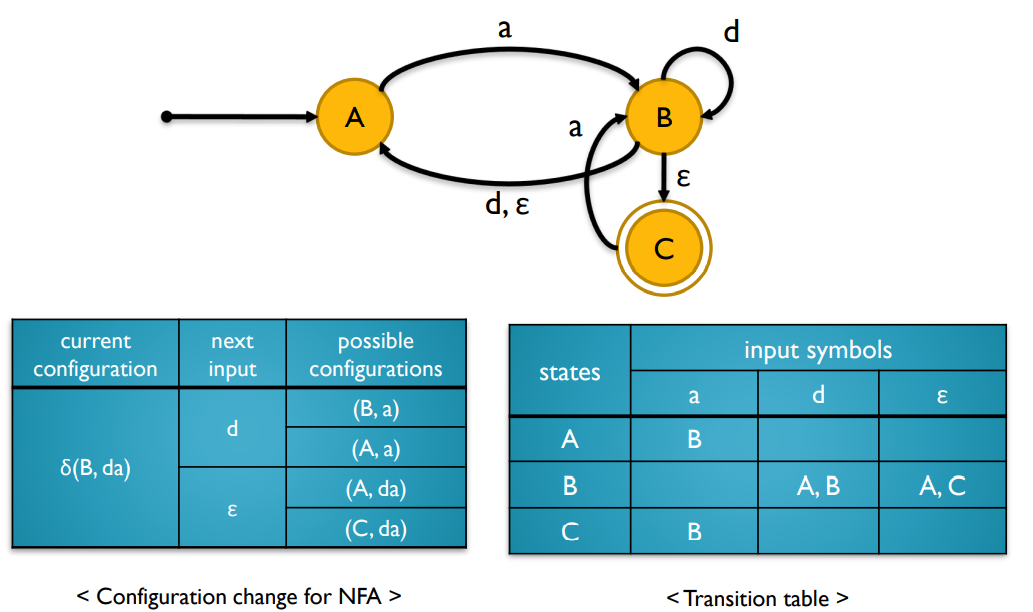
4. S → aA , A → b | a
   ({a,b}, {S,A,F}, {δ(S, a) = A, δ(A, a) = F, δ(A, b) = F}, S, {F})
   

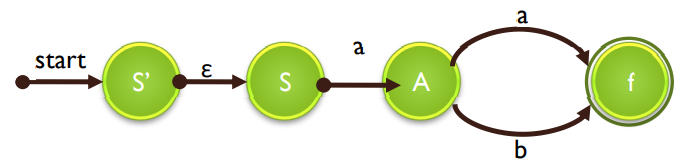
5. Transforming regular expression to NFA (Thomson's construction)
   1) For ε, construct the NFA
   2) For a in Σ, construct the NFA
   3) For N(s) and N(t) are NFAs for s and t, then
   a. N(s|t) is (for s|t)
   b. N(st) is (for st)
   c. N(s) is (for s)
   d. N((s)) is (for (s)) same as N(s)

6. 

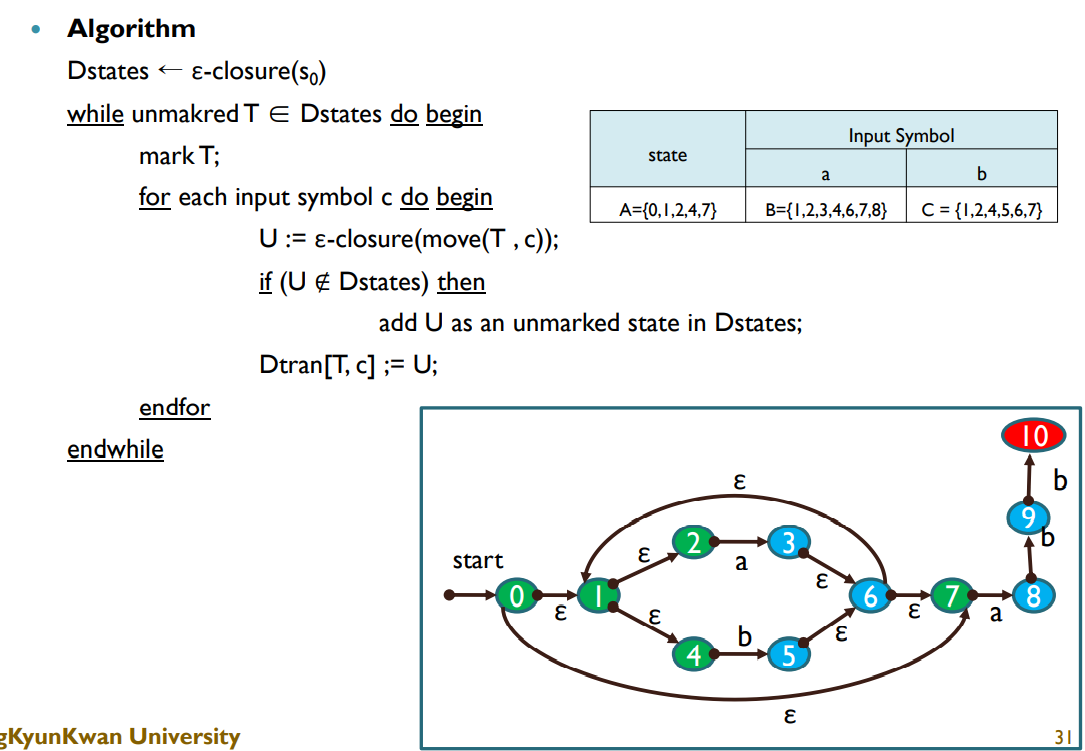
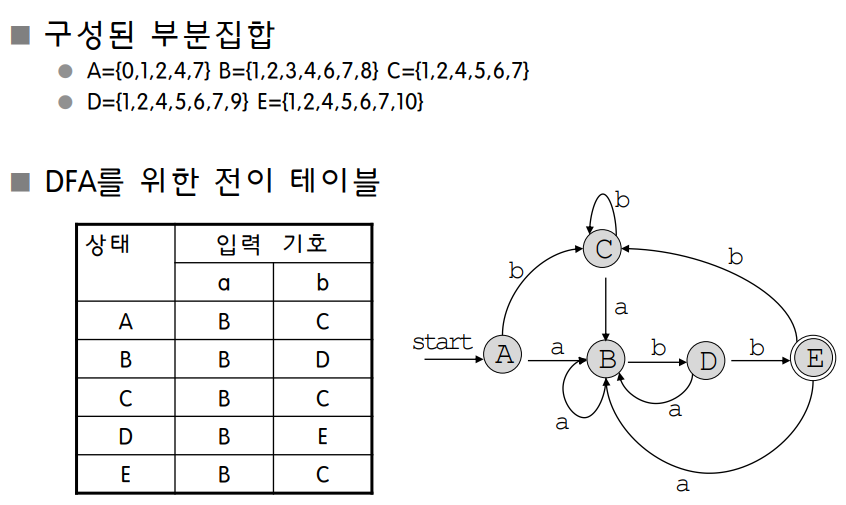
7. 부분집합 구성 알고리즘 예
   
   

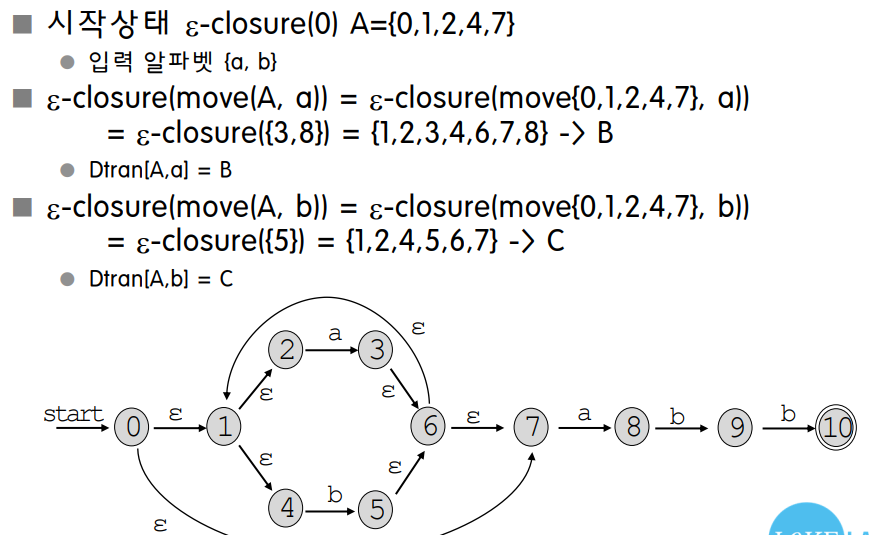
8. FA에서 상태수를 줄이는 방법
   Find all group of states that can be distinguished by some input string
   Each group that cannot be distinguished is then merged into a single state
   Merge A and C and make A as a representative

reference : http://contents.kocw.or.kr/document/lec/2012/ChungBuk/LeeJaeSung/cp-11.pdf