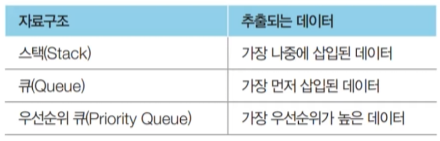
💡 우선순위큐
우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조 (우선순위에 따라 처리하고 싶을 때 사용)
우선순위 큐를 구현하는 방법
- 리스트를 이용하여 구현
class PriorityQueue {
constructor() {
this.items = [];
}
//[{ element: 'a', priority: 5 }, { element: 'b', priority: 2 }, { element: 'c', priority: 3}}]
// [ "B", "C", "A"]의 순서로 큐가 정렬되어야 함
enqueue(element, priority) { // 큐의 맨 뒤에 item을 추가 // 시간복잡도 O(n)
const item = { element, priority };
let added = false; // added가 true가 되면 for문을 빠져나감 (중요도가 높은 item이 큐의 앞에 위치하게 됨)
for ( let i =0; i < this.items.length; i++){
// itesm[0] = { element: 'a', priority: 5 }
// input item = { element: 'b', priority: 2 }
// [ ..., (input) { element: 'b', priority: 2 }, (shift){ element: 'a', priority: 5 }, ...]
if (item.priority < this.items[i].priority){
this.items.splice(i, 0, item); // i번째에 item을 추가하고, 기존 i번째부터 뒤로 한칸씩 밀어냄
added = true; // for문을 빠져나가기 위한 flag
break;
}
}
if (!added) { // for문을 빠져나가지 않았다면, added는 false
this.items.push(item); // for문을 빠져나가지 않았다면, 큐의 맨 뒤에 item을 추가
}
}
dequeue() { // 큐의 맨 앞에 있는 item을 반환하고, 큐에서 삭제 // 시간복잡도 O(1)
if (!this.isEmpty()) {
return this.items.shift(); // 큐의 맨 앞에 있는 item을 반환하고, 큐에서 삭제
} else {
return "Queue is empty!"; // 큐가 비어있다면, 에러 메시지 출력 후 종료 (원래는 NULL을 반환해야 함)
}
}
peek() { // 큐의 맨 앞에 있는 item을 반환 // 시간복잡도 O(1)
if (!this.isEmpty()) {
return this.items[0]; // 큐의 맨 앞에 있는 item을 반환
} else {
return "Queue is empty!"; // 큐가 비어있다면, 에러 메시지 출력 후 종료 (원래는 NULL을 반환해야 함)
}
}
isEmpty() { // 큐가 비어있는지 확인 시간복잡도 O(1)
return this.items.length == 0; // 큐의 길이가 0이면 비어있는 것
}
clear() { // 큐를 비움 시간복잡도 O(1)
this.items = [];
}
printQueue() { // 큐를 출력 시간복잡도 O(n)
return this.items.map((item) => `${item.element} : ${item.priority}`);
}
sizeOfQueue() { // 큐의 길이를 반환 // 시간복잡도 O(1)
return this.items.length;
}
}
let myqueue = new PriorityQueue();
myqueue.enqueue("A", 5);
console.log(myqueue.printQueue());
myqueue.enqueue("B", 2);
console.log(myqueue.printQueue());
myqueue.enqueue("C", 3);
console.log(myqueue.printQueue());
myqueue.enqueue("D", 1);
console.log(myqueue.printQueue()); // D,B,C,A
myqueue.dequeue();
console.log(myqueue.printQueue()); // B,C,A- 힙을 이용하여 구현
class PriorityQueue {
constructor() {
this.heap = [null]; // 인덱스 0은 사용하지 않기 위해 null을 넣어준다.
// 인덱스 1부터 사용하기 위해 null을 넣어준다.
}
/**Heap
* left child = parent * 2
* right child = parent * 2 + 1
* parent = child / 2
*/
insert(value) {
this.heap.push(value);
// 힙의 길이가 2 초과면 (힙의 길이가 2이면 1개만 들어있는 것이므로 비교할 필요가 없다.)
if (this.heap.length > 2) {
// 힙의 마지막 인덱스의 부모 인덱스를 구한다. (Math.floor(this.heap.length / 2)는 마지막 인덱스의 부모 인덱스이다.
// parent = child / 2
// current는 마지막 추가된 인덱스이다.
let current = this.heap.length - 1;
// 만약 비교해봤을 때 부모 인덱스의 값이 자식 인덱스의 값보다 크다면
while (this.heap[current] < this.heap[Math.floor(current / 2)]) {
// 부모 인덱스와 자식 인덱스의 값을 바꿔준다.
if (current >= 1) {
// 배열 구조 분해 할당
// [a, b] = [b, a] => a와 b의 값을 바꿔준다.
// 자식 인덱스와 부모 인덱스의 값을 바꿔준다.
// heap[current] = 자식 인덱스의 값
// heap[Math.floor(current / 2)] = 부모 인덱스의 값
[
([this.heap[Math.floor(current / 2)], this.heap[current]] = [
this.heap[current],
this.heap[Math.floor(current / 2)],
]),
];
// 부모 인덱스로 이동한다.
// 부모노드가 Root노드가 아니라면
if (Math.floor(current / 2) > 1) {
// current는 부모 인덱스로 이동한다.
current = Math.floor(current / 2);
} else {
break;
}
}
}
}
}
remove() {
if (this.heap.length <= 1) return null;
// 최소값은 루트 노드이다.
const minValue = this.heap[1];
this.heap[1] = this.heap.pop();
// 초기값
let current = 1;
let leftChild = current * 2;
let rightChild = current * 2 + 1;
// 왼쪽 자식이나 오른쪽 자식이 현재 값보다 작으면 계속 실행
while (this.heap[leftChild] < this.heap[current] || this.heap[rightChild] < this.heap[current]) {
// 왼쪽 자식이나 오른쪽 자식이 없으면 break
if (!this.heap[leftChild] || !this.heap[rightChild]) break;
// 왼쪽 자식이 오른쪽 자식보다 작으면 왼쪽 자식과 현재 값을 바꿔준다.
if (this.heap[leftChild] < this.heap[rightChild]) {
// 배열 구조 분해 할당
[this.heap[current], this.heap[leftChild]] = [this.heap[leftChild], this.heap[current]];
// 현재 위치를 왼쪽 자식으로 바꿔준다.
current = leftChild;
} else {
// 오른쪽 자식이 왼쪽 자식보다 작으면 오른쪽 자식과 현재 값을 바꿔준다.
[this.heap[current], this.heap[rightChild]] = [this.heap[rightChild], this.heap[current]];
// 현재 위치를 오른쪽 자식으로 바꿔준다.
current = rightChild;
}
// 왼쪽 자식과 오른쪽 자식의 인덱스를 다시 구한다.
leftChild = current * 2;
rightChild = current * 2 + 1;
console.log(this.heap);
}
// 최소값을 반환한다.
return minValue;
}
peek() {
// 최소값은 루트 노드를 반환한다..
return this.heap[1];
}
print() {
return this.heap;
}
isEmpty() {
return this.heap.length <= 1;
}
}
const pq = new PriorityQueue();
pq.insert(5);
console.log(pq.print());
pq.insert(3);
console.log(pq.print());
pq.insert(8);
console.log(pq.print());
console.log(pq.remove());
console.log(pq.print());
console.log(pq.peek());
(단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일 (힙정렬)) => O(NlogN)
✔ 힙 Heap
-
완전 이진트리 자료구조의 일종
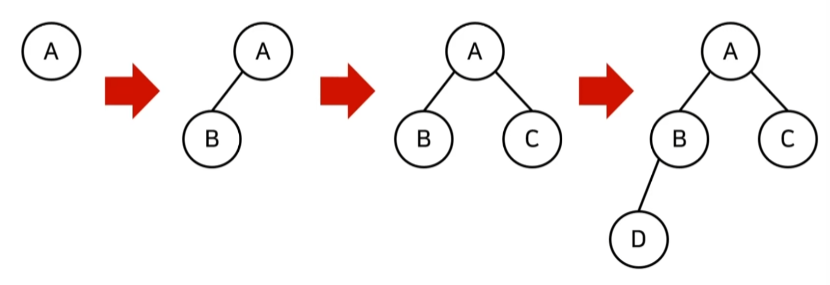
- 루트 노드부터 시작하여 왼쪽 자식 노드, 오른쪽 자식 노드 순서대로 데이터가 차례대로 삽입되는 tree -
힙에서는 항상 루트노드(Root Node)를 제거
최소 힙 (min heap)
- 루트 노드가 가장 작은 값을 가짐
- 값이 작은 데이터가 우선적으로 제거
-
Min-Heapify() 최소 힙 구성 함수
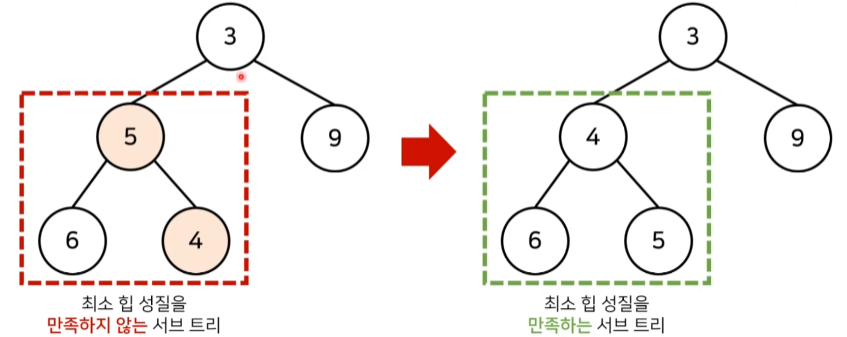
: (상향식) 부모 노드로 거슬러 올라가며, 부모보다 자신의 값이 더 작은 경우에 위치를 교체 -
삽입
새로운 원소가 삽입되었을 때 O(logN)
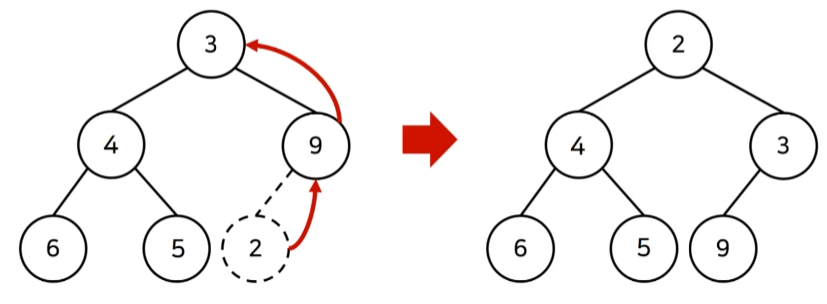
- 제거
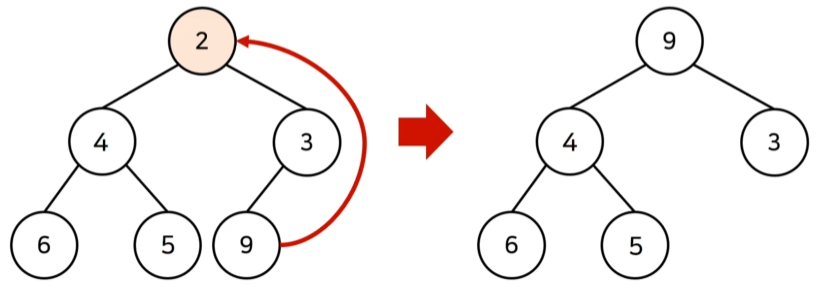
원소를 제거했을 때 O(logN)
: 가장 마지막 노드가 루트 노드의 위치에 오도록 함 (min-heapify 실행)
- 최대 힙 (max heap)
- 루트 노드가 가장 큰 값을 가짐
- 값이 큰 데이터가 우선적으로 제거
- 최소 힙의 반대로 작용
✅ 힙 정렬을 사용하는 이유
❓ 힙 정렬이 왜 필요할까..??
트리안에서 특정 노드 때문에 최대(최소) 힙이 붕괴되는 경우가 있기 때문
(위쪽으로 보았을 때는 최대힙, 아래쪽으로 보았을 때는 최대힙 형성 ❌)
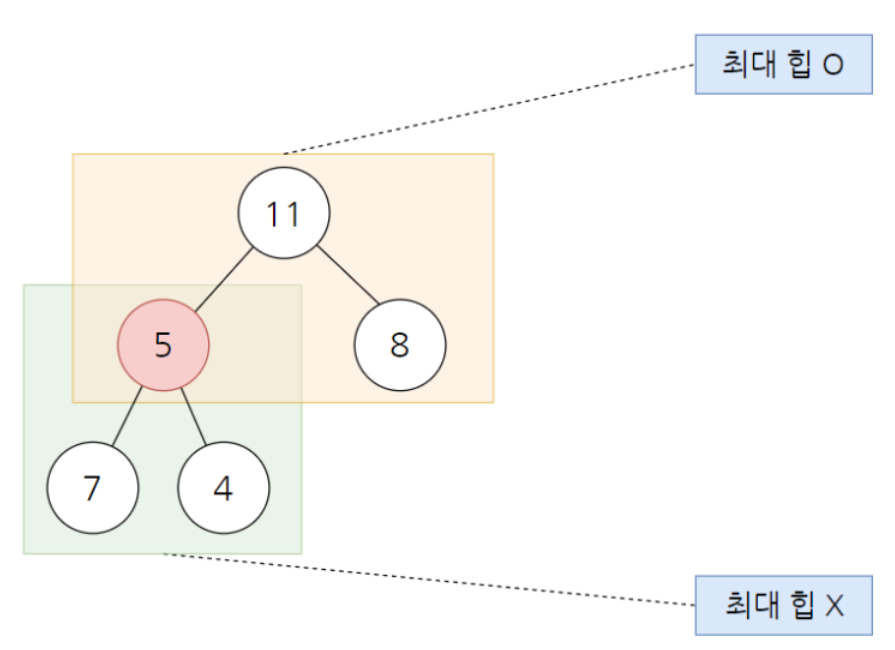
이러한 문제를 해결하기 위해서 힙 생성 알고리즘 (Heapify Algorithm)을 사용
: 특정한 하나의 노드에 대해서 수행하는 것
해당 하나의 노드를 제외하고는 최대 힙이 구성되어 있는 상태를 가정
(해당 예시에서는 5만 최대 힙정렬을 수행해주면 전체 트리가 최대 힙 구조로 형성)
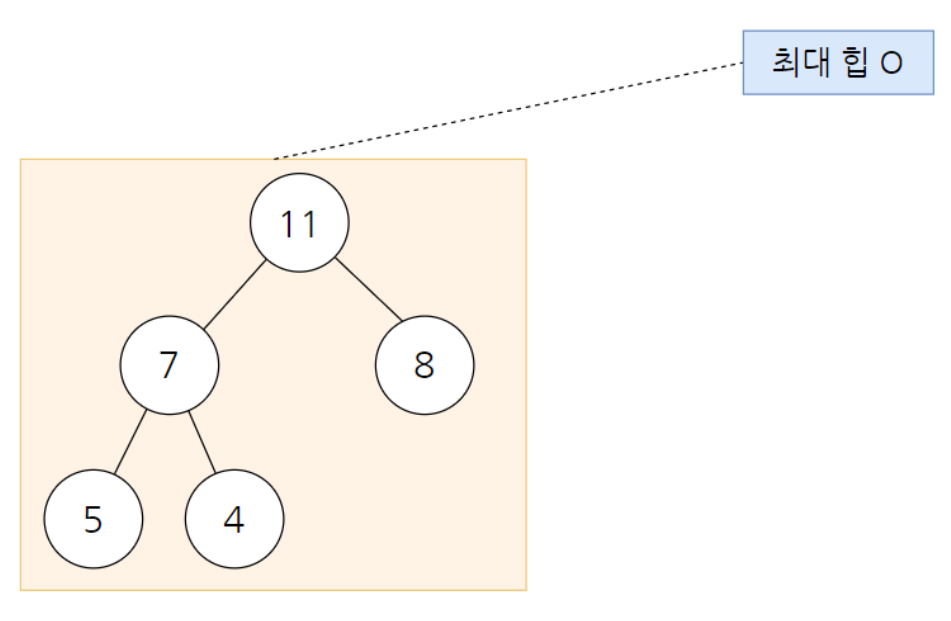
힙 생성알고리즘 (Heapify Algorithm)은 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 알고리즘
출처
즉 전체 데이터의 개수가 N개일 때의 시간 복잡도는 O(N log N)
( **O(전체 데이터의 개수 힙 생성 알고리즘의 시간 복잡도)** )
❓ 힙 정렬을 사용하는 이유
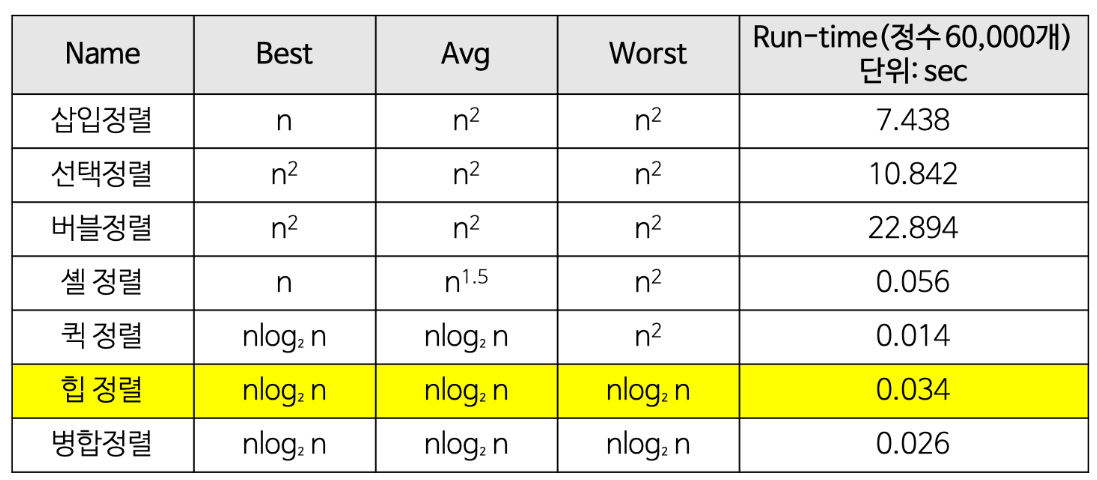
- 장점
- 시간복잡도가 좋다
- 전체 자료를 정렬하는 것이 아니라 가장 큰(작은) 값 몇개만 필요로 할 때 사용할 수 있다.
-
시간복잡도
-
힙트리의 전체 높이가 거의 log2n(완전 이진 트리)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 log2n만큼 소요
-
요소의 개수가 n개 이므로 전체적으로 O(nlog2n)의 시간이 걸림.
-
시간복잡도 => O(nlogn)
-
✅ 다익스트라 알고리즘으로 둘의 차이 알아보기
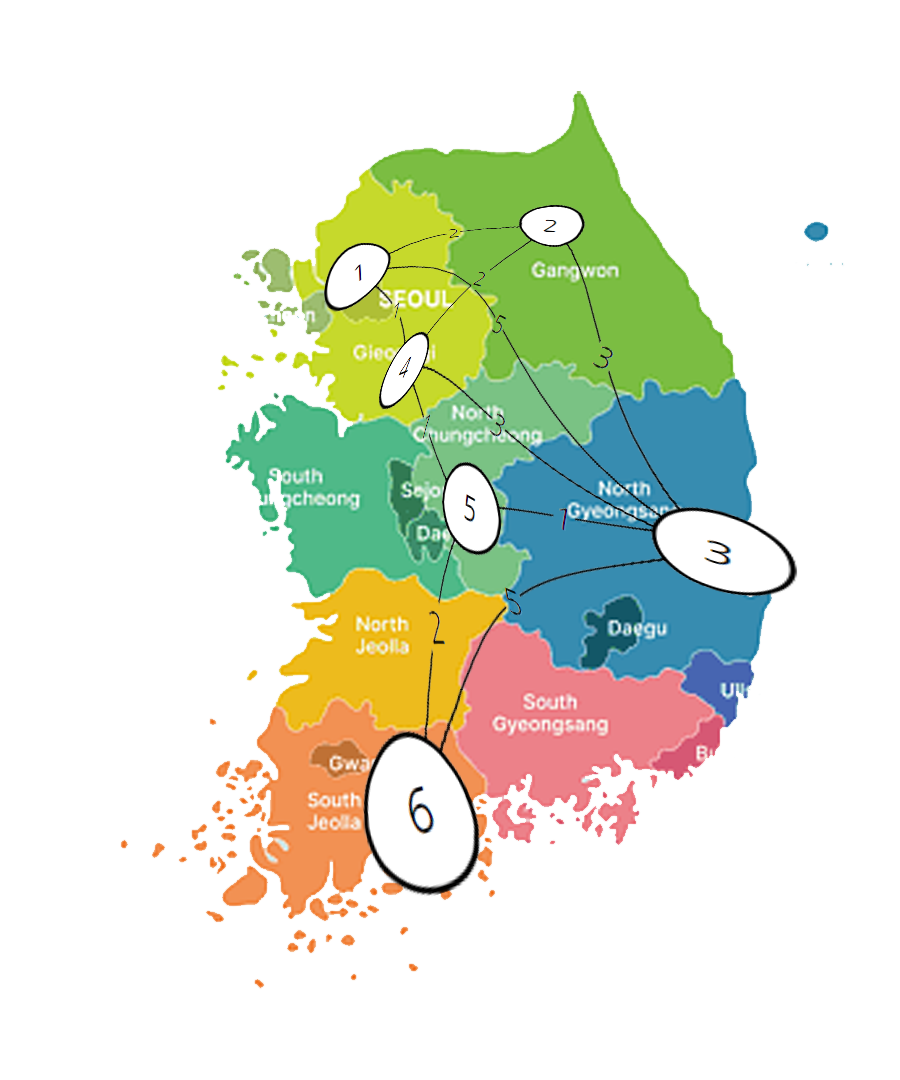
다음과 같은 상황이 있다.
서울에서 각 지역으로 가는 최단거리를 구해서 배열에 넣는 것을 목표로 한다.
❓ 선형 탐색(배열)을 이용한 구현
function dijkstra(그래프, 시작정점) {
// 찍고 찍고 찍고 가야할 위치의 수 (예를들어 서울 대구 대전 광주 부산이라면 5개))
const 정점수 = 그래프.length;
// 가지 않은 곳은 무한대로 설정
// 시작 정점 외의 모든 정점에 대한 초기 거리가 무한대로 설정되면, 그래프의 모든 간선을 고려하지 않고도 알고리즘이 올바르게 작동
// 만약 그래프의 특정 정점에 도달할 수 없는 경우, 해당 정점까지의 거리는 초기값인 무한대로 유지
const 거리 = Array(정점수).fill(Infinity); // 시작 정점에서 각 정점까지의 최단 거리
const 방문 = Array(정점수).fill(false); // 각 정점의 방문 여부
const 지역이름 = ['서울', '원주', '포항', '수원', '대전', '여수'];
거리[시작정점] = 0; // 시작 정점에서 자기 자신까지의 거리는 0 (나에서 나로 이동하니까)
for (let i = 0; i < 정점수 - 1; i++) {
// 정점수 - 1 만큼 반복 (예를들어 5개의 정점이면 4번 반복) -1을 하는 이유는 시작 정점은 이미 거리가 0이기 때문에
let u = 최소거리찾기(거리, 방문);
console.log(`다음 여행지로 ${지역이름[u]}를 선택함`);
방문[u] = true;
for (let v = 0; v < 정점수; v++) {
if (!방문[v] && 그래프[u][v] !== 0 && 거리[u] !== Infinity && 거리[u] + 그래프[u][v] < 거리[v]) {
console.log(
`${지역이름[u]}에서 ${지역이름[v]}로 가는 거리를 파악해보자: ${
거리[u] + 그래프[u][v]
} (원래 거리: ${거리[v]})`,
);
거리[v] = 거리[u] + 그래프[u][v]; // 최단 거리 업데이트
}
}
console.log('-------------------');
console.log('거리: ', 거리);
지역이름.forEach((지역, 인덱스) => console.log(`${지역}: ${거리[인덱스]}`));
console.log('방문 방법을 확정 지은 곳: ', 방문);
console.log('-------------------');
}
return 거리;
}
function 최소거리찾기(거리, 방문) {
console.log('최소 거리 찾기 시작');
let 최소값 = Infinity;
let 최소인덱스 = -1; // 최소값을 가진 정점의 인덱스
// 방문하지 않은 정점 중 최소 거리를 가진 정점을 찾는다.
for (let v = 0; v < 거리.length; v++) {
// 방문하지 않았고, 거리가 최소값보다 작으면
if (방문[v] === false && 거리[v] <= 최소값) {
// 최소값을 거리로 설정하고 최소인덱스를 v로 설정
최소값 = 거리[v];
최소인덱스 = v;
} else {
}
}
return 최소인덱스; // 방문하지 않은 정점 중 최소 거리를 가진 정점의 인덱스 반환
}
// 예제 사용법:
const 그래프 = [
[0, 2, 5, 1, Infinity, Infinity],
[2, 0, 3, 2, Infinity, Infinity],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, Infinity],
[Infinity, Infinity, 1, 1, 0, 2],
[Infinity, Infinity, 5, Infinity, 2, 0],
];
const 시작정점 = 0;
const 최단거리 = dijkstra(그래프, 시작정점);
const 지역이름 = ['서울', '원주', '포항', '수원', '대전', '여수'];
console.log(`시작 정점(${지역이름[시작정점]})에서 다른 모든 정점까지의 최단 거리:`, 최단거리);- 시간복잡도 : O(V^2), V는 정점의 수
- 모든 정점을 순회하면서 최단거리를 업데이트 함
- 각 정점을 선택하는데 O(V)의 시간, 선택된 정점과 연결된 간선을 검사하는데에도 O(V)의 시간
❓ 힙을 이용한 구현
function MinHeap() {
this.heap = [];
this.insert = function (value) {
this.heap.push(value);
this.bubbleUp();
};
this.bubbleUp = function () {
let index = this.heap.length - 1;
const current = this.heap[index];
while (index > 0) {
const parentIdx = Math.floor((index - 1) / 2);
const parent = this.heap[parentIdx];
if (parent.거리 <= current.거리) break;
this.heap[parentIdx] = current;
this.heap[index] = parent;
index = parentIdx;
}
};
this.extractMin = function () {
const min = this.heap[0];
const end = this.heap.pop();
if (this.heap.length > 0) {
this.heap[0] = end;
this.sinkDown();
}
return min;
};
this.sinkDown = function () {
let idx = 0;
const length = this.heap.length;
const element = this.heap[0];
while (true) {
const leftChildIdx = 2 * idx + 1;
const rightChildIdx = 2 * idx + 2;
let leftChild, rightChild;
let swap = null;
if (leftChildIdx < length) {
leftChild = this.heap[leftChildIdx];
if (leftChild.거리 < element.거리) {
swap = leftChildIdx;
}
}
if (rightChildIdx < length) {
rightChild = this.heap[rightChildIdx];
if (
(swap === null && rightChild.거리 < element.거리) ||
(swap !== null && rightChild.거리 < leftChild.거리)
) {
swap = rightChildIdx;
}
}
if (swap === null) break;
this.heap[idx] = this.heap[swap];
this.heap[swap] = element;
idx = swap;
}
};
}
function dijkstra(그래프, 시작정점) {
const 정점수 = 그래프.length;
const 거리 = Array(정점수).fill(Infinity);
const 힙 = new MinHeap();
const 지역이름 = ['서울', '원주', '포항', '수원', '대전', '여수'];
거리[시작정점] = 0;
힙.insert({ 정점: 시작정점, 거리: 거리[시작정점] });
while (힙.heap.length > 0) {
console.log('힙에서 현제 확정지은 거리의 수 : ' + (지역이름.length - 힙.heap.length));
const 현재 = 힙.extractMin();
const 현재정점 = 현재.정점;
const 현재거리 = 현재.거리;
if (거리[현재정점] < 현재거리) continue;
console.log(`다음 여행지로 ${지역이름[현재정점]}를 선택함`);
for (let i = 0; i < 정점수; i++) {
if (그래프[현재정점][i] !== 0 && 그래프[현재정점][i] !== Infinity) {
const 새거리 = 현재거리 + 그래프[현재정점][i];
if (새거리 < 거리[i]) {
console.log(
`${지역이름[현재정점]}에서 ${지역이름[i]}로 가는 거리를 파악해보자: ${새거리} (원래 거리: ${거리[i]})`,
);
거리[i] = 새거리;
힙.insert({ 정점: i, 거리: 새거리 });
}
}
}
console.log('-------------------');
console.log('거리: ', 거리);
지역이름.forEach((지역, 인덱스) => console.log(`${지역}: ${거리[인덱스]}`));
console.log('-------------------');
console.log('최소 힙을 구하고 있습니다.');
console.log('-------------------');
힙.heap.forEach((정점) => console.log(`${지역이름[정점.정점]}: ${정점.거리}`));
console.log('-------------------');
}
return 거리;
}
const 그래프 = [
[0, 2, 5, 1, Infinity, Infinity],
[2, 0, 3, 2, Infinity, Infinity],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, Infinity],
[Infinity, Infinity, 1, 1, 0, 2],
[Infinity, Infinity, 5, Infinity, 2, 0],
];
const 시작정점 = 0;
const 최단거리 = dijkstra(그래프, 시작정점);
const 지역이름 = ['서울', '원주', '포항', '수원', '대전', '여수'];
console.log(`시작 정점(${지역이름[시작정점]})에서 다른 모든 정점까지의 최단 거리:`, 최단거리);-
인접 정점, 가중치 두 개를 객체화, 최소힙의 삽입
-
루트 노드에서는 항상 최소 가중치를 가진 정점이 저장 => 루트 노드값을 빼서 방문 처리를 한 후 다시 방문 중인 정점과 인접한 정점, 가중치를 객체화시켜서 최소힙에 삽입하는 과정을 반복
-
시간복잡도 : O(V log V + E), E는 간선의 수, V는 정점(노드)의 수
-
힙에 삽입하는데 O(log V) 시간이 소요되며, 최소 힙을 유지하는 과정은 모든 노드에 대해 이루어지므로 O(V log V) 시간이 소요
-
각 노드를 한 번씩만 방문하며, 각 노드에 대해 연결된 모든 간선을 탐색,따라서 이 과정의 시간 복잡도는 O(E)
= 따라서 시간복잡도는 O(V) + O(V log V) + O(E) = O(V log V + E)
✅ CS 질문
❓ Queue vs Priority queue를 비교해서 설명해주세요
Queue 자료구조는 시간 순서상 먼저 집어 넣은 데이터가 먼저 나오는 선입선출 구조롤 저장하는 형식이고, 우선순위큐는 들어간 순서에 상관없이 우선순위가 더 높은 데이터가 먼저 나온다.
시간복잡도 : Queue => enq O(1) deq O(1)
시간복잡도 : Priority Queue => push O(logN) pop O(logN)
❓ Priority Queue에 대해서 설명해주세요
우선순위큐는 가장 우선순위가 높은 데이터를 먼저 꺼내기 위해 고안된 자료구조입니다. 우선순위 큐를 구현하기 위해서 일반적으로 힙을 사용합니다. 힙은 완전이진트리를 통해서 구현되었기 때문에 우선순위 큐의 시간복잡도는 O(logn)입니다.
❓ Heap에 대해서 설명해주세요
완전 이진 트리 기반의 자료구조로 여러개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조
❓ Max Heap과 Min Heap에 대해서 설명해주세요
최대힙(Max Heap) : 부모노드의 키 값이 자식 노드의 키값보다 크거나 같은 완전 이진 트리
최소 힙(Min Heap) : 부모노드의 키값이 자식 노드의 키값보다 작거나 같은 완전이진트리
❓ Heap Push과정의 시간복잡도 대해서 설명해보세요
Heap tree의 높이는 logN이다. push()를 했을 때, 스왑하는 과정이 최대 logN번 반복되기 때문에 시간 복잡도는 O(logN) 이다.
❓ Heap Pop과정의 시간복잡도에 대해서 설명해보세요
pop()을 했을 때, 스왑하는 과정이 최대 logN번 반복되기 때문에 시간 복잡도는 O(logN)이다.
❓ 힙정렬이란?
최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다.
❓ 힙정렬의 과정에 대해서 설명해주세요
정렬해야 할 n개의 요소들로 최대 힙(완전 이진 트리 형태)을 만든다. 이후 내림차순을 기준으로 정렬하고 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장하면 된다. 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 된다.